纖維金屬混雜層合板拉伸強度分析

姜舜，趙耀

（華中科技大學船舶與海洋工程學院，湖北武漢 430074）

0 引言

纖維金屬混雜層合板（Hybrid fibre-metal laminates，FML）是由纖維增強樹脂層與金屬薄層交替粘接而成的1種新型結構材料，如圖1所示。其既具有傳統玻璃鋼的輕質、高強度、優越的抗疲勞和耐環境的性能［1－3］，同時相比于相應的單一輕金屬合金更耐疲勞。其優點是能像常規金屬合金薄板那樣進行處理和加工［4－8］，同時具備玻璃纖維和輕金屬的材料特性。FML中纖維層的各向異性特性為結構的可設計性創造了條件，即通過改變層合板各單層的纖維方向，鋪層順序，金屬層厚度來滿足結構強度和剛度的方向性要求，因此，在船舶制造及海洋工程和航空領域得到了越來越廣泛的應用。

考慮到纖維金屬混雜層合板在船舶建造領域的應用，以及其在大型復雜船舶結構有限元分析的可靠性問題。本文在層合板理論方法的基礎上，對纖維金屬混雜層合板的解析解進行擴展，使其能適用于纖維金屬混雜層合板，并利用有限元對纖維金屬混雜非對稱層合板進行數值分析，并與單向拉伸條件下的試驗值比較，認為有限元計算能滿足工程計算的要求;同時，討論了鋪層方式、金屬層厚度以及金屬層材料屬性對拉伸強度的影響，為大型復雜結構的有限元分析提供有益的參考。

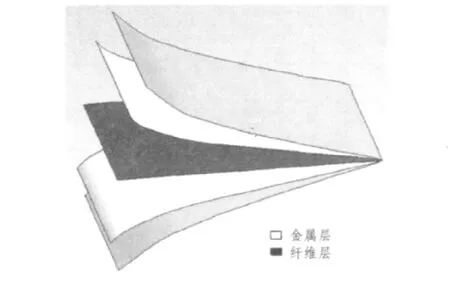
圖1 纖維金屬層合板FMLFig.1Hybrid fibre-metal laminates

1 層合板理論解的擴展

由于纖維金屬混雜層合板中金屬層的存在，金屬彈塑性應力－應變關系與玻璃纖維的本構關系的差異，需要對經典層合板理論進行擴展以適用于FML。同時，基于非對稱層合形式，根據計算層合板非中面剛度系數的方法進一步擴展層合板理論得到非對稱層合板剛度系數。

1.1 含金屬的層合板剛度矩陣

基于彈性力學薄板理論來討論層合板的應力和應變關系，即層合板的剛度。首先，對于一般正交各向異性層合板面內載荷作用在材料主應力方向，得到不考慮溫度因素影響時的一般層合板的廣義力和廣義應變關系［1］，即:

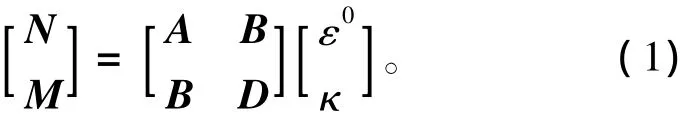
式中:N和M分別為層合板的單位長度的內力和內力矩;ε0和κ為中面應變和中面扭曲率;A，B，D分別稱為面內剛度矩陣、耦合剛度矩陣和彎曲剛度矩陣。當考慮有金屬層的存在，展開形式增加了金屬層剛度矩陣，即:

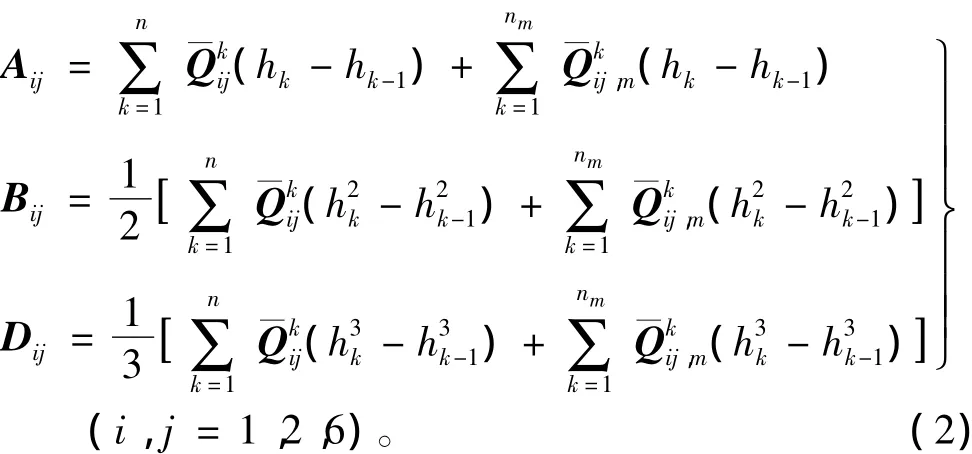
式中:hk和hk－1為第k層上下表面的z坐標值，如圖2所示;Qij，m為金屬層的剛度矩陣。

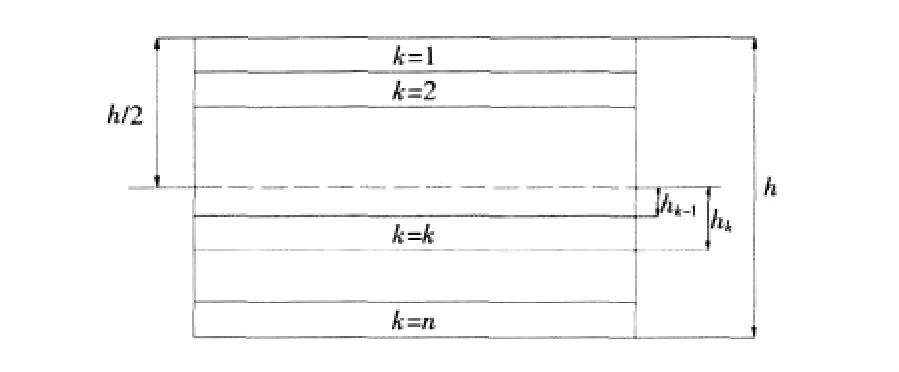
圖2 具有n個單層的層合板Fig.2Laminates with n layers

當金屬層擴展到層合板理論后，在分析FML時，金屬層的彈塑性關系也需要考慮。金屬層具有雙線性特征的應力－應變關系［8］，并且金屬的屈服遵守VonMises屈服準則，當金屬層等效應力達到屈服強度σy后，金屬層的總應力值和總應變值都可表示為:

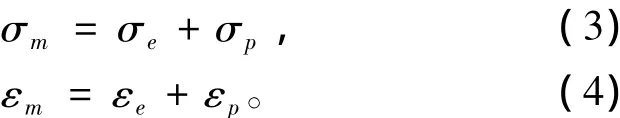
1.2 非對稱層合板的剛度矩陣

以上討論層合板剛度時，都將參考坐標系原點取在層合板厚度方向的幾何中心上，得到的是中面剛度系數。但是實際的工程結構往往采用的是不對稱的層合板鋪設形式，因此，本文又進一步對經典層合板進行擴展，利用計算非中面剛度系數，將每一層板看成偏離層合板中面的特殊層合板，此時層合板非中面剛度系數矩陣可表示為:

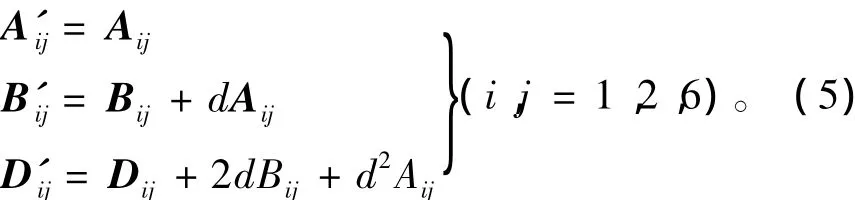
式中，d為假設面板中面到參考坐標軸的距離。

2 有限元與理論解結果對比

本文使用通用有限元結構分析系統對纖維金屬混雜非對稱層合板在承受單向受拉的情況下進行數值分析，驗證擴展的層合板理論解正確性。選取具有4個節點且每個節點有6個自由度的SHELL181單元［9］來模擬，鋪層形式為［Al/0/－45/45/90］，Al即金屬鋁層厚度為0.5 mm，其余各FRP層厚度為0.125 mm。其中，Al層為鋁合金材料，E=72 GPa，ν=0.33，FRP層為碳纖維增強復合材料，其單層屬性如表1所示。

以面內載荷100 N/mm作用在尺寸為25 mm× 100 mm的幾何模型上，網格劃分、約束條件、受力狀況如圖3所示。

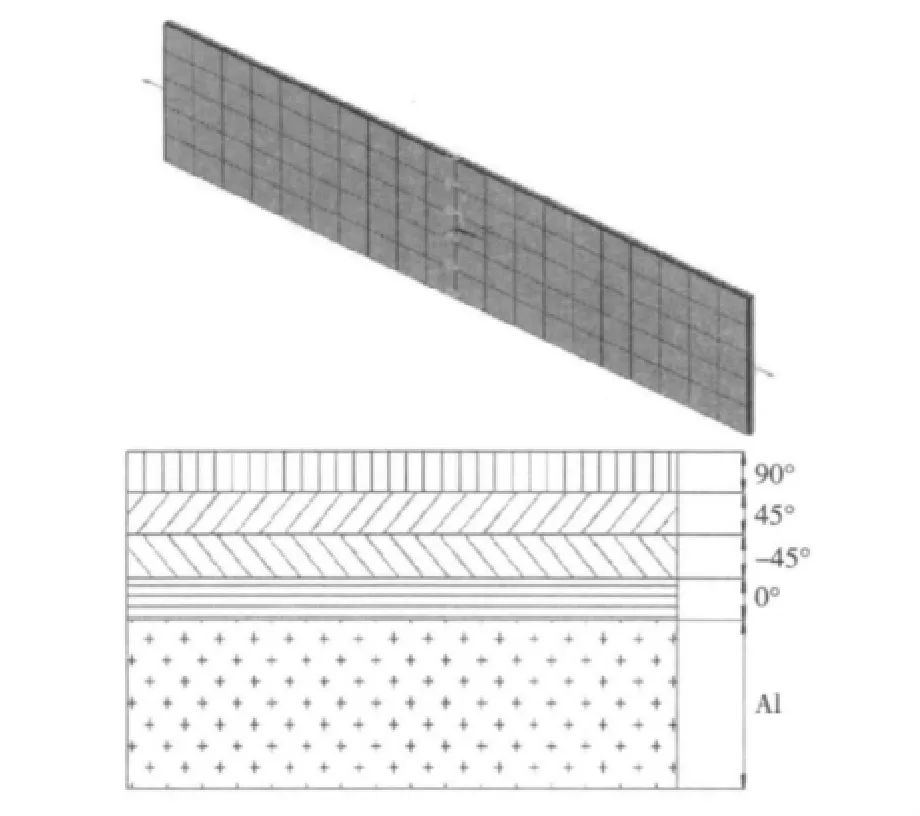
圖3 有限元計算模型Fig．3The finite element model

通過擴展的層合板理論解和數值計算結果列于表2，經過對比可以發現，數值計算得到的各層應力值和理論解相符。圖4和圖5分別顯示了數值計算中X和Y方向的應力計算在不同層內的分布情況。

由圖4可知，由于FML板為非對稱層合板，在載荷作用下，板發生了翹曲變形。分析變形產生的原因是:混雜層合板各層的材料屬性各異，承受同一拉載荷時應力和應變關系不一致，導致一側變形較另一側變形大最終反映在整體結構上就產生了翹曲變形形式。研究纖維金屬混雜層合板的變形特性，有助于掌握變形規律，從而實現對變形的控制和利用，以得到特殊工藝曲面，應用于工程實踐。

圖5表示FML板X方向應力在厚度的分布情況，由于纖維不同方向的彈性模量隨鋪設角度的變化而不同，因此應力在受拉的條件下的響應也不同。X方向最大應力位置都出現在FML的中心并向兩端遞減。經過2種方法所得結果的比較可以發現，擴展的理論解與有限元數值計算結果吻合得相當好，證明了有限元數值計算在描述纖維金屬混雜層合板拉伸特性方面具有相當的可靠性，使其成為計算大型復雜結構的重要依據。

圖5 FML板X方向應力值分布Fig．5The stress in X direction

3 計算實例分析

3.1 FML單向拉伸試驗的數值模擬

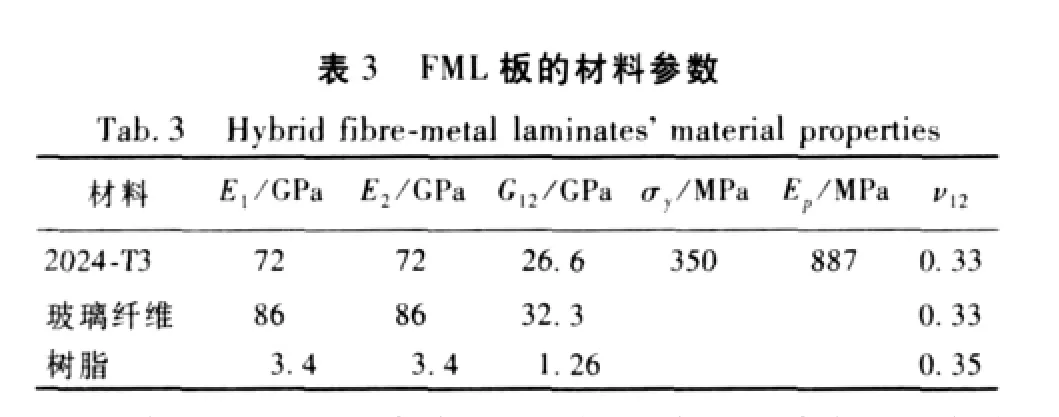
數值計算和理論值的比較取得了很好的吻合結果，通過數值模擬FML拉伸試驗進一步驗證擴展層合板的理論正確性，選取文獻［10］中的混雜層合板結構。為真實模擬試驗，完全依據文獻提供的構件尺寸，計算模型的鋪層順序為［Al/0/90/90/0/Al］，FRP層厚度為0.146 mm，Al層厚度為0.489 mm，板尺寸為305 mm×25.5 mm，FML板材料參數如表3所示。

運用通用有限元結構分析系統得到模擬試驗的拉伸應力－應變曲線如圖6所示，根據有限元計算繪制的應力－應變關系與試驗結果的對比可以發現:在單軸拉伸載荷作用下，FML層合板拉伸強度表現出雙線性關系。在初始線性階段，Al層和FRP層共同承載外力載荷。當應力達到267 MPa時，Al層達到屈服應力，Al層承載能力逐漸下降，此時應力－應變曲線即開始偏離原線性路徑，應力進行了重新分布，這時載荷主要由FRP層承載。可以發現，在相當長的加載過程中，數值計算結果和試驗值吻合得非常好，只有在加載的后端由于FRP層隨著載荷的增加逐層失效，計算結果與試驗值出現分離，這一現象也與選擇的殼單元有關，并沒有考慮層間應力在抗拉強度時的作用。

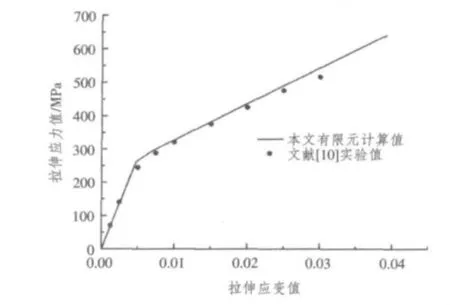
圖6 模擬拉伸試驗的應力－應變曲線Fig.6Stress-strain curves of FML under uniaxial tensile loading longitudinal

3.1.1 鋪層方式對拉伸強度的影響

為研究鋪層方式對纖維金屬混雜層合板拉伸應力－應變的影響，數值計算了θ分別為0°，15°，30°，45°，60°，75°和90°時的尺寸為300 mm×30 mm板拉伸應力－應變的關系。鋪層方式為［Al/θ/θ/Al/θ/θ/Al］，FRP厚度0.15 mm，Al層單層厚度0.5 mm，材料參數參照文獻［10］，加載方式均采用應力加載方式，計算結果如圖7所示。

由圖7可見，隨著角度的變化彈性階段的曲線趨于一致，只有在達到屈服點的位置有所差異。塑性部分的變化在0°～45°范圍內是隨著角度的增加而曲線的斜率逐漸降低，45°～90°范圍內角度的增加曲線變化范圍很小。曲線的趨勢在45°前后產生截然不同的特性，分析此現象出現的原因是在小角度范圍FML主要由剛度較大的FRP層承載，而在大角度范圍初始階段Al層和FRP層剛度相近，共同承受載荷因此應力很快達到屈服應力，應力也在Al層進入塑性后重新分布，導致剛度下降較快。

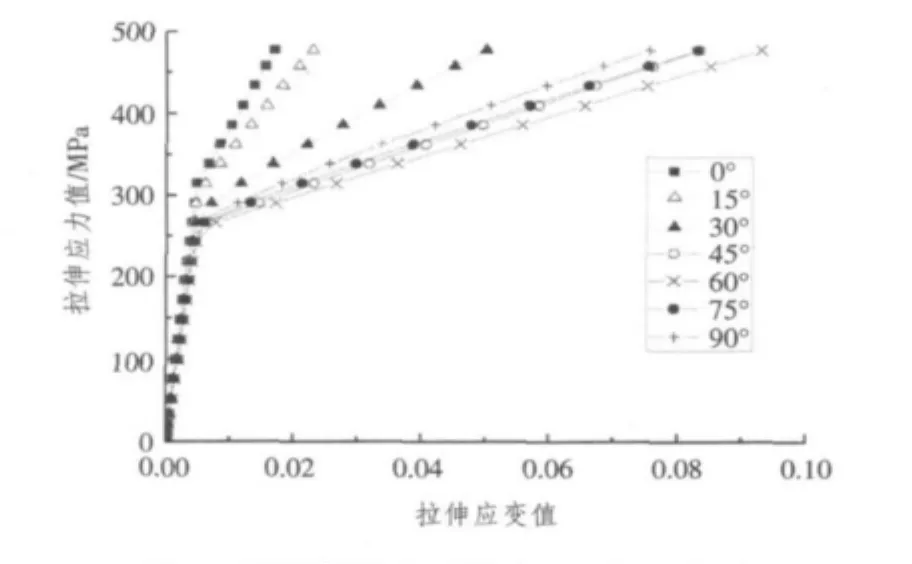
圖7 不同鋪層方式的應力－應變關系Fig.7Stress-strain curves in different angle ply

3.1.2 正交鋪層方式對拉伸強度的影響

為了討論正交鋪層方式對纖維金屬混雜層合板拉伸應力－應變的影響，本文選取了3組纖維層相互垂直鋪設［Al/0/90/Al/90/0/Al］，［Al/30/－60/Al/－60/0/Al］，［Al/45/－45/Al/－45/45/Al］時板拉伸應力－應變的關系，計算結果如圖8所示。

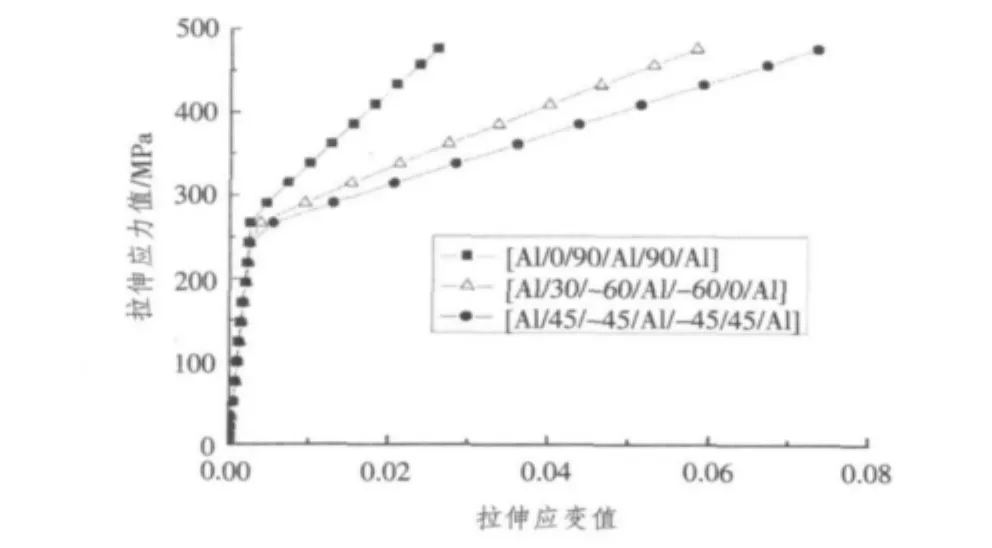
圖8 不同正交鋪層方式的應力－應變關系Fig.8Stress-strain curves in different orthogonal ply

分析計算結果，FRP層都是采用相互正交的鋪層方式，雖然在屈服點位置上非常接近，然而繼續加載后，隨著正交角度的改變，載荷方向的抗拉模量也隨之規律變化，不同的正交角度產生了不同的應力－應變特征，［Al/45/－45/Al/－45/45/Al］鋪層方式的FML在金屬層進入塑性段后剛度下降最快，而［Al/ 0/90/Al/90/0/Al］方式下剛度下降最慢。

3.1.3 金屬厚度對層合結構的影響

為了研究金屬層厚度對纖維金屬混雜層合板拉伸應力－應變的影響，分別數值計算了Al層厚度為0.2～0.5 mm的FML拉伸應力－應變關系。鋪層方式為［Al/0/90/90/0/Al］，計算結果如圖9所示。

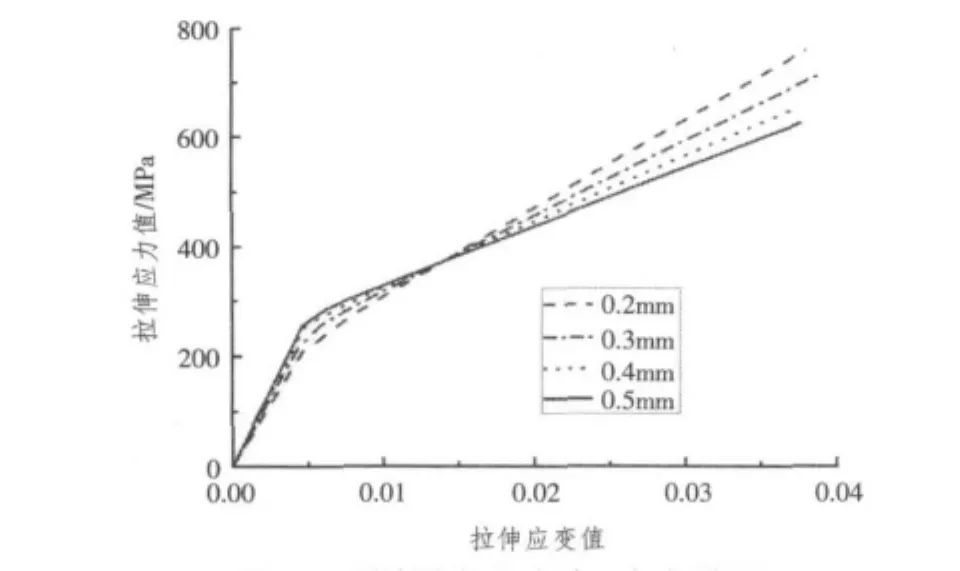
圖9 不同厚度的應力－應變關系Fig.9Stress-strain curves in different thickness of metal

圖9所示，隨著Al層厚度的增加，屈服應力點成正比例增大。由此可見，金屬層的厚度對FML的拉伸強度的影響是很大的，而且是成比例的增加。因此，可以通過增加金屬層的厚度來提高纖維金屬混雜層合板的整體拉伸強度。

3.1.4 金屬層材料屬性對層合結構的影響

考察不同金屬材料屬性對纖維金屬混雜層合板拉伸應力－應變的影響，計算了金屬層材料參數分別為Em=70 GPa，90 GPa，110 GPa和130 GPa時FML拉伸應力－應變的關系，鋪層方式為［M/0/0/0/0/M］，M代表金屬層，其厚度為0.5 mm，計算結果如圖10所示。

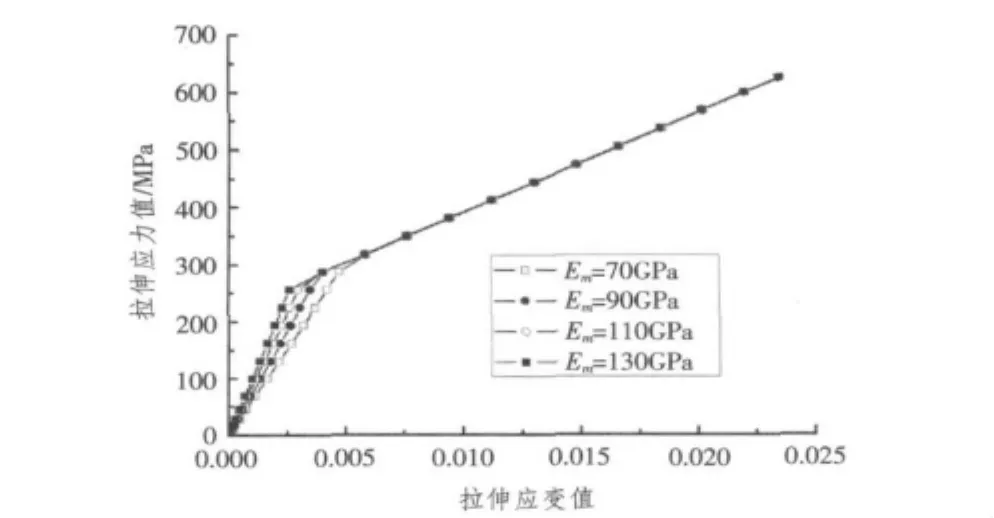
圖10 不同金屬材料的應力－應變關系Fig.10Stress-strain curves in different properties of metal

從圖10中可以看到，由于金屬層的彈性模量的增大，發生屈服應力值也隨之增大，當FML的金屬層進入塑性之后，層合板的應力－應變關系趨于一致，表現出相同的應力－應變特征。

4 結語

基于經典層合板理論，對纖維金屬混雜非對稱層合板的理論解進行了擴展，考慮了金屬層的彈塑性特征對層合板拉伸特性的影響，經過與數值計算結果的比較，證明該擴展形式能較好地模擬纖維金屬混雜非對稱層合板特性。同時，進一步利用有限元計算和對稱層合板拉伸試驗結果很好的吻合，保證了纖維金屬混雜層合板拉伸強度分析的正確性。

本文還討論了鋪層方式和金屬層板厚對FML的影響，并且得到以下結論:

1）隨著鋪層角度的變化，FML拉伸彈性階段的性質趨于一致，但是在達到屈服點的位置有所差異;塑性部分的變化在0°～45°范圍內是隨著角度的增加而曲線的斜率逐漸降低，45°～90°范圍內角度的增加曲線變化范圍很小。因此，不同的鋪層方式對FML拉伸強度的影響是不同的。

2）不同的正交角度產生了不同的應力－應變特征，屈服點位置上非常接近，然而繼續加載后［Al/45/－45/Al/－45/45/Al］鋪層方式的FML在金屬層進入塑性段后剛度下降最快，而［Al/0/90/Al/90/0/Al］方式時剛度下降較慢。

3）隨著Al層厚度的增加，屈服應力成正比例增大。金屬層的厚度對FML的拉伸強度的影響是很大的，而且是成比例的增加。

4）由于金屬層的彈性模量的增大，發生屈服應力值也隨之增大，當FML的金屬層進入塑性之后，層合板的應力－應變關系表現出相同的特征。

［1］矯桂瓊，賈普榮．復合材料力學［M］．西安:西北工業大學出版社，2008．

［2］布賴恩，哈里斯．工程復合材料［M］．陳祥寶，張寶艷，譯．北京:化學工業出版社，2004．

［3］趙美英，陶梅貞．復合材料結構力學與結構設計［M］．西安:西北工業大學出版社，2007．

［4］GUACAI W，YANG J M．The mechanical behavior of gLARE laminates for aircraft structures［J］．JOM，2005，57:1－72．

［5］REYES G，CANTWELL W J．The mechanical properties of fibre-metallaminatesbasedonglassfibre-reinforced polypropylene［J］．Composites Science and Technology，2000，50:1085－1094．

［6］SINKE J．Manufacturing of GLARE parts and structures［J］．Applied Composite，2003，10:293－305．

［7］KAWAI M，MORISHITA M，TOMURA S，TAKUMIDA K．Inelastic behaviorandstrengthoffibre-metalhybrid composite:GLARE，International Journal of mechanical sciences，1998，40:183－198．

［8］彭文杰．復合材料層合結構極限強度預測方法及分層應力最小化研究［D］．武漢:華中科技大學，2009．

［9］張朝暉．ANSYS 11.0結構分析工程應用實例解析［M］．北京:機械工業出版社，2009．

［10］WU G，YANG J M．Analytical modelling and numerical simulation of the nonlinear deformation of hybrid fibremetal laminates［J］．Modelling and simulation in materials science and engineering，2005，13:413－425．