非理想條件下三軸磁通門傳感器誤差修正方法

周榕軍，劉大明，洪澤宏，趙永，周國華

（1．海軍工程大學電氣與信息工程學院，湖北武漢430033; 2．中國人民解放軍91003部隊，海南三亞 572016）

0 引言

三軸磁通門傳感器所具有的高分辨率和良好的魯棒性使其廣泛應用于民用和軍事領域［1－2］，如導航系統、磁探傷、艦船磁場測量。就理論上而言，磁通門傳感器的3個測量軸必須相互正交。然而在實際制造過程中，由于制造工藝和加工水平的限制，3個測量軸不可能做到絕對正交。此外，為方便磁場測量數據的處理，通常需將磁傳感器水平放置，但在磁傳感器的實際使用過程中，很難使磁傳感器絕對水平地放置。三軸磁傳感器本身所固有的上述特點都給磁場測量帶來了較大的測量誤差，從而難以應用于磁場測量精度要求較高的場合。因此，許多工作者對三軸磁傳感器進行了研究，文獻［3］采用共軛梯度法校正了三軸磁傳感器正交性誤差，文獻［4－5］分析了三軸磁傳感器非理想放置時數據處理方法及其水平修正方法，文獻［6－7］基于最小二乘多項式曲線擬合原理提出了磁傳感器非線性誤差的消除方法。在實際磁場測量過程中，非正交誤差和非水平誤差是同時存在的，而過去通常將非正交誤差和非水平誤差進行獨立校正，當校正其中之一時需假設另1個誤差不存在，因而校正較為粗略。本文基于微分進化算法提出1種非正交和非水平誤差聯合修正方法。

1 三軸磁傳感器測量模型

假設存在非正交誤差和非水平誤差的三軸磁傳感器狀態為非理想狀態，3個測量軸分別為ox，oy和oz，三軸輸出值分別為Bx，By和Bz。不存在非正交誤差和非水平誤差的三軸磁傳感器狀態為理想狀態，3個測量軸分別為oxt，oyt和ozt，三軸輸出值分別為Bxt，Byt和Bzt，且使ox與oxt位于同1個垂直平面內。如圖1所示，α1為測量軸x與測量軸xt之間的夾角，α2為測量軸x與測量軸yt之間的夾角，α3為測量軸x與測量軸zt之間的夾角。為方便，同樣令β1，β2和β3分別為測量軸y與測量軸xt，yt，zt之間的夾角，γ1，γ2，γ3分別為測量軸z與測量軸xt，yt，zt之間的夾角。

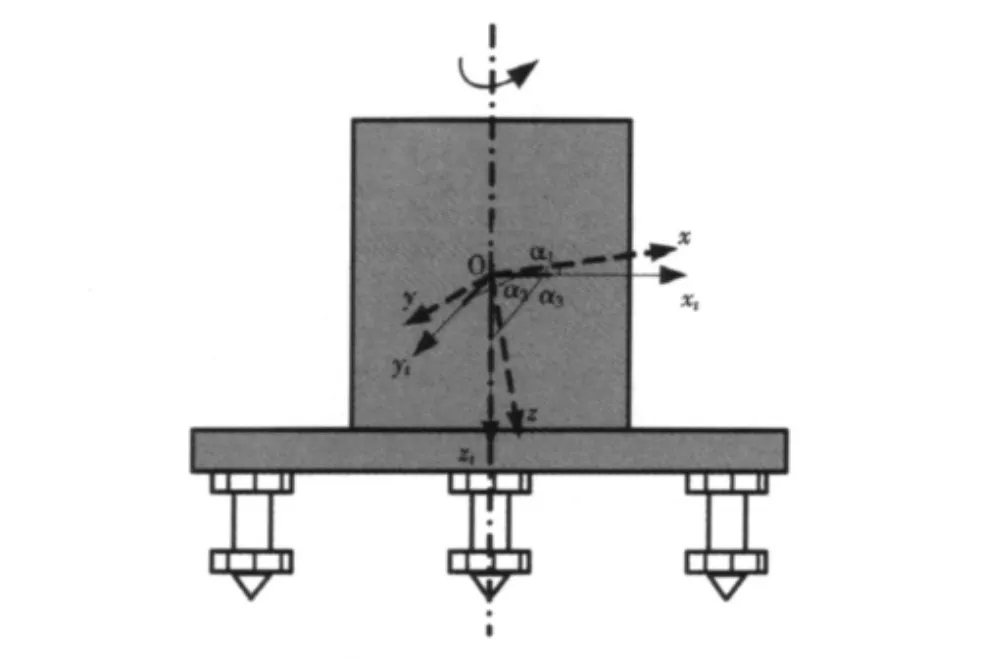
圖1 非理想狀態與理想狀態磁傳感器測量軸關系示意圖Fig.1The sketch map of the relationship of measurement axis between the ideal and non-ideal magnetic sensor

由上述理想狀態下磁傳感器與非理想狀態下磁傳感器測量軸之間關系可知，非理想狀態下磁傳感器三軸輸出值可表示為

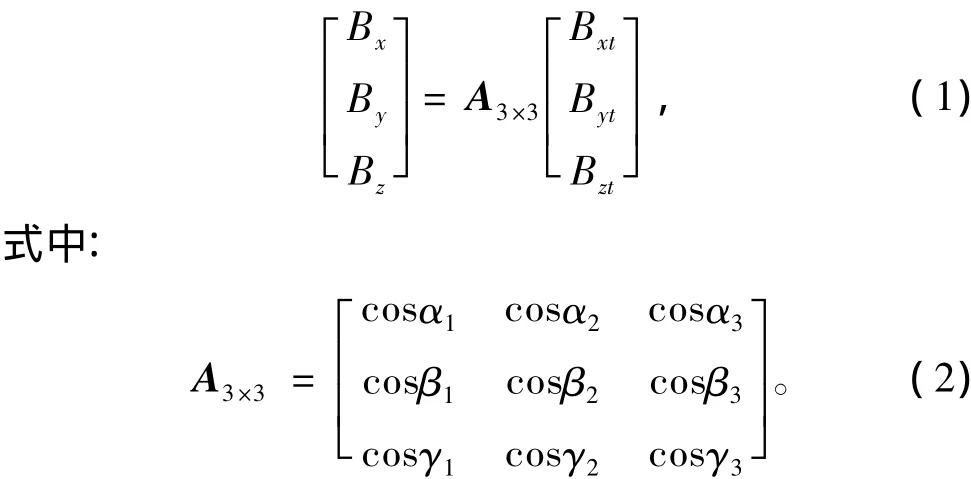
可以看出，若已知轉化矩陣A3×3，則可利用非理想狀態下磁傳感器三軸測量值求出理想狀態磁傳感器三軸測量值，

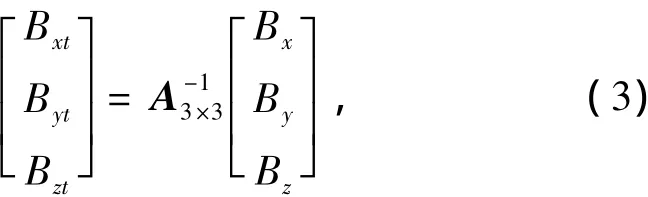
從而消除非理想狀態磁傳感器三軸測量值中的非正交誤差和非水平誤差。

式中:a1，b1，b2，c1，c2為轉化矩陣參數，且都小于1。對于三軸磁傳感器而言，其可滿足一定的正交度和水平度要求，因而可將轉化矩陣A3×3中參數范圍進一步縮小。

2 基于微分進化算法的轉化矩陣參數求解

在僅有地磁場作用的同一測量點處，使磁傳感器繞中軸線作旋轉運動，如圖1所示。每旋轉一定角度就記錄下磁傳感器三軸輸出值，經n次旋轉則可得到n組磁場測量數據，分別記為，其中i= 1，2，…，n。顯然，若磁傳感器不存在非正交和非水平誤差，則磁傳感器z軸輸出值Bzt和三軸總量值Bxt2+ Byt2+Bzt2均恒定不變。根據此特征，可建立以轉化矩陣參數為未知量的優化模型:

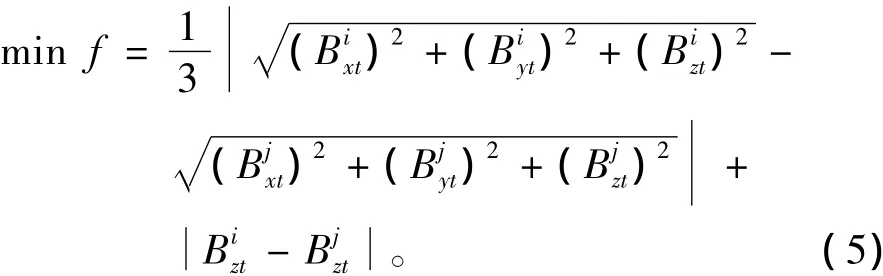
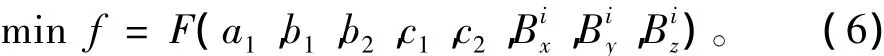
式中:函數關系F由式（3）～（5）確定。不難看出，該優化模型是一個非線性優化問題，必須采用優化算法來對其進行求解，以得到轉化矩陣參數。鑒于隨機類優化算法中微分進化算法（Differential Evolution，DE）簡單且有效，采用微分進化算法來求解上述非線性優化問題。

微分進化算法的基本思想是對種群中的每個個體i，從當前種群中隨機選擇3個點，以其中1個點為基礎，另2個點為參照作1個擾動，所得點與個體i交叉后進行“自然選擇”，保留較優者，實現種群的進化［8－9］。

不妨將優化參數a1，b1，b2，c1，c2記為向量形式的自變量［x1，x2，x3，x4，x5］，采用微分進化算法優化求解上述模型時，具體步驟為:

1）初始化進化參數。設置種群規模N，交叉概率Pc，交叉因子Fw，進化次數t，自變量參數閾值lb和ub。隨機生成初始種群X（0）={X1（0），X2（0），…，XN（0）}，其中

2）個體評價。計算每個個體Xi（t）的目標函數值F（Xi（t））。

3）交叉繁殖。對種群中的每個個體Xi（t），隨機生成3個互不相同的隨機整數rs（1≤rs≤N）和隨機整數jr（1≤jr≤n），按下式進行計算:

5）如果滿足迭代結束要求，則輸出種群中具有最小目標函數值的個體作為最優解。否則返回步驟2）。

3 傳感器實驗

將試驗磁傳感器置于低磁實驗室內某測量點處，并將磁傳感器繞中軸線按順時針等間隔30°旋轉1周，記錄得到了12組磁場測量數據，實驗示意圖見圖2。

圖2 傳感器實驗示意圖Fig.2The sketch map of the magnetic fluxgate sensor experiment

采用微分進化算法來優化求解轉化矩陣參數時，微分進化算法中具體參數為:參數數目m=5，種群規模N=25，交叉概率Pc=1，交叉因子Fw=0.85，參數變化范圍lb=－0.2，ub=0.2，迭代次數t=500。

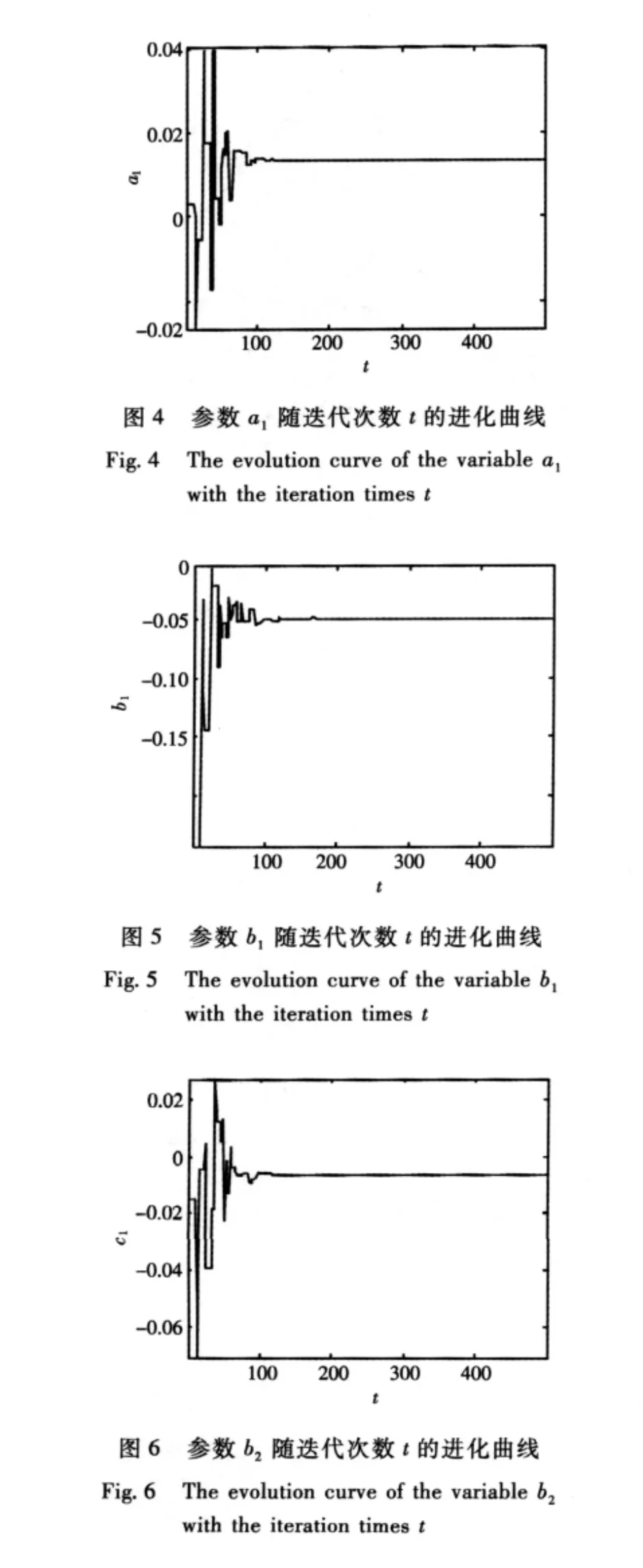
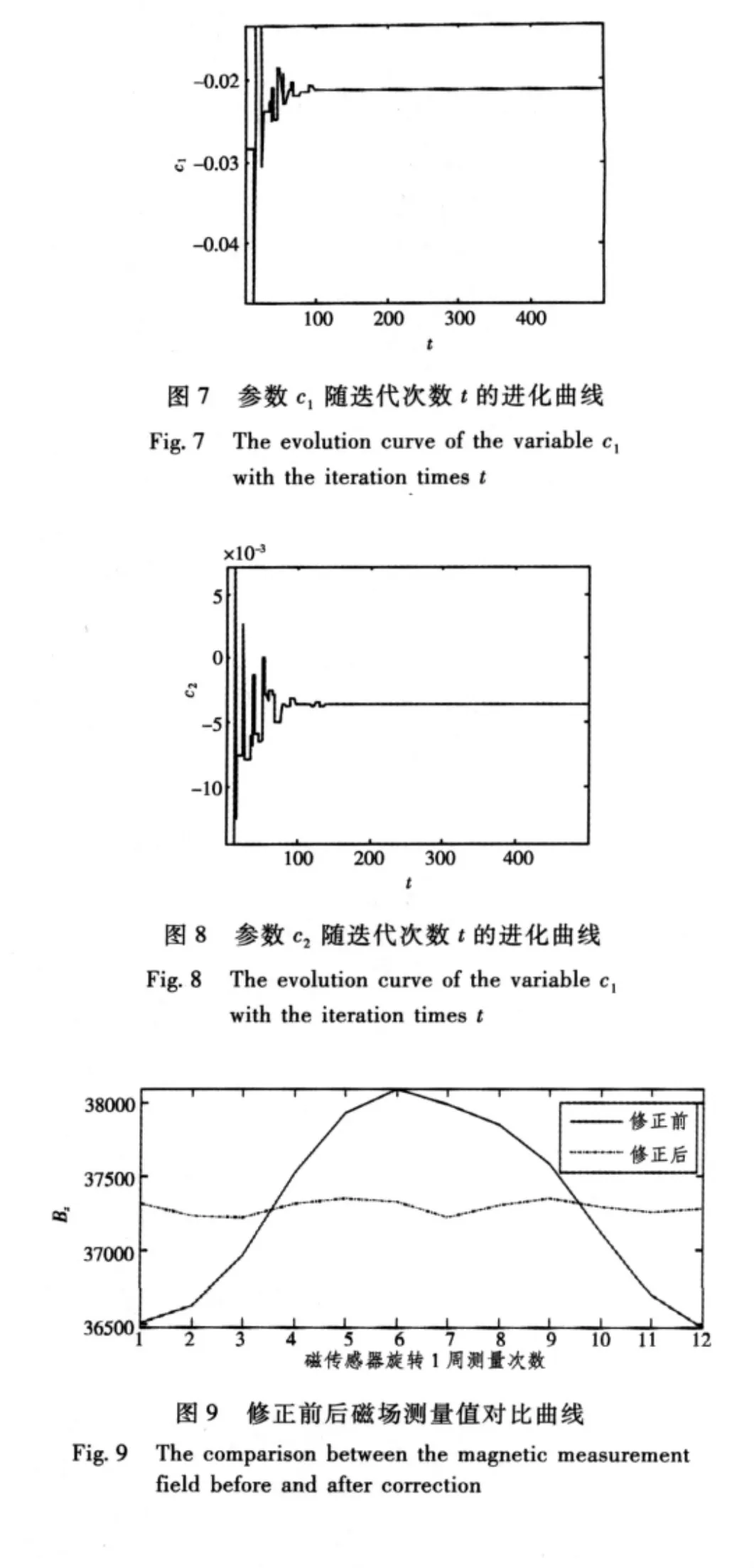
基于微分進化算法求解轉化矩陣參數的過程如圖3～9所示，所求得的參數為a1=0.013572，b1= 0.000115，b2=－0.006312，c1=－0.021201，c2=－0.003657。圖3給出了目標函數值隨迭代次數的變化關系。可以看出，經過100次迭代后目標函數值已基本穩定。圖4～8分別給出了轉化矩陣參數a1，b1，b2，c1和c2隨迭代次數的變化關系。可以看出，轉化矩陣參數都可較快收斂到穩定值。圖9給出了三軸磁傳感器在修正前z軸輸出值與修正后z軸輸出值的對比圖。可以看出，通過修正可顯著改善三軸磁傳感器的測量精度。

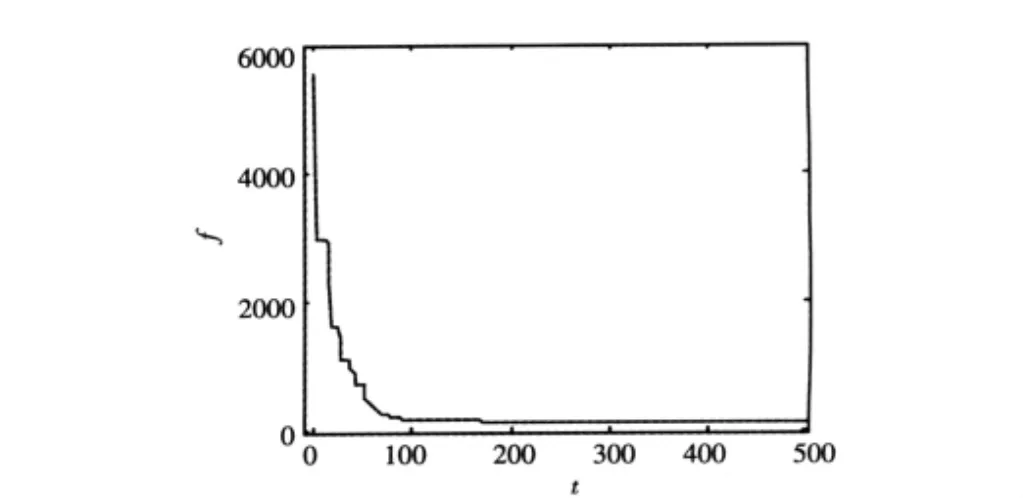
圖3 目標函數值f隨迭代次數t的進化曲線Fig.3The evolution curve of the object function f with the iteration times t

4 結語

本文提出了基于微分進化算法的三軸磁通門傳感器非正交誤差與非水平誤差聯合修正方法，與過去將非水平誤差和非正交誤差獨立進行修正相比，該方法具有一定的優勢。三軸磁通門誤差消除實驗表明了該方法可在一定程度上消除非正交性和非水平放置給測量帶來的影響，從而顯著改善磁場測量精度，具有一定的實用意義。

［1］潘啟軍，馬偉明，趙治華，等．磁場測量方法的發展及應用［J］．電工技術學報，2005，20（3）:7－13．

PAN Qi-jun，MAWei-ming，ZHAOZhi-hua，etal．Development and application of measurement method for magnetic field［J］．Transactions of China electrotechnical society，2005，20（3）:7－13．

［2］涂疑，郭文生，曹大平．磁通門傳感器的應用與發展［J］．水雷戰與艦船防護，2002，（1）:36－38．

TU Yi，GUO Wen-sheng，CAO Da-ping．Application and development of magnetic fluxgate sensors［J］．Mine war and ship protection，2002，（1）:36－38．

［3］胡海濱，林春生，龔沈光．基于共軛次梯度法的非理想正交三軸磁傳感器的修正［J］．數據采集與處理，2003，18 （3）:88－91．

HUHai-bin，LINChun-sheng，GONGShen-guang．Correction of incompletely orthogonal three axial magnetic sensor by conjugated approximate gradient algorithm［J］．Journal of Data Acquisition＆Processing，2003，18（3）:88－91．

［4］肖昌漢，何華輝．三分量磁傳感器非理想放置時磁場數據的分析方法［J］．海軍工程學院學報，1996，76（3）: 7－12．

XIAO Chang-han，HE Hua-hui．An analysis method of magnetic field data from the non-idealy placed 3 axial magnetometer sensor［J］．Journal of naval academy of engineering，1996，76（3）:7－12．

［5］閆輝，肖昌漢，張朝陽．三分量磁通門傳感器水平修正方法［J］．電子測量與儀器學報，2006，20（6）:90－93．

YAN hui，XIAO Chang-han，ZHANG Zhao-yang．Horizontal calibration to triaxial fluxgate magnetometer［J］．Journal of electronic measurement and instrument，2006，20（6）:90－93．

［6］郭志友，孫慧卿．磁傳感器的非線性誤差修正技術［J］．傳感器技術，2004，23（5）:54－56．

GUO Zhi-you，SUN Hui-qing．Technology of non-linearity error revision on magnetic sensors［J］．Journal of transducer technology，2004，23（5）:54－56．

［7］孫慧卿，郭志友．傳感器的誤差補償技術［J］．傳感技術學報，2004，3（1）:90－92．

SUNHui-qing，GUOZhi-you．Technologyoferror compensation on sensors［J］．Journal of sensor technology，2004，3（1）:90－92．

［8］陽明盛，羅長童．最優化原理、方法及求解軟件［M］．北京:科學出版社，2006．140－151．

YANGMing-sheng，LUOChang-tong．Optimization principle，algorithm and solution softwares［M］．Beijing: Science Press，2006．140－151．

［9］STORN R．Differential evolution，a simple and effcient heuristic strategy for global optimization over continuous spaces［J］．Journal of Global Optimization，1997，11:341－359．