捷聯式慣導系統仿真器設計

王喜龍，程遠，吳汪洋

（1．海軍駐431廠軍代表室，遼寧葫蘆島125004;2．中國艦船研究院，北京 100192）

0 引言

計算機技術的飛速發展使得捷聯系統的設計與分析工作（特別是系統的誤差分析工作）可以首先在計算機進行，在此基礎上再進行系統的硬件（包括陀螺、加速度計與計算機等）及系統軟件（包括各種計算機算法及不同迭代周期的選擇等）的設計和選擇。但由于條件所限，在不能提供系統硬件的情況下為了進行捷聯慣導系統的研究，開發慣導仿真器是必不可少的。

1 捷聯慣導系統仿真器的實現

本文針對飛行器用捷聯慣性導航系統的工作環境進行仿真，其主要目的是仿真出符合實際慣導系統的誤差，捷聯慣導系統仿真器包括4個模塊:飛行軌跡發生器，慣性敏感元件仿真器（陀螺仿真器和加速度計仿真器），導航計算機仿真器和誤差處理器。仿真結構如圖1所示［1］。

1.1 飛行軌跡發生器［2－4］

飛行軌跡數據生成是為了測試驗證導航軟硬件系統實時計算性能而必需的輸入信號數據。對于捷聯慣導仿真系統，需要2類飛行軌跡數據:飛行姿態數據（姿態角、姿態角轉動速率）和飛行軌跡數據（位置、速度、加速度）。實際飛行時，這2類數據的變化是有關聯的。如果根據飛機模型和飛行力學原理，用數學的方法來產生一個與實際完全相符的飛行軌跡數據文件，將會因為各飛行軌跡量之間的耦合關系，使數學模型的建立非常復雜，甚至無法建立起精確的數學模型。

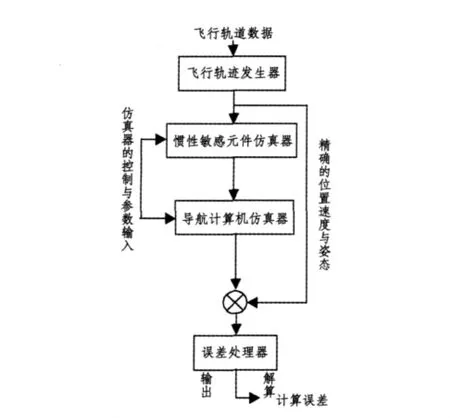
圖1 數字仿真器原理方框圖Fig．1Principle block diagram of digital simulation

為了簡化建模，認為2類數據按照各自獨立的規律變化，二者之間的變化沒有關系，這樣就可以很方便地用數學公式產生出任意時刻精確的理想飛行軌跡數據。測試用飛行軌跡數學模型的基礎是相互獨立的3個姿態角時間函數、3個位置時間函數。這樣計算生成的飛行軌跡雖然不是實際飛行軌跡，但可以很方便地得到任意時刻的精確測試用飛行軌跡數據，用來檢驗捷聯慣導系統仿真器的正確性和精度。

1.1.1 飛行姿態數據生成

設定飛行姿態角是隨時間變化的余弦函數（也可以根據需要設定為其他函數）:

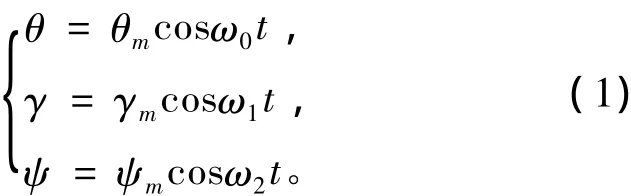
機體系相對于地理系的轉動角速率?在機體系中的投影為:

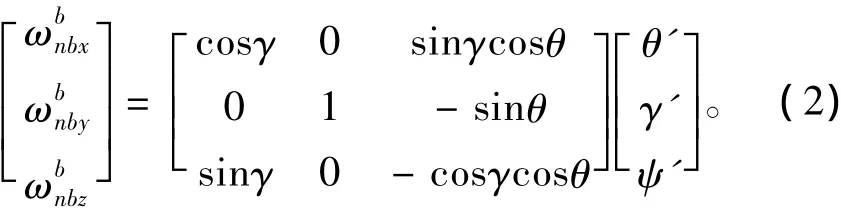
1.1.2 飛行軌跡數據生成

設定位置（緯度、經度、高度）的變化規律為時間的正弦函數（也可以根據需要設定為其他函數），并計算出位置的一階和二階導數:

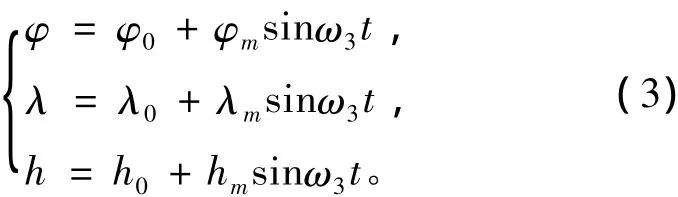
計算出地球直角坐標系中飛行載體位置所對應的直角坐標系R（x，y，z），并求直角坐標的一階和二階導數，

其中，R′為導航系相對于地球的速度在地球坐標系中的投影。

在地球系中的相對于地球加速度在導航系中的投影和在導航系中的相對于地球加速度在導航系中的投影為:

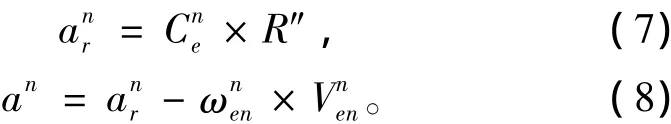
其中，R″為相對于地球加速度在地球系中的投影。

1.2 慣性敏感元件仿真器

慣性敏感元件仿真器給出陀螺與加速度計的仿真模型。當只研究計算機的算法誤差時，則不考慮敏感元件的誤差;當研究敏感元件的誤差時，其誤差也通過仿真器給出。

1.2.1 陀螺仿真器的數學模型［5－6］

職業教育主要培養面向企業一線具有較強實踐性和職業性的技能型人才，要求教師不僅具備專業理論知識，還需要有一定的實踐能力。近年來，隨著我國社會經濟發展，產業結構調整等新情況的出現，職業教育師資隊伍總量不足、培養機制不完善等，因此，有必要分析職院校“雙師型”教師隊伍建設存在的問題以及提出解決路徑。

理想角速率陀螺儀測量的是機體坐標系（b系）相對與慣性坐標系（i系）的轉動角速率在機體坐標系中的投影?。從飛行軌跡數據中，可以得到機體坐標系相對于導航坐標系（n系）的轉動角速率在機體坐標系中的投影。通過飛行軌跡數據中的水平速度、緯度、高度可以計算出導航坐標系相對于慣性坐標系的轉動角速率在導航坐標系中的投影，通過姿態角算出從導航坐標系到機體坐標系之間的轉換矩陣乘上轉換矩陣得到相加，得到陀螺儀模型的理想輸出。

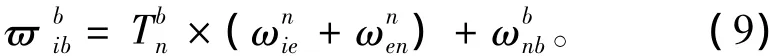
完整的陀螺模型包括理想輸出量、隨機誤差量（隨機常值誤差、白噪聲誤差、一階馬爾可夫過程誤差）、刻度因子誤差，用數學公式表示為:

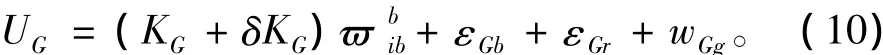
式中:UG為完整陀螺模型的輸出;KG為刻度因子; δKG為刻度因子誤差;為陀螺模型理想輸出;εGb為陀螺隨機常數誤差;εGr為陀螺一階馬爾可夫過程誤差;wGg為陀螺白噪聲誤差。

1.2.2 加速度計仿真器的數學模型［7－8］

完整的加速度計模型包括理想輸出量、隨機誤差量（隨機常值誤差、白噪聲誤差、一階馬爾可夫過程誤差）、刻度因子誤差，可用數學公式表示為:

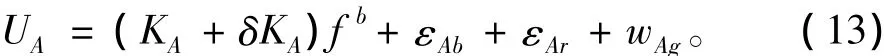
1.3 導航計算機仿真器

導航計算機的仿真可以根據系統對計算機的要求及現有的機載計算機的性能進行。在仿真中可以對計算精度、計算時間、計算字長及單精度與雙精度計算等方面取得必要的數據，以便選擇合適的機載計算機及計算機算法。

1.4 誤差處理器

由導航計算機仿真器計算出的帶誤差的導航參數與飛行軌跡發生器產生的精確導航參數進行比較，得出計算的位置、姿態、地速、高度等參數的導航誤差。可以通過誤差曲線圖分析仿真結果是否正確，完成全部的捷聯系統數字仿真器工作。

利用C語言設計的捷聯慣導系統仿真器已在微機上實現。仿真環境是在靜態條件下，選擇地理坐標系為數字平臺。在對飛行軌跡數據仿真的算法公式中:θ，λ和h分別為緯度、經度和高度;φ，γ和ψ分別為俯仰角、橫滾角和航向角。仿真過程中，式（1）和式（3）所涉及參數設定的缺省值為［9］:

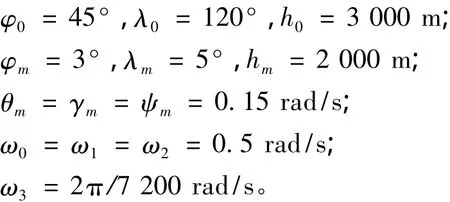
飛機位置、姿態角的誤差曲線圖分別如圖2～圖4所示。

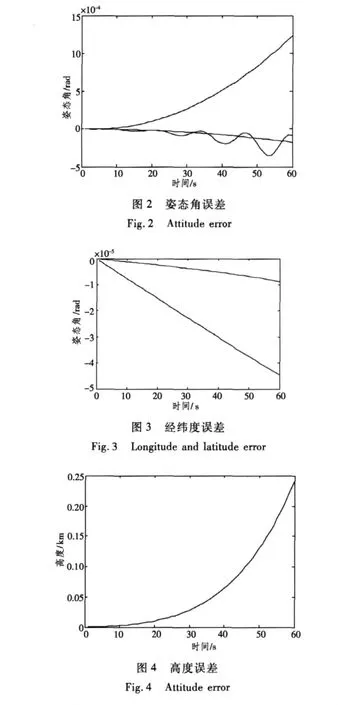
仿真結果表明，捷聯慣導仿真器工作正常，慣導的位置誤差、姿態誤差隨時間積累，長時間工作后慣導精度無法滿足導航或制導的精度要求。以上仿真誤差曲線是在陀螺儀與加速度計沒有誤差，也沒有初始對準誤差的理想條件下生成的捷聯慣導仿真誤差曲線，產生誤差的主要因素是計算誤差。可以看出，隨著時間的增長，誤差也在呈發散趨勢增長。因此，必須采取有效手段，對慣導系統進行修正，以提高導航精度。

2 結語

本文所設計的捷聯慣導系統仿真器利用面向對象的思想進行模塊分解，具有很強的擴展性。該仿真器大大縮短了從理論方案到實際應用之間的距離，為工程應用提供了一種全面觀察捷聯系統在不同應用條件下精度、性能的強有力的工具。結合不同的使用環境，可以對其中具體的模塊進行相應的重新設計。比如軌跡發生器仿真模塊、慣性敏感元件誤差模塊都可以依據系統具體的工作環境，對其中的各種參數或公式進行重新選擇，從而達到更加真實的仿真效果。

［1］陳哲．捷聯慣導系統原理［M］．北京:宇航出版社，1986．206－211．

［2］李麗娟，王琪，羅超．VC環境下捷聯慣導模擬器的開發［J］．應用科技，2006，33（3）:46－49．

［3］劉柱，高偉，曹潔．捷聯慣導系統仿真器的設計［J］．應用科技，2004，31（7）:40－42．

［4］LEE J G，PACK H W．Multiposition alignment of strapdown inertial navigation system［J］．IEEE Transactions on Aerospace and Electronic Systems，1993，29（4）:1323－1328．

［5］GAI E．The century of inertial navigation technology［J］．Aerospace Conference Proceedings，2000，11（3）:59－60．

［6］LOVREN N，PIEPER J K A．Strapdown inertial navigation system for flat-earch model［J］．IEEE Transaction on Aerospace and Electronic Systems，1997，33（1）:214－224．

［7］吳小蘭．易于實現的捷聯式慣性導航系統仿真［J］．彈箭與制導學報，2006，26（4）:89－91．

［8］黃金明，王立文，鄭淑濤．飛行模擬器綜合導航系統建模與仿真［J］．系統仿真學報，2006，18（s2）:665－668．

［9］趙玉霞．捷聯慣導系統仿真算法的研究及其實現［D］．大連:大連理工大學，2005．