一種新的變步長LMS算法

呂春英，敖 偉，張洪順

（重慶通信學院，重慶 400035）

0 引言

20世紀90年代初，隨著移動通信的發展，陣列信號處理技術被引入移動通信領域，形成了智能天線這一新的研究領域［1］。它結合了自適應天線技術的優點，通過特定準則下的自適應算法，調整各天線陣元的權值、形成波束動態跟蹤期望用戶、在干擾方向上產生零陷，從而實現智能接收［2］。其核心是智能天線實現的算法，而LMS算法和遞推最小二乘（RLS，Recursive Least Square）算法則是自適應濾波兩類最基本的算法。LMS算法因其結構簡單，穩定性好，一直是自適應濾波算法中經典、有效的算法之一，被廣泛應用于自適應控制、雷達、系統辨識及信號處理等領域［3］。但是，固定步長LMS算法在收斂速度與穩態失調之間存在相互矛盾。步長越小，穩態時的失調量就越小，但算法的收斂速度慢；步長越大，收斂速度快，但失調量和穩態誤差增大。為解決這一矛盾，人們提出了多種變步長LMS算法，現所給算法也是基于變步長的一種新的LMS自適應算法。

1 LMS算法簡介

LMS算法是由Widow和Hoff于20世紀60年代初提出的［4］。其基本思想是通過調整濾波器的自身參數，使濾波器的輸出信號與期望響應之間的均方誤差最小。

自適應線性濾波器的原理框圖如圖 1所示［4］。X(n)為天線陣列接收到的信號，是一個時間序列，其元素由一個信號在不同時刻的取樣值構成；W(n)為自適應濾波器的加權矢量，由自適應線性濾波器的M個權系數構成；輸出響應表示為y(n)，d(n)為參考信號，參考信號與輸出響應之差稱為誤差信號，用e(n)表示。其中：M為濾波器的階數；

圖1 自適應線性濾波原理框

自適應線性濾波器按照誤差信號均方值(或平均功率)最小的準則，即：

來自動調整權矢量,E[e2(n)]為自適應濾波器的性能函數，記為ξ。

基本LMS算法的迭代公式為：

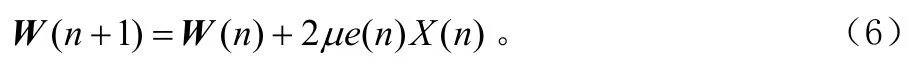
μ為步長因子，決定自適應算法的收斂速度，權向量均值收斂時，μ必須滿足：

λmax是輸入信號自相關矩陣R的最大特征值。在實際應用中，自相關矩陣的最大特征值λmax通常是未知的，因此，采用LMS算法的均方收斂條件，即μ滿足不等式［5］

式中，tr[R]是自相關矩陣R的跡。根據矩陣代數知［4］：

由式(8)和式(9)，得：

雖然μ取常數時算法簡單，易于實現，但其收斂速度慢，穩態失調系數大。

2 一種新的變步長LMS算法

對步長因子的各種改進算法雖然原理不同，但都遵循同樣的調整原則，即在初始收斂階段或系統參數發生變化時選取較大步長，以便有較快的收斂速度實現對時變系統的跟蹤；而在算法收斂后，系統獲得的權值矢量已經接近最優權值矢量，需要選取較小的步長，用以減小穩態誤差［6］。

現在滿足上述步長調整原則的基礎上，根據文獻［6］和文獻［7］的思想，提出一種新的變步長LMS自適應算法。對雙曲正割函數做簡單函數變換，令y=1-sech(x)，其中sech(x)=2/(ex+e?x)。由于該函數可作無窮階微分，所以曲線足夠平滑，同時，自變量變化很小時，函數值也變化很小。其圖形為圖2所示。

由圖2看出，y所表示的函數是一條過原點的光滑曲線，且在初始階段y隨x的變化緩慢；當x接近0時，由于函數底部平滑，y隨x的變化依舊緩慢。文獻［6］和文獻［7］采用的數學函數均存在自變量與函數值呈線性變化的現象，使穩態誤差變大。將x換成e(n)，y換成μ(n)，e(n)是μ(n)的函數，即得新的步長因子 μ(n)=β{1-sech[αe(n)γ]}，0＜μ(n)＜1/λmax。參數β控制步長曲線的取值范圍,影響算法的收斂速度,α、γ控制步長曲線在誤差接近零時的形狀［6］。新算法的迭代公式如下所示：

圖2 y=1?sech(x)

圖3為α、γ分別取1，β取0.006、0.007、0.008時，μ(n)隨e(n)的變化曲線，圖3的縱坐標是在10-3數量級上，可以看出μ(n)隨β的增大而增大，即增大β可以加快算法的收斂速度，但為了防止發散，β不易過大。圖4為γ取1，β取0.007，α取1、2、3時，μ(n)隨e(n)的變化曲線。可以發現，μ(n)隨α正比增長，但α越大，在誤差接近0時，步長的變化就越劇烈，不利于減小穩態誤差。圖5是α取1，β取0.007，γ取1、2、3時μ(n)隨e(n)的變化曲線。如圖所示，γ增大，收斂速度加快，在誤差接近0時，步長減小且趨于平緩，可以有效減小穩態誤差。但經反復實驗，γ增大，穩態誤差的穩定性降低，算法的計算量增大，所以γ一般取1。圖4、圖5的縱坐標都是在10-3數量級上。

圖3 α、γ固定，β變化時的步長曲線

圖4 β、γ固定，α變化時的步長曲線

圖5 α、β固定，γ變化時的步長曲線

3 仿真分析

現采用 MATLAB仿真工具對所提算法進行仿真驗證。輸入單頻信號s=sin(0.5πt)，噪聲為0均值的高斯白噪聲，信噪比為3 dB，輸入信號的抽樣點數為1 024，濾波器階數為128，統計訪真次數為100次。圖6為α取2，β取0.007，γ取1、2、3時算法的收斂曲線。由圖可以看出，γ取2、3時，收斂速度加快了，但穩態誤差的穩定性不如取1時好。圖7為α取2，γ取1，β取0.006、0.007、0.008時算法的收斂曲線。如圖所示，β取0.008時算法的收斂速度最快。圖8為β取0.008，γ取1，α取1、2、3時算法的收斂曲線。可以看出，α取2和3時收斂速度沒有顯著變化，取3時略優于取2時。

圖6 α、β固定，γ變化時的收斂曲線

經大量實驗得出，α，β，γ分別 取3，0.008，1時算法的權值達到最優。圖 9即為這里所提變步長因子μ(n)=β{1-sech[αe(n)γ]}，在α取3，β取0.008，γ取1時與固定步長因子μ=0.001時的收斂曲線。由圖 9可以看出，這里所提出的變步長LMS自適應濾波算法在收斂速度上遠遠快于固定步長LMS算法，且收斂后穩態誤差失調量較小。

圖8 β、γ固定，α變化時的收斂曲線

圖9 這里算法與基本LMS算法的比較

4 與其他變步長LMS自適應算法的比較

文獻［6］根據步長因子的調整原則，構造過零點、單調平滑的函數作為算法的變步長因子。將雙曲正切函數的自變量加絕對值，得到變步長因子文獻［7］分析了現有幾種 LMS自適應算法存在的缺點，利用反正切函數提出一種新的算法，使步長和誤差之間具有更好的非線性函數關系，其變步長因子為圖 10為這里算法與上述兩種算法在參數因子均取最優值時μ(n)隨e(n)變化的函數曲線。

圖10 三種算法的步長曲線

如圖所示，新算法的函數收斂速度快，誤差穩定性好。文獻[6]中的函數雖然收斂速度快，但是誤差的穩定性差，文獻[7]中的算法穩態誤差性能較好但收斂速度慢。圖11為三種算法的收斂曲線，進一步說明現所提 LMS自適應算法在收斂速度和穩態誤差上均優于文獻[6]和文獻[7]中的LMS算法。

5 結語

根據變步長LMS算法的步長調整原則提出一種新的變步長LMS自適應算法。通過控制步長因子，在加速收斂的同時，使穩態誤差趨于平緩，有效控制了穩態誤差的失調量。這里還對參數的選擇進行了詳細分析，在α取3，β取0.008，γ取1時算法權值接近最優。通過與其他算法的比較，進一步說明了該算法的有效性，為智能天線算法的研究提供了新的思路。

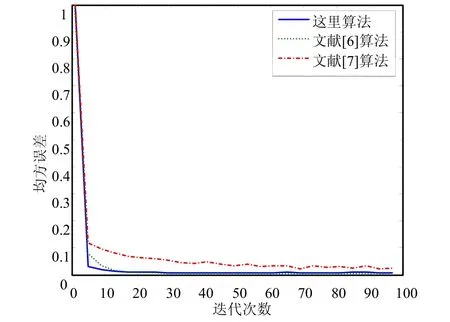
圖11 三種算法的收斂曲線

[1] CONSTANTINE A B.Antenna Theory:Analysis and Design[M].USA:Wiley Interscience,2005.

[2] 李佳靖,金榮洪,耿軍平.CDMA系統中一種快速有效的盲波束形成算法[J].西安電子科技大學學報,2007,34(06):980-985.

[3] 聶聰,呂振肅.一種新的變步長NLMS自適應算法[J].通信技術,2007,40(12):87-89.

[4] 張賢達.現代信號處理[M].北京:清華大學出版社,2002:188-192.

[5] WIDROW B,STEARNS S D.Adaptive signal processing[M].[s.l.]:Prentice-Hall,1985.

[6] 鐘慧湘,鄭莎莎,馮月萍.基于雙曲正切函數的智能天線變步長LMS算法[J].吉林大學學報,2008，46(05):935-939.

[7] 朱斌,馬艷.一種新的變步長LMS算法分析[J].計算機仿真,2008,25(09):93-95.