一種類正交矩陣產生方法

單俠芹，潘 洋，殷奎喜，趙 華

（南京師范大學 物理科學與技術學院，江蘇 南京 210046）

0 引言

CDMA在CDMA通信系統中，它的用戶編碼采用的是一個PN偽隨機序列，常用的偽隨機碼有m序列碼、gold碼、截斷碼等。但一般偽隨機（PN）序列采用的本原多項式通常最高次數為42，本原多項式有限，限制了用戶數量[1]。

CDMA系統采用walsh矩陣作為它的信道編碼。walsh矩陣的每一行（或列）都是正交碼組[2]。

m序列、gold序列和walsh序列是目前CDMA系統中廣泛采用的擴頻序列[3]。m序列和gold序列具有正交性差、可用碼組少的特點；walsh序列是由哈達碼矩陣（H矩陣）擴展而來，所以walsh矩陣大小只能是2的指數次方，不可能是任意值，且由于H矩陣的大小有限（n≤200內除去n=188），所以以上三種擴頻序列都限制了 CDMA系統的用戶數目。所以可以用類正交矩陣代替他們應用到CDMA、多載波碼分多址（MC-CDMA）和測距等系統中。

1 窮舉法

窮舉法也叫枚舉法或列舉法[2]。在研究對象是由有限個元素構成的集合時，把所有對象一一列舉出來，再對其一一進行試驗，找出符合條件的解的方法。這里所研究的對象（元素）可以是各個個體事物，也可以是構成研究對象的各類事物，在這里所研究的對象是類正交矩陣。

對于許多毫無規律的問題而言，窮舉法用時間上的犧牲換來了解的全面性保證，尤其是隨著計算機運算速度的飛速發展，窮舉法的形象已經不再是最低等和原始的無奈之舉，比如經常有黑客在幾乎沒有任何已知信息的情況下利用窮舉法來破譯密碼，足見這種方法還是有其適用的領域的。

2 類正交矩陣

在一個矩陣中，設各個碼組長度為n，每個碼元只取+1和-1，x和y是該矩陣中的兩個碼組：

其中，xi,yi∈(+1,?1),i=1,2,…,n，則x和y間的互相關系數[4]定義為：

若碼組x和y完全正交，則必有ρ(x, y)=0，說明碼組間不相關；若x和y不完全正交，則ρ(x, y)≠ 0，說明x和y之間具有一定的相關性，稱x和y為類正交；若碼組x和y完全相同，則ρ(x, y)=1，說明碼組具有很好的自相關特性[5]。由此可見，若碼組x和y的相關系數ρ(x, y)越小，說明它們的互相關性越弱；若碼組x和y的相關系數ρ(x, y)越大，說明它們的相關性越強[6]。

由r個“0”和“1”組成的碼組共有2r種可能，因為全“0”和只有一個“1”的碼組所含的信息量太少，除去全“0”行和只包含一個“1”的可能，剩下2r?r?1種可能，由這2r?r?1種可能組成一個矩陣，即原始矩陣w，但是該矩陣的每行之間并不一定正交或是滿足相關值ρ∈ (?1，1)，部分序列的相關性如圖1所示。

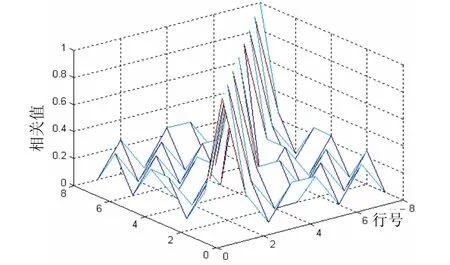
圖1 部分篩選后的類正交矩陣的相關系數

由圖1可以看出，有一部分行向量之間的互相關系數值比較大，這說明在矩陣中存在一部分互相關性較差的行向量。在實際使用中，利用類正交矩陣的類正交特性，可以將矩陣中的行向量作為用戶編碼或信道編碼應用于 CDMA等通信系統[7]，如果作為編碼的行向量之間的互相關性較強，則會嚴重影響解碼后恢復出的各路用戶信號的效果。所以需要將原始矩陣w經過根據窮舉法設計的算法進行篩選，從而篩選出互相關系數較小，即正交性較好的行向量作為多址通信中的用戶編碼。但是，經過篩選之后，雖然得到了具有更好正交性的矩陣，但是由于剔除了一些互相關系數大的行向量，所以由篩選后的向量組成的矩陣的大小將會變小，也就是可用于編碼的序列的數量變少了，這也限制了可接入系統的用戶的數量。

3 類正交矩陣的產生

這里介紹一種運用窮舉法得到滿足條件的正交或類正交矩陣的算法。首先，根據第2部分的描述產生原始矩陣，具體步驟如下：

①產生2r所有可能的碼組，將其保存到矩陣w中，即得到r×r的矩陣；

②篩選：刪除全“0”和只有一個“1”的碼組；

③數值轉換：用 “-1”代替原碼組中二進制數字“0”，用“+1”代替原碼組中的二進制數字“1”，這樣得到原始矩陣w。

其次，運用窮舉法設計算法，從原始矩陣中找到滿足要求的正交或類正交矩陣，框圖如圖2所示。

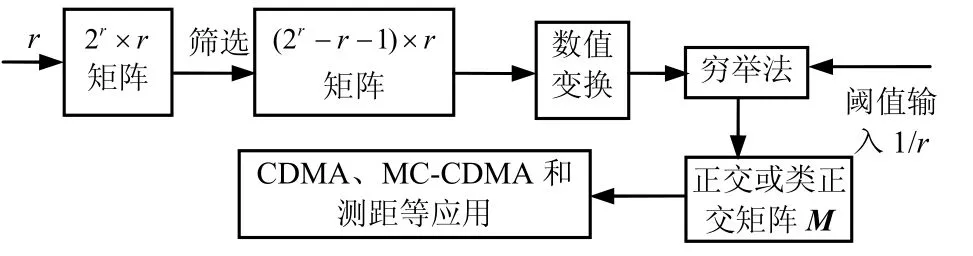
圖2 正交或類正交矩陣的產生框

其中應用窮舉法進行篩選的算法描述如下：采用最大似然準則判決法，將閾值（即相關值）設置為 0，即σ=0，則得到的矩陣即為完全正交陣，若將閾值設置為某個非常接近0的值（?1＜σ ＜1），則可得到相應的類正交陣。這里假設σ=0，得到的矩陣都為完全正交的矩陣，若想得到類正交陣，只需改變閾值即可。

具體步驟如下所述：

①以原矩陣w的第一行為例，按照式（1）計算第2～n行與該行的互相關系數ρ，記錄下ρ=0的行，并將其行號保存到矩陣w1中；

②以w1矩陣的第一個元素所記錄的行號為原矩陣的第一行，重復步驟①搜索與該行相關系數不滿足給定值的行，并從w1矩陣中刪除該行，此時i的范圍為[1,m?1]；

③根據步驟②得到的新矩陣 w1，重復步驟②，直到m＜2；

④以w1矩陣中的第i個元素值為原矩陣的第一行，重復步驟②～③可以得到新的一組正交矩陣M；

⑤重復步驟①～④，得到不包含第 i（i∈[1,n-1]）行之前所有行的正交矩陣。

其中n=2r-r-1，m為計算所得的w1矩陣大小。

根據上面算法得到的矩陣中任意碼組之間的相關系數都為0，即碼組之間是兩兩正交。現把這種兩兩正交的碼組所組成的矩陣稱為正交矩陣。若改變閾值σ的大小，使相關系數在(0,1)之間，則得到的矩陣為類正交矩陣。下面分別為不同閾值和r大小不同時得到的部分正交陣M和類正較陣M。

設r=7，閾值為1/r時，通過窮舉法得到的部分類正交矩陣如表1所示，表中的數據都是十六進制，每一行都是一個類正交矩陣M。

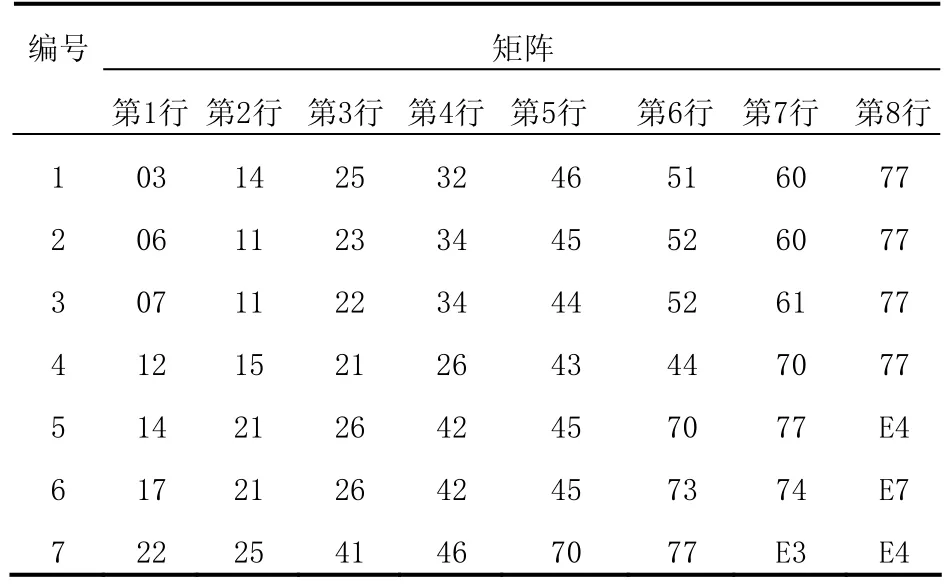
表1 r=7時的部分類正交矩陣

其中第一行所表示的二進制類正交矩陣如表2所示。

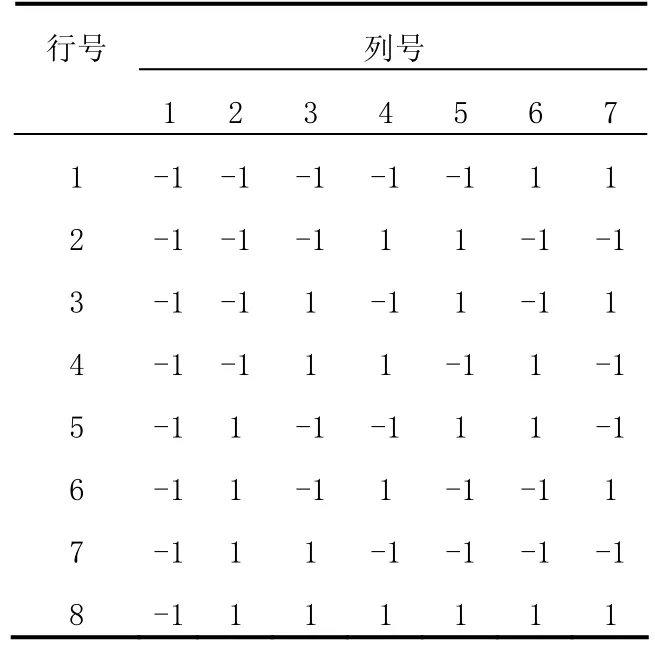
表2 表1中第一行所表示類正交矩陣M

設r=7，閾值為0時，通過窮舉法得到的部分完全正交矩陣如表2所示，同表1、表3中的數據也都是十六進制，每一行都是一個正交矩陣M。

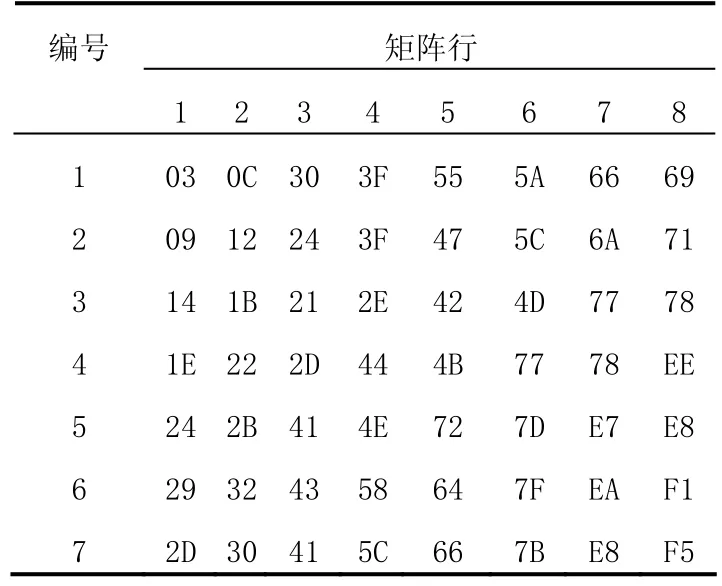
表3 r=8時閾值為0得到的部分正交陣

表1和表3只是篩選出的部分類正交矩陣和部分正交矩陣，拒不完全統計，當r=8，閾值為1/r時，能夠得到的符合條件的類正交矩陣數量n?100，矩陣大小最大為8×7。

對于傳統的walsh矩陣而言，其行向量或者列向量的個數總是2的指數次方[8]，不可能出現非2的指數次方的矩陣。表1產生的類正交矩陣，與Walsh矩陣類似的正交性，具有良好的自相關和互相特性，但是它們的矩陣的大小和數量由互相關系數的大小和碼長確定，不再受到2的指數次方的限制；同樣碼長的矩陣比WALSH矩陣有更多碼組，具有相似相關性的矩陣數量隨著碼長和互相關系數的不同而不同，碼長越長、互相關系數越大長符合條件的類正交矩陣越多，可以隨機選擇其中的任意一個作為 CDMA的用戶編碼，增加擴頻序列的不確定性。

4 結語

提出一種用窮舉法產生類正交矩陣的方法，并對該方法進行了闡述和分析。并比較了它和WALSH矩陣的區別，與WALSH矩陣相比有了很大的改進，所以很多應用 WALSH矩陣的地方都可以用類正交矩陣來代替。另外，如果要求篩選出的矩陣之間完全正交，即在下一步篩選之前從原矩陣中剔除已篩選出的矩陣，這樣篩選出的矩陣可以應用到各個不同的小區或不同的“物體”上，保證了小區之間不受影響，如物聯網、蜂窩網等。

[1] 王玉德，王金新.基于MATLAB的調頻擴頻通信系統的仿真研究[J].通信技術，2010，43（06）：21-23.

[2] 王曉東.計算機算法設計與分析[M].北京：電子工業出版社，2005：86-113.

[3] 張治元，蔣清泉，宋燕輝.TD-SCDMA系統擾碼規劃算法及仿真[J].通信技術，2010，43（06）：176-178.

[4] 樊昌信，曹麗娜.通信原理[M].北京：國防工業出版社，2007.

[5] WELCH L R.Lower Bounds on the Maximum Cross Correlation of signals[J].IEEE Transactions on Inform, Theory, 1974, 20(05):397-399.

[6] 査艷芳.多維類正交偽隨機矩陣及其擴展[D].南京：南京師范大學，2010.

[7] Roy Blake.現代通信系統[M].北京：電子工業出版社，2003.

[8] WILIANMSON J.Hadamard’s Determinant Theorem and the Sum of Four Squares[J].Duke Mathematical, 1944(11):65-81.