夾層結構模型假設對振動和聲傳輸特性影響研究

王 晴 洪 明 周艷秋

1中國艦船研究設計中心，湖北 武漢 430064

2大連理工大學工業裝備結構分析國家重點實驗室運載工程與力學學部船舶工程學院，遼寧大連 116024

3中國艦船研究設計中心，上海 201108

夾層結構模型假設對振動和聲傳輸特性影響研究

王 晴1洪 明2周艷秋3

1中國艦船研究設計中心，湖北 武漢 430064

2大連理工大學工業裝備結構分析國家重點實驗室運載工程與力學學部船舶工程學院，遼寧大連 116024

3中國艦船研究設計中心，上海 201108

不同模型假定下夾層結構的聲振特性各不相同。基于Reissner模型和Zig－Zag模型位移場假設，分別建立了兩種復合材料夾層板有限元動力單元模型，并通過推導的模型編制了計算程序，采用子空間迭代法求得了其固有頻率和固有振型，采用混響聲場聲傳輸理論計算了傳聲損失，并對夾層板的動力特性和聲傳輸特性進行了數值模擬研究，同時還考慮了夾層結構面板與芯板的厚度比和彈性模量比不同時各種模型的適用范圍。

Reissner模型；Zig－Zag模型；Mindlin理論；振動特性；傳聲損失

1 引言

隨著各個工程領域對材料要求的不斷提高，復合材料夾層板也得到了廣泛的應用。尤其是在船舶設計中，開始越來越多地應用夾層結構。通常，設計者們均十分關注船舶的居住性和舒適性，而這又與其結構振動狀況和隔聲狀況密切相關，因此，對夾層結構的振動特性和聲傳輸特性研究具有實際意義。

對于夾層板問題的研究，大多是以上世紀40～50年 代 建 立 起 來 的 Reissner、Hoff和∏pycakob 理論為基礎［1－3］，這 3 種理論對求解均勻材料面板的夾層結構比較有效。

1）Reissner理論

該理論認為面板很薄，假設其主要承受面內應力為 σx、σy和 τxy，且都沿板厚度均勻分布。 在芯層內，σx＝σy＝τxy＝0， 芯層可抵抗橫向剪切力，并考慮了芯層橫向剪切變形的影響。當夾層板關于中面做反對稱彎曲變形時，假設面板和芯層內都有εz＝0。在面板和芯層內，都不計σz對形變的影響。

該理論把面板作為只承受面力的薄膜處理，忽略了本身的抗彎剛度，而夾芯則假設其僅具有抗橫向剪切能力，這是一種最簡單的夾層板理論。

2） Hoff理論

該理論認為表層面板很薄，只把它們看成是通常的彈性薄板。 在芯層內，σx＝σy＝τxy＝0，考慮了芯層橫向剪切變形的影響。當夾層板對中面作反對稱變形時，假定芯層εz＝0，忽略了σz對形變的影響。

該理論將面板視為普通薄板，即只考慮了其面內應力和抗彎剛度，而對于夾芯部分，則仍認為其僅具有抗橫向剪切能力。該理論和Reissner理論都沒有考慮夾芯的其他變形能力。

夾層板在轉動時，面板和芯層的轉角是不一致的，其位移具有齒形特征，尤其是當厚度較大或材料較軟時，忽略轉動項將會帶來較大誤差［4］。本文推導了忽略面板轉動項的Reissner理論有限單元模型和考慮面板轉動項的基于Hoff理論基礎上Srinivas提出的Zig－Zag模型。計算了夾層板的面板和芯板厚度比逐漸增加和彈性模量比逐漸增加時，結構自由振動固有頻率和混響聲場入射情況下夾層板傳聲損失的變化情況。

2 夾層板自由振動有限元分析理論

2.1 模型示意圖、自由度及位移場假設

夾層板由上下面板和中間芯層組成。以夾層板中性面為坐標平面，建立整體坐標系，其形式如圖1所示。

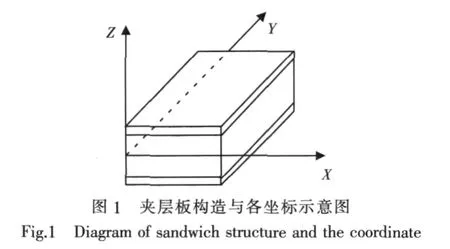
基于Reissner模型假定和Mindlin一階剪切理論，單元每個節點有5個自由度，即沿3個方向的位移 u0、ν0、w0，以及繞 2 個軸的轉角 θx和 θy，夾層板單元的位移場假設為：

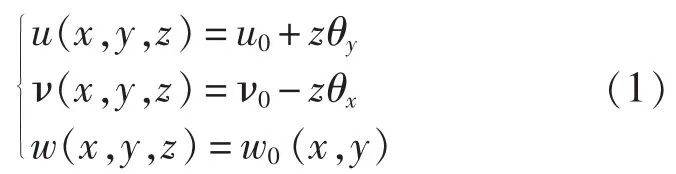
基于Hoff理論基礎上的Zig－Zag模型假定和Mindlin一階剪切理論，單元每個節點有9個自由度：即芯板的 5 個自由度 u0、ν0、w0、θx和 θy，以及上下面板各兩個自由度 φx、φy和 φx、φy， 夾層板單元各層的位移場假設為：

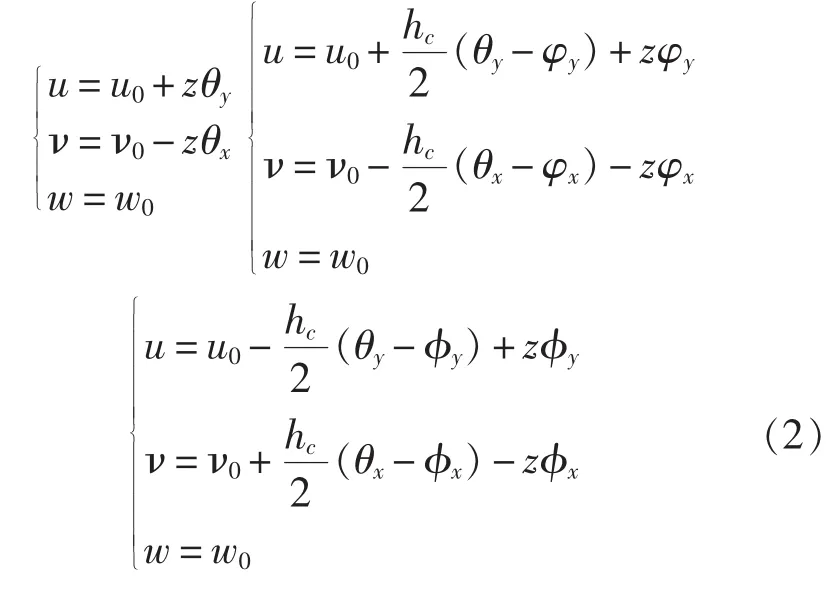
2.2 兩種模型夾層板結構振動有限元推導

對于夾層板自由振動有限元理論，其與普通板的區別在于，由于各層的材料參數和幾何參數不同，其質量陣和剛度陣需進行疊加。

4節點夾層板的剛度陣和質量陣的形成步驟為：按照位移插值函數和材料本構關系，可得到形函數矩陣［N］、密度矩陣［ρ］和幾何矩陣［B］。

對于Reissner模型，其彈性矩陣可將芯板彈性 陣［Dc］、上面板彈性陣［Du］和下面板彈性陣［Dd］進行疊加，從而得到夾層板總的彈性矩陣［5］：

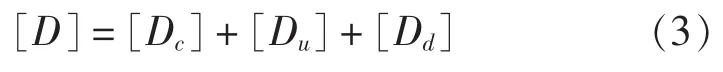
進而，能夠得到夾層板總的剛度矩陣：

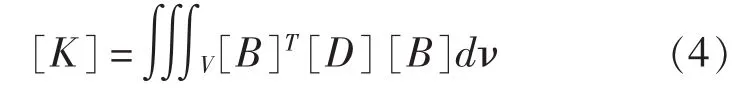
對于Zig－Zag模型，上下面板的幾何矩陣［B］也不相同，需要每一層形成各自的剛度矩陣之后再進行疊加［6］。

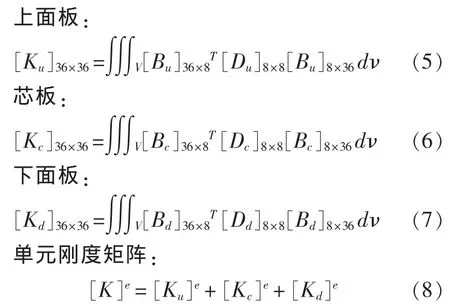
質量陣的形成方法與剛度陣相同。

設在結構上作用有激勵｛f（t）｝，結構產生的響應為｛x（t）｝，由 Hamilton 原理，在動載荷作用下，結構的振動方程可以表示為：

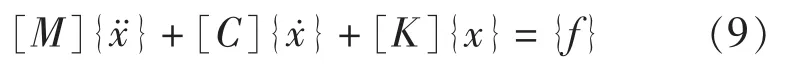
式中，［M］、［C］、［K］分別為結構的質量矩陣、阻尼矩陣和剛度矩陣。求解對應的齊次方程，可得到該結構相應的固有頻率 ωj和振型｛φ｝j。

2.3 兩種模型夾層板結構傳聲損失模型

選取混響聲場模型為比較理想的單頻模型，其假設為，是在各個方向上聲壓的幅值和相位隨機。這是一種很接近真實的混響聲場的模型，具體表示為［7－8］：

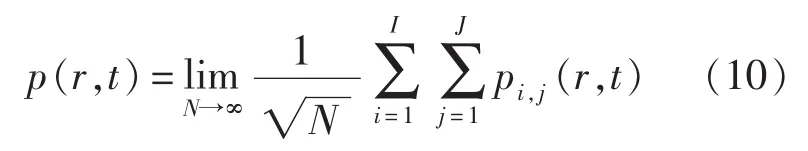
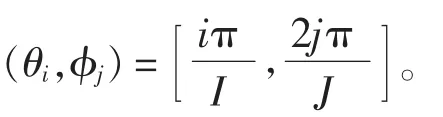
因此，混響聲場的入射聲功率可以認為是I×J列平面聲波的入射聲功率相疊加。若空氣中板的長和寬分別為a和b，以角度（θ，φ）入射的平面聲波的入射聲功率∏i為：

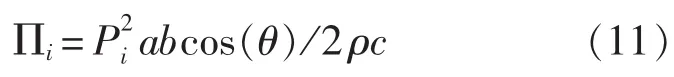
式中，ρ為輻射介質的密度；c為聲音在介質中的傳播速度。

夾層板在平面聲波作用下的傳聲損失TL可以定義為：

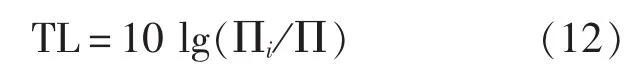
式中，∏為結構在平面聲波激勵下的輻射聲功率。

計算結構輻射聲功率的方法很多，本文采用的是基于結構表面振速計算輻射聲功率。

式中，Re（）表示取實部；νn*（P）表示表面 νn（P）的共軛復數。

3 數值模擬

下面，將選取典型算例來驗證模型的適用性問題。四邊剛固夾層板長2 m、寬1.5 m，芯層材料參數 E2＝ 8.96 × 108Pa， μ2＝ 0.42， ρ2＝ 999 kg／m3，厚1 cm。上下表層為厚度相等的鋼板，分別為1 mm、3 mm、6 mm 和 9 mm，E1＝2.1×1011Pa，μ1＝0.3， ρ1＝7 800 kg／m3，夾層板分析網格為8×6 個，單元劃分和節點編號模型如圖2所示。

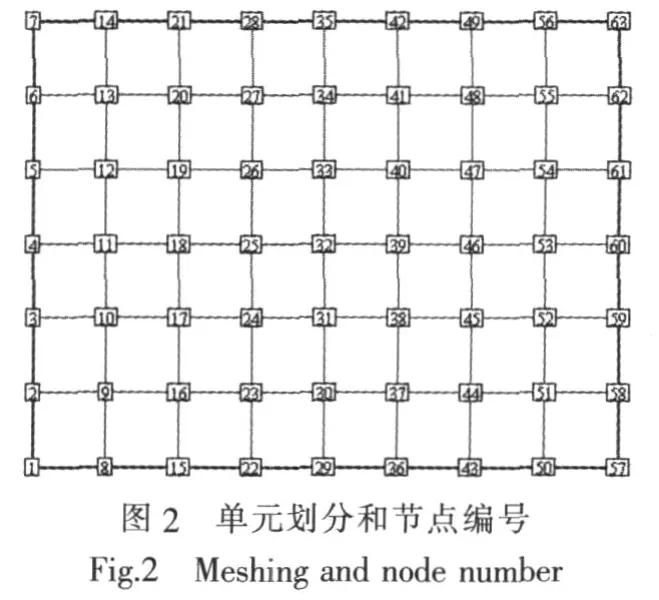
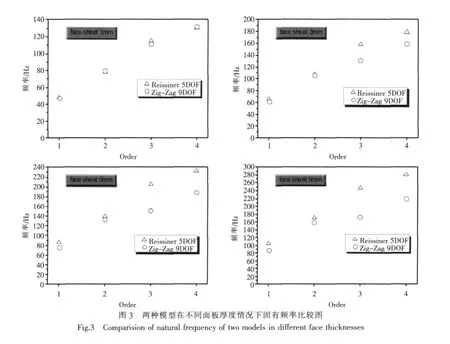
上下面板厚度為1 mm、3 mm、6 mm和9 mm的夾層板前四階固有頻率對比如圖3所示。

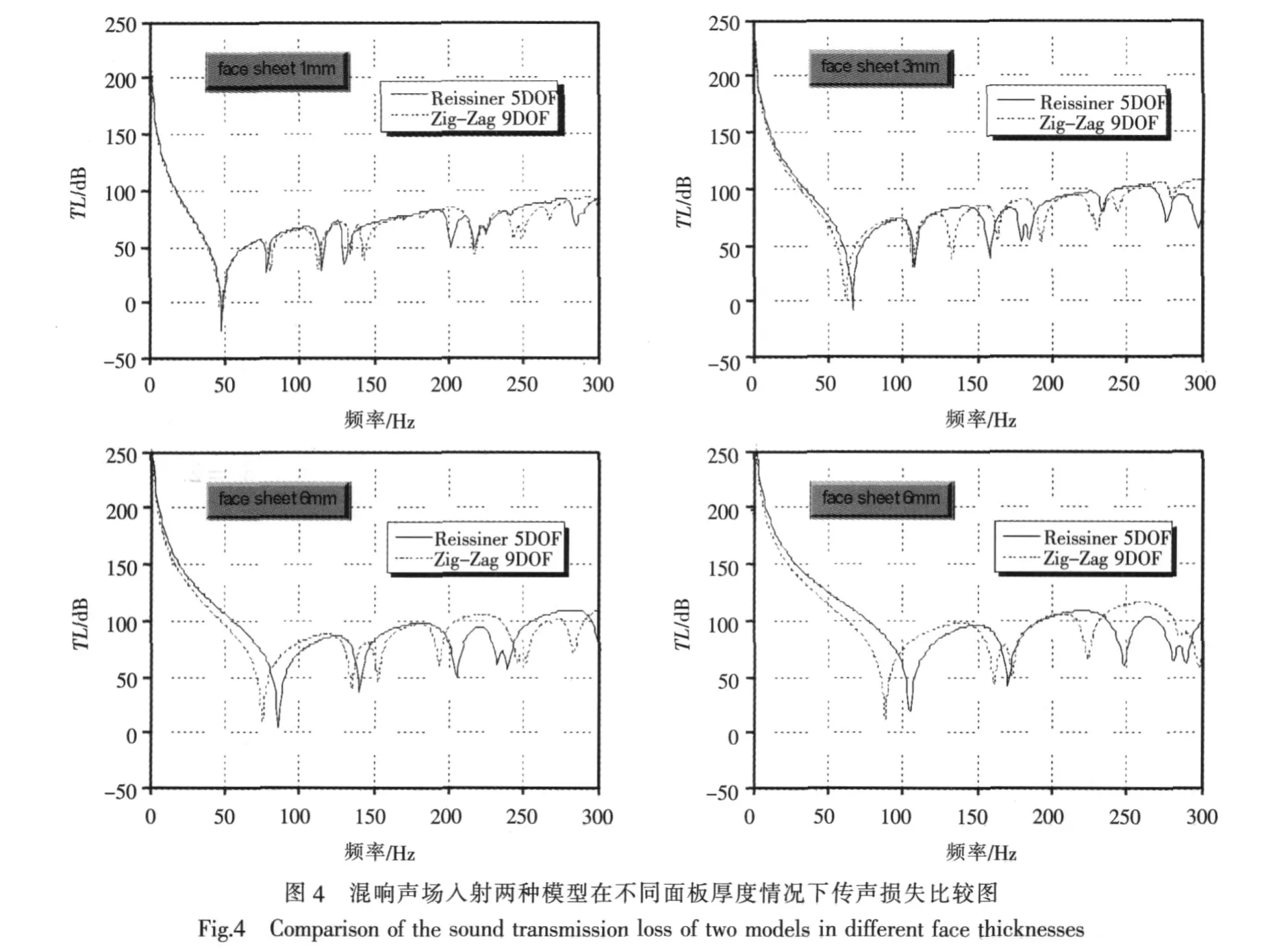
在混響聲場激勵下，夾層板的傳聲損失對比如圖4所示。

若夾層板邊界條件和板的長寬不變，芯層彈性 模 量 分 別 取 E2＝8.96 ×106Pa、8.96 ×107Pa、8.96 ×108Pa 和 8.96 ×109Pa， μ2＝0.42， ρ2＝ 999 kg／m3， 厚度為 1 cm。 上下表層為鋼板，E1＝ 2.1 ×1011Pa， μ1＝ 0.3， ρ1＝7 800 kg／m3， 厚度相等，分別為1 mm。單元劃分和節點編號不變。

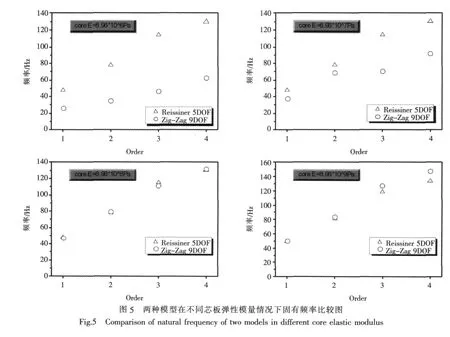
芯板的彈性模量為 8.96 ×106Pa，8.96 ×107Pa，8.96×108Pa和 8.96×109Pa的夾層板前 4 階固有頻率對比如圖5所示。

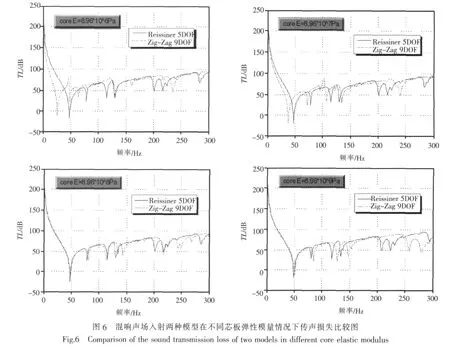
在混響聲場激勵下，夾層板的傳聲損失對比如圖6所示。

4 結論

經過對2種模型的計算分析，得出以下結論：

1）在2種模型夾層板面板厚度逐漸增加的情況下，結構振動的固有頻率在面板厚度不足芯板厚度的1／10時幾乎相同。隨著厚度的增加，2種模型所得結果的差距會逐漸增大。在混響聲場入射情況下，夾層板的傳聲損失整體保持不變，但傳聲損失低谷產生的位置由于固有頻率不同，也有差別。

2）在2種模型夾層板芯板彈性模量逐漸增加的情況下，結構振動的固有頻率在芯板的彈性模量不足面板的0.4%時相差很大。隨著芯板彈性模量的增加，2種模型所得到的結果趨于相等。在混響聲場入射情況下，夾層板的傳聲損失整體保持不變，但傳聲損失低谷產生的位置由于固有頻率不同，也有差別。

3）模型化的差異對結構振動的固有頻率影響很大。在工程計算中，當面板厚度與芯板厚度相比較大或面板剛度與芯板剛度相比較大時，Reissner理論已不能滿足計算精度的要求，而應選擇一些精度更高的單元。但在面板厚度較小或彈性模量相差不大時，Reissner理論的計算方法由于節省計算空間，也具有其自身的優越性。

［1］白瑞祥，陳浩然，蘇長健.考慮面板和芯體剪切效應的復合材料夾層板穩定性的有限元分析［J］.玻璃鋼／復合材料，1999（5）：3－6.

［2］師俊平，劉協會，越居才，等.復合材料夾層板的振動及阻尼分析［J］.應用力學學報，1996，13（2）：132－136.

［3］BANERJEE J R，SOBEY A J.Dynamic stiffness formulation and free vibration analysis of a three－layered sandwich beam ［J］.International Journal of Solid and Structures，2005，42（8）：2181－2197.

［4］CHO Y B，AVERILL R C.First－order zig－zag sublaminate plate theory and finite element model for laminated composite and sandwich panels［J］.Composite Structure，2000，50（1）：1－15.

［5］周艷秋.艦船基層結構動力響應特性分析［D］.大連：大連理工大學，2005.

［6］白瑞祥，張志峰，陳浩然.基于Zig－Zag變形假定的復合材料夾層板的自由振動 ［J］.力學季刊，2004，25（12）：528－534.

［7］RAFAELY B： Spatial－temporal correlation of a diffuse sound field ［J］.Journal Acoustical Society of America，2000，107（6）：3254－3258.

［8］JACOBSEN F，ROISIN T.The coherence of reverberant sound field ［J］.Journal Acoustical Society of America，2000，108（1）：204－210.

Effects of Model Assumption on the Characteristics of Vibration and Sound Transmission in Sandwich Structure

Wang Qing1Hong Ming2Zhou Yan－qiu3
1 China Ship Development and Design Center， Wuhan 430064，China
2 School of Naval Architecture Engineering， Faculty of Vehicle Engineering and Mechanics，State Key Laboratory of Structural Analysis for Industrial Equipment， Dalian University of Technology， Dalian 116024，China
3 China Ship Development and Design Center，Shanghai Division，Shanghai 201108，China

With variable assumed sandwich model， the vibration and acoustic characteristics are distinct.Based on the displacement field assumption of the Reissner and Zig－Zag model， the paper established two kinds of composite sandwich plate Finite Element models， and its inherent frequency and Eigen－mode shapes were required by subspace iteration method with the help of the derivation model program.The paper also calculated the acoustic transmission loss by transmission theory of diffused sound field，and studied the numerical simulation of vibration and sound transmission character，the application of sandwich plate＇s face and core with variable thickness ratio and elastic modulus ratio were considered as well.

Reissner model； Zig－Zag model； Mindlin method； vibration character； sound transmission loss

TB532

A

1673－3185（2011）03－68－05

10.3969/j.issn.1673-3185.2011.03.015

2010-03-18

國家自然科學基金資助項目（51079027）

王 晴（1984－），女，碩士。研究方向：復合材料結構動力學。E-mail：sunnywangqing＠126.com

洪 明（1959－ ） ，男，教授。 研究方向：結構失效、振動和噪聲機理、預極及控制研究。E-mail：mhong＠dlut.edu.cn