干燥路面上輪胎制動距離的FEM仿真

臧孟炎,陸 波,陳玉祥

(華南理工大學機械與汽車工程學院,廣州 510640)

前言

汽車的制動性能是有效減輕或避免交通事故的一個重要因素。隨著交通法規越來越嚴格,要求各個汽車生產廠家必須公布每款產品從 100km/h開始制動到完全靜止時所行駛的距離,但到目前為止,汽車的制動距離通常只能通過試驗得到。為了既滿足交通法規要求又縮短產品開發周期,在產品設計階段,通過數值仿真方法對汽車的制動距離進行有效預測非常重要。

眾所周知,輪胎是汽車與路面的唯一接觸部位,汽車制動基本上依靠輪胎實現(風阻有一定貢獻)。所以,在某種意義上,可以認為輪胎的制動性能決定汽車的制動性能,特別是主機廠選配輪胎進行制動性能評價時尤為如此,因為此時除輪胎不同外,其他部分完全一樣,汽車制動性能的優劣取決于輪胎的制動性能。

然而,在有限元仿真分析方法廣泛應用于汽車及主要零部件各種性能評價的今天,對輪胎制動性能的分析和評價,目前仍然主要依賴試驗。究其原因,主要是輪胎制動過程伴隨著大變形和沖擊,隱式有限元方法難以應對而只能寄希望于顯式有限元方法。但是,汽車的制動過程特別是濕滑路面的制動時間長達數秒,冗長計算時間和數據累計誤差使顯式有限元方法難以實現完全模擬,而且沒有實際工程意義。為此,文獻[1]和文獻[2]中提出了根本解決上述問題的離散化方法:將制動過程按速度離散化,通過顯式有限元分析各離散速度下的制動器摩擦熱損失率和輪胎與路面的摩擦能量損失率,再近似求得制動時間和制動距離。

本文中在介紹制動過程離散化仿真分析方法的基礎上,具體分析光面輪胎在干燥路面的制動時間和制動距離,以確認其計算效率和精度,作為花紋輪胎干濕路面制動性能仿真分析的基礎。

1 制動過程分析

圖1為常用汽車制動系統。汽車制動時,駕駛員通過制動踏板壓縮連接于制動主缸和制動輪缸軟管中的制動液,使制動器工作。可以近似認為,汽車的動能通過制動器的摩擦熱損失和輪胎與路面間摩擦能量損失而消耗,直到汽車靜止。

盡管空氣阻力和輪胎的黏彈性變形等因素也消耗汽車動能,但與上面兩個因素相比,可忽略不計。

制動時輪胎的動力學模型如圖 2所示,其中 G為1/4車質量;Fz為輪胎受到的地面反力;rs為輪胎滾動半徑;Fxb為輪胎受到的地面摩擦力,以速度v行駛的汽車制動時,制動器通過對輪轂施加制動力矩Tμ,輪轂轉動角速度 ωw下降,導致輪胎接地部分與地面產生相對滑移速度vs。輪胎滑移率為

輪胎滑移率是影響制動效果的重要因素。當車輪抱死,輪胎與地面間處于完全滑移狀態時,制動力系數明顯下降,遠遠低于滑移率為 15%時的數值,汽車容易出現跑偏或失去轉向能力。為此,目前已作為乘用車基本配置的 ABS系統根據輪胎滑移率的大小,通過控制制動輪缸壓力以調節制動摩擦面之間的結合強度,保證制動力系數在較高的水平。

2 輪胎制動過程離散化仿真

2.1 制動過程離散化

將整個制動過程按制動速度離散成多個區間,假設汽車初始制動速度為 100km/h,可將整個制動過程以速度劃分為 10個區間,區間端點速度分別為100,90,…,0km/h,參見圖 3。在每個離散速度下,建立該速度下的輪胎制動分析有限元模型,考慮ABS的作用使輪胎與路面間保持最佳滑移率(15%)來模擬制動過程,通過仿真結果求得該速度下的制動器摩擦熱損失率和輪胎與路面間摩擦能量損失率,然后使用分析方法近似求得制動時間和制動距離。這樣,“漫長”的制動過程有限元仿真分析轉化為 10個速度下簡單的制動仿真計算。

2.2 制動分析有限元模型

如圖2所示,輪胎制動時汽車前進速度為v,而車輪繞輪軸轉動的角速度為 ωw。為分析各制動速度(如50km/h)下的輪胎變形和應力狀態,須要按圖 4所示的線性加載方式給車輪轉動中心施加一個強制平移速度,同時為剛性車輪定義一個適當的、也是線性增加的轉動角速度以確保開始制動計算時輪胎滑移率為 15%。10個離散速度均采用圖4的加載方式,在 60ms內加載,20ms用于制動分析。只是在20和10km/h時,ABS失效,車輪抱死,轉動角速度為零。輪胎的充氣和汽車整質量加載過程只需進行一次有限元分析,然后將輪胎應力和位移信息作為各個加速制動過程的初始狀態即可。

2.3 制動輪缸壓力計算

用有限元法對制動距離的仿真評價很大程度上取決于所采用的制動輪缸壓力曲線pc(v)的可靠性。緊急制動時滾動阻力一般只有制動力的幾十分之一,空氣阻力也可以忽略不計,因此一般只考慮輪缸壓力、制動力矩以及地面制動力對車輪系統的作用。在 0～100km/h的速度區間內,輪胎的振動頻率遠小于滾動輪胎 1階固有頻率,所以文中不考慮輪胎的周向扭轉振動傳遞效應[3-5]。根據汽車ABS系統的控制與作用機理[6],輪胎的動態平衡關系為

式中:m為整車質量;It為單個輪胎的轉動慣量;n為輪胎個數;μs為路面與輪胎間的摩擦因數;FI為某個離散速度下輪胎接地區域節點所受地面垂直反力;N為輪胎與地面接觸區域節點個數。

聯立式(1)～式(4)方程可以得到單個輪胎制動力矩為

采用盤式制動器時制動輪缸壓力為

式中:pc為某個離散速度下制動輪缸的輸出壓力;Ac為制動軟管橫截面積;rc為制動鉗有效作用半徑;μc為制動盤上的摩擦因數。

圖5為ABS作用下制動輪缸壓力輸出曲線,通常可以把輪缸壓力大體分為A、B、C 3個區域:制動輪缸壓力經tA=0.25s的上升階段到達區域B;當汽車速度≤20km/h時,車輪被完全鎖止到達區域C。在制動過程的仿真計算時,假設汽車前后輪制動輪缸的壓力按照相同的規律變化,區域 A輪缸壓力線性上升。

利用有限元仿真軟件求得每個離散制動速度下的Fxb,多項式插值求得Fxb(v),通過式(5)～式(6)獲得pc(v)。

2.4 制動距離求解

根據能量守恒定律可得

在制動過程中輪缸壓力輸出與制動速度間存在明顯的非線性關系,把前面所分 10個速度區間 Δvi(i=1,2,…,10)再次細分成以提高仿真估計精度。在每個小區間內,減少的汽車動能等于制動器摩擦熱損失和輪胎摩擦能量損失之和(參照圖3),汽車速度從下降到的時間可以由下式得

假設A區域的滑移率為15%時,制動時間T與制動距離S分別為

式中v(t)為未修正的速度曲線。

由于區域A是制動液壓力的上升階段,而上面求得的制動時間與制動距離是假設輪胎在區域A的滑移率為 15%的條件下得到的,為了修正這兩個值,假設在這個區域路面對輪胎的摩擦力是線性增加的。由汽車動態平衡可得

因此,tA時刻的汽車速度和在區域 A的制動距離分別為

總的制動時間與制動距離可以通過下式修正:

式中:T|v=vA、S|v=vA分 別為汽車從減速到所經歷的時間與距離。

以上就是輪胎制動過程離散仿真分析的基本方法。由圖 4可知,每個離散速度下輪胎有限元制動仿真的時間只需要80ms,對于制動時間長達5s的制動問題,該方法是完整計算所需CPU時間的1/60以下。這樣,一方面可以大大減少數據累計誤差,以保證計算結果的可靠性;另一方面,使用多CPU計算機對 10個制動速度同時進行計算,保證了該仿真方法的工程應用價值,使輪胎干濕路面制動性能的仿真分析成為可能。

3 輪胎制動性能仿真分析實例

本文中使用 175/65/R14型號輪胎,為簡便起見,以不考慮花紋的光面輪胎在干燥路面的制動過程為研究對象,使用軟件Abaqus,以確認100km/h速度下制動過程離散仿真方法的有效性。

3.1 輪胎有限單元和材料模型

圖6為輪胎有限元模型截面圖。子午線輪胎中的簾布、胎冠、胎體與胎圈內嵌鋼絲簾線,使用rebar加強型單元嵌入橡膠基體單元的方法來模擬骨架材料對輪胎橡膠的增強作用。為了節約仿真計算時間,使用與胎圈外圍共節點的離散剛體單元模擬輪輞,路面使用解析剛體。

使用yeoh本構關系模型[7],以及泊松比0.495模擬橡膠材料特性,鋼絲簾線使用線彈性材料[8]。

3.2 制動模型和邊界條件

輪胎制動工況有限元模型施加邊界條件包括充氣、加載、加速和制動 4個步驟。充氣工況在2D模型中完成,然后利用Abaqus軟件中*Symmetric Model Generation與*Symmetric Results Transfer兩個關鍵字,將其轉換為 3D模型,并完成汽車整車質量的加載。這兩個工況使用隱式計算方法完成。利用*Import關鍵字將前兩個工況隱式計算結果導入,在動態顯式計算步中完成輪胎的加速與制動工況。表 1為本實例的相關參數。按圖 4所示的加載方式分別建立 10個離散速度下的輪胎制動分析模型進行制動仿真計算。

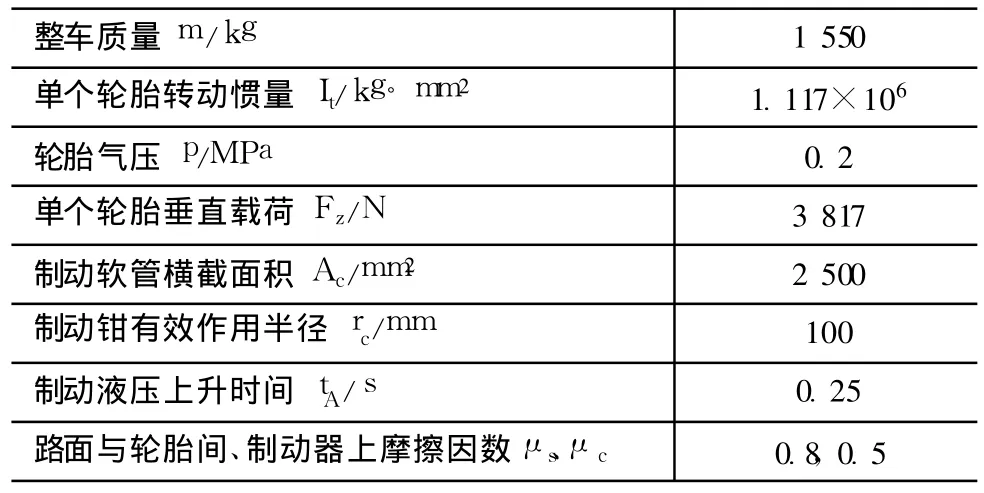
表1 制動仿真參數

4 結果分析

由于制動分析采用顯式有限元法,在每個離散速度的制動平衡階段存在如圖 7所示的振動現象,通過獲得明顯的振動周期來確定制動平衡仿真計算時間,由Abaqus軟件獲得某一離散速度下均勻分布的 20個時刻點上的輪胎接地區域節點滑移率與受到的垂直反力,利用式(2)和式(9)并取其均值,得到該離散速度制動工況下的與,同理得到其它9個離散速度下的(圖8)。在30～20km/h這個速度區間上,輪胎滑移率從 15%很快提高到100%,所以輪胎摩擦能量損失率有一個上升過程,在其他區間輪胎摩擦能量損失率均隨制動速度的降低而下降。

根據 10個離散速度下輪胎所受地面摩擦力的分布特點,對其進行3次多項式插值得到Fxb(v),如圖9所示。通過式(5)～式(6)就可得到制動力矩Tμ(v)與輪缸壓力pc(v)。

根據pc(v)與表1的相關參數,并利用式(8)就可求得(圖10),當汽車速度≤20km/h時車輪完全抱死,制動器上的摩擦熱損失為零。曲線在30km/h處有拐點,這是由于輪胎滑移率變化所致(從15%變化到100%)。

輪缸壓力上升階段tA=0.25s時,對應的制動速度為94.52km/h,由式(17)和式(18)修正后的制動時間為4.7s,制動距離為48.11m。

根據汽車制動距離計算公式[9]:

式中:τ′2為制動器間隙時間;τ″2為制動輪缸壓力上升時間;ua0為制動初速度;abmax為最大制動減速度。對應于文中所假設的仿真制動參數,τ′2=0, τ″=0.25s,ua0=100km/h,abmax=μsg=7.856m/s2,最后得到S=51.7m。式(18)與式(19)得到的計算結果接近,說明文中仿真方法可行、有效。

5 結論

建立了 175/65/R14光面輪胎制動工況有限元模型,對求解配備 ABS制動系統汽車的制動時間與距離的仿真方法做了詳細介紹。此方法能反映制動系統相關參數、輪胎的結構與材料對制動距離的影響。通過仿真實例驗證了該方法的可行性與有效性,為復雜花紋輪胎干濕路面上的制動距離仿真預測奠定基礎。

[1] Cho JR,Kim KW,YooW S.Mesh Generation Considering Detailed Tread Blocks for Reliable 3D Tire Analysis[J].Advances in Engineering Software,2004,35:105-133.

[2] Cho JR,Lee HW,YooW S.A Wet-road Braking Distance Estimate Utilizing the Hydroplaning Analysis of Patterned Tire[J]. Int.J.Numer Meth.Eng.,2007,69:1423-1445.

[3] 莊繼德.汽車輪胎學[M].北京:北京理工大學出版社,1997: 285-320.

[4] 程剛,袁文生.子午線輪胎振動特性試驗研究[J].彈性體, 2006,16(4):7-10.

[5] 喬維高,何耀華.車輛運行時輪胎的振動特性[J].農業機械學報,1999,30(2):22-26.

[6] 吳誥珪,葉峰磊.基于制動輪缸壓力的汽車ABS滑移率的計算[J].公路交通科技,2002,19(3):134-136.

[7] Yeoh O H.Characterization of Elastic Properties of Carbon Black Filled Rubber Vulcanizates[J].Rubber Chemistry and Technology,1990,63(5):792-795.

[8] Simulia.Software Corporation,ABAQUS6.8-1(Dcumentation) [G].Abaqus Analysis User's Manual,2008.

[9] 余志生.汽車理論[M].北京:機械工業出版社,2007:96-100.