土壤水中可溶性鹽分離子對電導率的影響分析：以新疆尉犁縣為例

曹 偉

(新疆水利水電科學研究院，新疆 烏魯木齊830049)

土壤以及地下水中水溶性鹽類的定量化分析，是研究土壤鹽分動態、確定土壤鹽漬化程度以及進行鹽漬土改良應用的關鍵環節之一［1］。在描述土壤水中鹽分狀況時，常用的指標是礦化度和水溶液電導率，但由于土壤水中總鹽含量的檢測化驗過程較為復雜且其與水溶液有著密切聯系，故實際應用中通常采用水溶液電導率這一參數來表征土壤水礦化度的實際狀況。水溶液電導率包含了水中鹽分及離子組成等豐富信息，且該參數具有簡便、快捷、可比性強等特點［2，3］。

電導率法測定土壤水礦化度時，溶液中鹽分離子組成、鹽分濃度、溶液溫度和電導池常數等都會不同程度地影響土壤水電導率的大小［4］。在以上諸多影響因素中，許多文獻認為土壤水中的離子組成和濃度對電導率的影響明顯大于其余各因素［3］。

鑒于以上原因，本文在前人研究的基礎上，利用主成分分析法判斷影響土壤水電導率的主成分因子，并研究土壤水電導率與各主成分之間的相關關系，建立土壤水電導率的預測模型，為進一步研究土壤水鹽運移理論提供一種新思路。

1 試驗區概況

試驗區位于新疆尉犁縣西尼爾鎮境內，其地理位置為41°35'～41°37'N，86°09'～86°12'E，海拔高度 895 ～ 903 m之間。試驗區屬暖溫帶大陸性荒漠氣候，多年平均降水量53.3～62.7 mm，集中于6～8月份，且多以大到暴雨的形式出現。多年平均蒸發量2 273～2 788 mm，多年平均相對濕度為45% ～47%，多年平均氣溫10.5℃，夏季炎熱，極端最高氣溫達43.6℃，冬季寒冷少雪，1月份平均氣溫－9.4℃。全年以晴天為主，日照時間長，太陽總輻射633 KJ，晝夜溫差大。多年平均日照時數3 036.2 h，大于10℃的年積溫4 285℃以上，多年平均無霜期188 d。

該區域農田灌溉水為孔雀河河水，河水礦化度1.0～1.1 g/L。土壤水取樣位置采取隨機定位方式，共計取樣點50處。將采集的水樣帶回實驗室，按照相關程序化驗其電導率和鹽分離子組成(主要為HC、Cl－、S、Ca2+、Mg2+、Na+與 K+這7種離子)。

2 主成分分析法

1933年由Hotelling提出的主成分分析(principal component analysis，以下簡稱PCA)利用降維的思想，把多指標轉化為少數幾個不相關的綜合指標的一種多元統計分析方法，從可觀測的顯式變量中提取信息，組成不能直接觀測的隱含變量。所采用的主要原則是使方差最大，不改變樣本的數據結構，盡可能多地保留原變量所包含的信息，同時用盡可能少的主成分替代原有變量，從而使問題簡化，其主要步驟［5，6］如下:

(1)原始指標數據標準化

假設有n個土壤水樣本，有p項評價指標，可得數據矩陣X=(Xij)n × p。其中:i=1，2，…，n;j=1，2，…，p;Xij為第 i個樣本的第j項指標值。為消除量綱的影響及數量級差別，可用Z－score法對數據進行標準化變換:

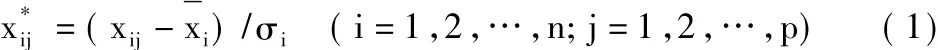
式中:xij為第i個指標在第j個樣本點的原始數據;xi和σi分別為第i個指標的樣本均值和標準差。

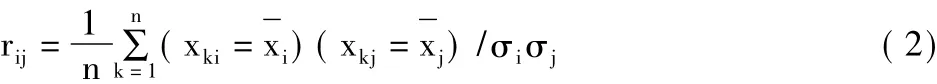
(3)計算特征值與特征向量，根據特征方程|λI－R|=0，求出特征值 λi(i=1，2，…，p)，并使其按大小順序排列，然后分別求出對應于特征值λi的特征向量ei(i=1，2，…，p)，‖ =1要求‖ei，即 表示向量ei的第j個分量。

(4)計算主成分zi貢獻率和累計貢獻率，一般取累計貢獻率大于 85% 的特征值 λ1，λ2，…，λm所對應的第一、第二，…，第m個主成分。

(5)計算主成分荷載。

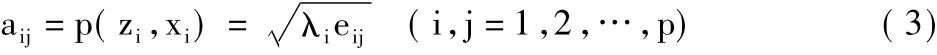
3 模型應用

3.1 主成分分析過程

將50個土壤水樣的鹽分離子與其電導率值進行主成分分析。

將原始數據按式(1)進行標準化后求出相關系數矩陣，見表1。

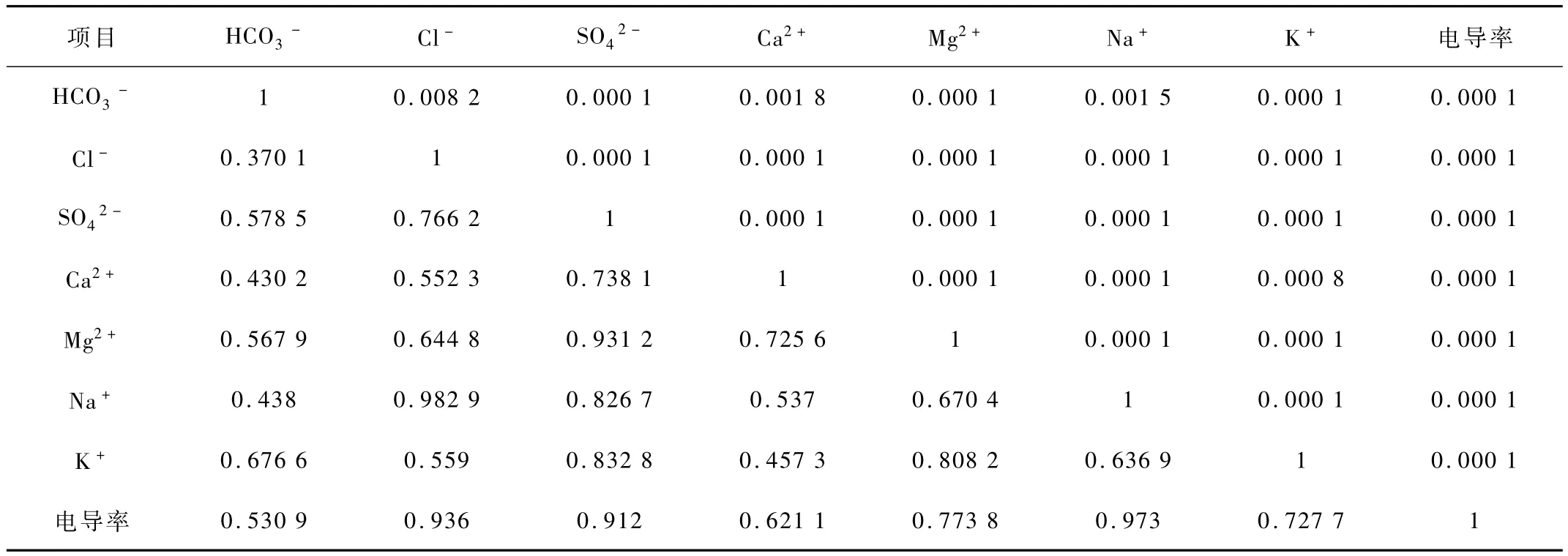
表1 相關系數矩陣

解相關系數矩陣的特征方程以計算特征值，并按上述主成分計算步驟(4)計算特征值方差累計貢獻率(見表2)。按照主成分選取標準確定主成分的個數，根據表2，第一、二、三主成分的特征值分別為 4.978 5，0.866 1，0.609 8，方差貢獻率分別為 71.122%，12.373%，8.711% ，其累計方差率達到了92.206%，說明它們基本包含了以上7個指標的所有信息。其中，第一個主成分又是最重要的，包含的信息最多，對土壤水溶液電導率變化影響最大。

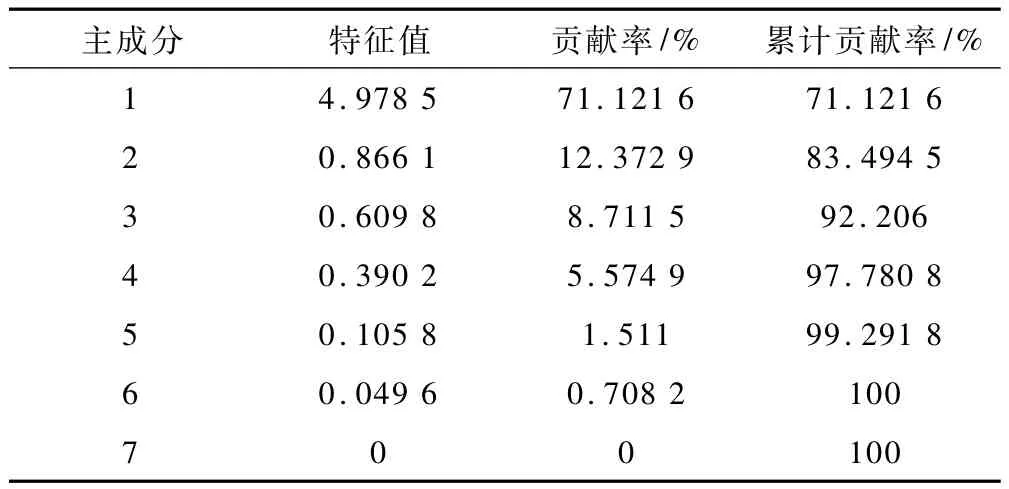
表2 特征值和主成分貢獻率及累積貢獻率

計算各評價指標在主成分中的荷載值(見表3)。從主成分荷載大小來看，與第一主成分密切相關的是Cl－、S、Na+，它們與第一主成分的相關系數絕對值都超過了0.90。與第二主成分密切相關的是HC、K+。在第三主成分中，Ca2+和Mg2+荷載絕對值較高。從方差貢獻率可以看出，第一主成分方差貢獻率71.122%，大于第二、三主成分的貢獻率12.373%和8.711%。所以，電導率主要是由第一主成分，即 由 Cl－、S、Na+控制，其次受控于水溶液中的HC與K+。

對各指標進行KMO檢驗和Bartlett球度檢驗，KMO值為0.612 4，根據統計學家Kaiser給出的標準，適合因子分析;同時Bartlett球形檢驗給出的相伴概率遠小于顯著性水平0.01，因此，應該拒絕零假設，原始變量之間存在相關性，適合進行基本主成分模型的因子分析。

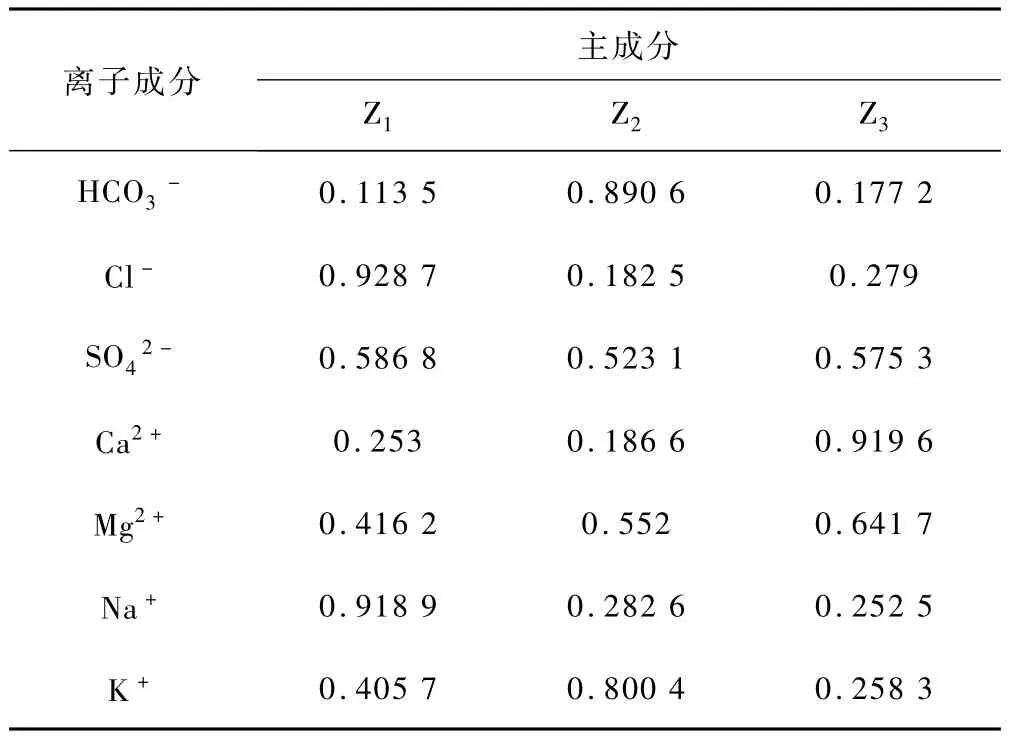
表3 主成分荷載值

3.2 主成分回歸建模分析

在對水溶液鹽分離子與其電導率進行主成分回歸建模之前，有必要先對這7種離子進行多重共線性診斷。目前，在診斷自變量系統中是否存在多重相關性時，經常采用方差膨脹因子(VIF)診斷法［7］。如果 VIFi＞10，表示多重相關性將嚴重影響到系統的模擬值。

針對該系統，水溶液鹽分離子與電導率的共線性診斷結果見表4。

表4 方差膨脹因子

由表4可以看出，7種鹽分離子之間存在較為嚴重的多重共線性，可以用主成分回歸模型來加以分析。

在經過主成分分析與多重共線性診斷后，將3個主成分的得分值代替原來的自變量進行多重回歸分析，得到標準化自變量與因變量間的回歸模型:

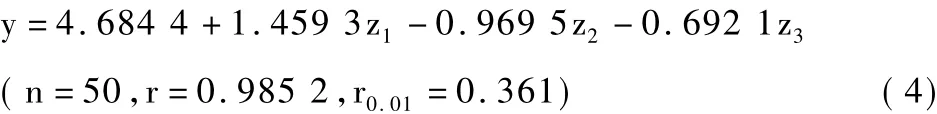
該回歸方程通過了相關系數法的統計檢驗，是可靠的，可以用第一、第二、第三主成分的得分值來對水溶液電導率進行預測，如表5所示，建立的主成分回歸方程，各回歸系數均通過t檢驗，達到極顯著水平。

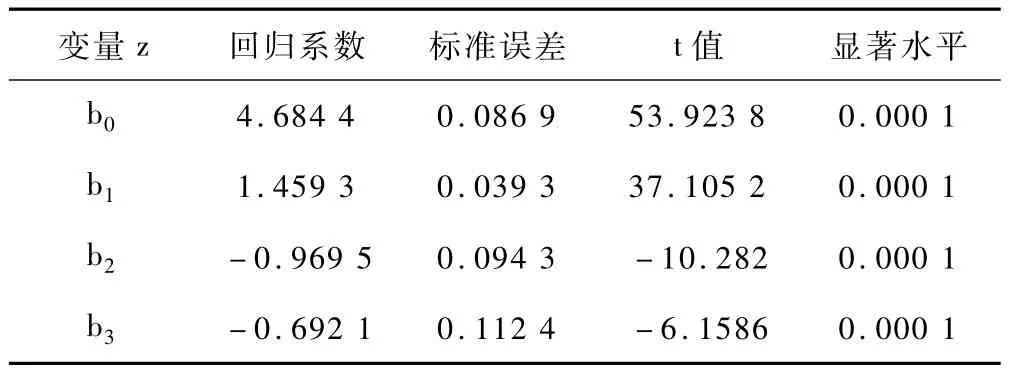
表5 主成分回歸方程系數值

4 結論

1)本文通過主成分分析，得出該區域土壤水電導率主要受 Cl－、SO42－、Na+這3種離子的影響，其次受控于水溶液中的HCO3－與 K+這2種離子。

2)影響土壤水電導率的7種離子之間存在嚴重的多重共線性，應用主成分回歸方法建立電導率的預測模型能夠對水溶液電導率的變化作出精確的預測。

3)土壤水溶液電導率的大小在一定程度上反映其礦化度的大小，但在相同電導率的情況下，由于土壤水中各鹽分離子組成及含量的不同，而導致土壤水礦化度的不同。因此，在研究該區域土壤水鹽運移過程中，有必要專門對Cl－、SO42－、Na+這3種離子的運移做深入研究。

［1］Marshal T J，Holmes J W.Soil Physics［M］.London:Cambridge University Press，1979.

［2］Rhoades J D，Shouse P J，Alves N A.Determining soil salinity from soil electrical conductivity using diferent models and estimates［J］.Soil Sci.Soc.Am.J.，1990，54:46 － 54.

［3］Bhoades J D，Chanduvi F，Leseh S.Soil Salinity Assessment.FAO Irrigation and Drainage Papers，1999，(57):3 －7.

［4］中國土壤學會鹽漬土專業委員會.中國鹽漬土分類分級文集［C］.南京:江蘇科學技術出版社，1989.

［5］馬虹.主成分分析法在水質綜合評價中的應用［J］.南昌工程學院學報，2006，25(1):65 －67.

［6］郭天印，李海良.主成分分析在湖泊富營養化污染程度綜合評價中的應用［J］.陜西工學院學報，2002，18(3):1－4.

［7］劉國旗.多重相關性的產生原因及其診斷處理［J］.合肥工業大學學報:自然科學版，2001，24(4):607 －610.