基于時頻切片分析的故障診斷方法及應用

段晨東，高 強

(1.長安大學 電子與控制工程學院，西安 710064;2.長安大學 汽車學院，西安 710064)

機械設備的故障特征往往被噪聲淹沒，信號具有較強的非平穩性，需要采用有效的時頻分析信號處理方法分離和提取［1］。短時Fourier變換(STFT)、Wigner-Ville分布(WVD)和小波變換(WT)是目前常用的時頻分析方法，在故障診斷中取得了較好的效果［2］。但它們有自身的不足，STFT的窗函數一旦選定，時間和頻率分辨率被固定下來，缺乏細化功能［3］。WVD分析多分量信號時，其交叉項是不可避免的［4，5］。WT的時頻窗口大小是可變的，但其分解和重構依賴小波基函數的選擇，如何根據信號特征選擇基函數仍然是應用中的難題［6，7］。2009 年，Yan［8］提出了一種時頻分析的新方法——頻率切片小波變換(Frequency Slice Wavelet Transform，FSWT)，在汲取STFT和WT的優點的基礎上，通過引入頻率切片函數使傳統的Fourier變換實現了時頻分析功能，另外，逆變換克服了小波變換依賴指定小波函數重構信號的缺陷，可以靈活地實現信號的濾波和分割。Yan［8］也從理論上證明了在一定條件下，這種變換可以轉化為 Fourier變換、STFT、WVD、Gabor變換和Molet小波變換。本文為了提取設備的故障特征，提出了基于FSWT的特征提取方法。首先采用FSWT分解振動信號，得到在全頻帶的時頻分布。在此基礎上根據其能量分布，選擇時間和頻率切片區間進行FSWT細化分析，通過分割和重構得到選定區間的時頻特征，有效地獲取了故障的特征信息，在某煉油廠空氣分離壓縮機齒輪箱摩擦故障診斷中取得了較好的效果。

1 基于頻率切片小波變換原理

1.1 頻率切片小波變換［8，9］

設信號f(t)∈L2(R)，若p(t)的傅里葉變換(ω)存在，其頻率切片小波變換(Frequency Slice Wavelet Transform，FSWT)為:

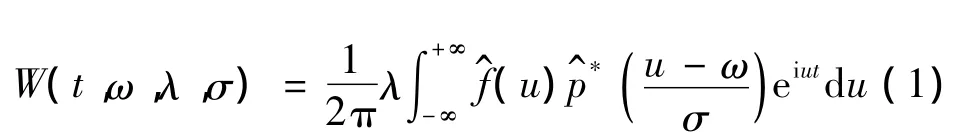
式中:σ為尺度因子(σ≠0)，λ為能量系數(λ≠0)，二者可為常數或為ω和t的函數。在FSWT中(u)是母小波函數p(t)的頻域形式，小波函數是其在頻域伸縮平移的結果(ω)為(ω)的共軛函數。從式(1)可以看出，FSWT拓展了STFT的功能，通過引入尺度和平移因子，獲得了可變的時頻窗，通過引入(·)使傳統的Fourier變換具有了時頻分析的功能。

采用Parseval方程，可以將式(1)轉換到時域:

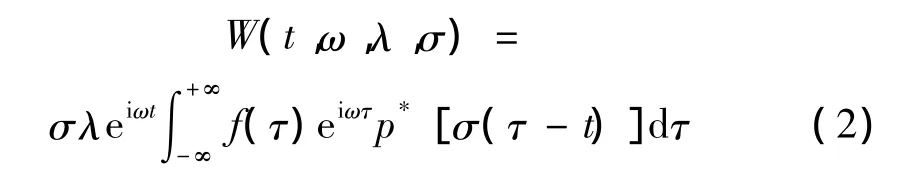
實際上，即使p(t)及(ω)已知，式(2)也難以在頻域上進行分析，因此，在信號分析時僅關注定義為頻率切片函數，它滿足下列條件:

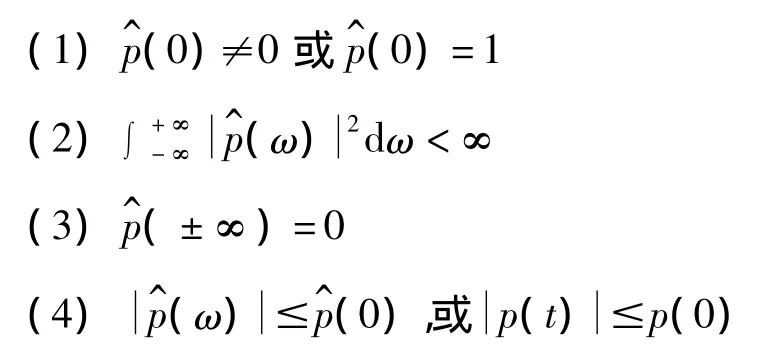
1.2 頻率切片小波變換尺度因子的選擇

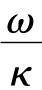
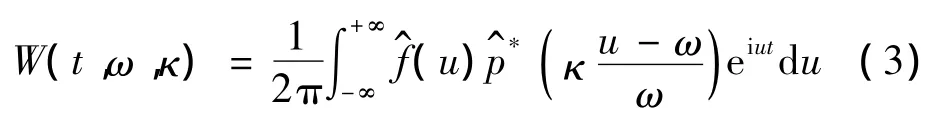
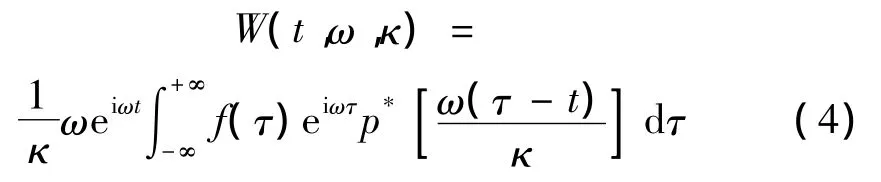
根據Heisenberg不確定性原理可知，同時在時域和頻域得到高的分辨率是不可能的。因此，變換中采用折中方案估計σ和ω，對分析信號引入2個評價系數，一是頻率分辨比率η:

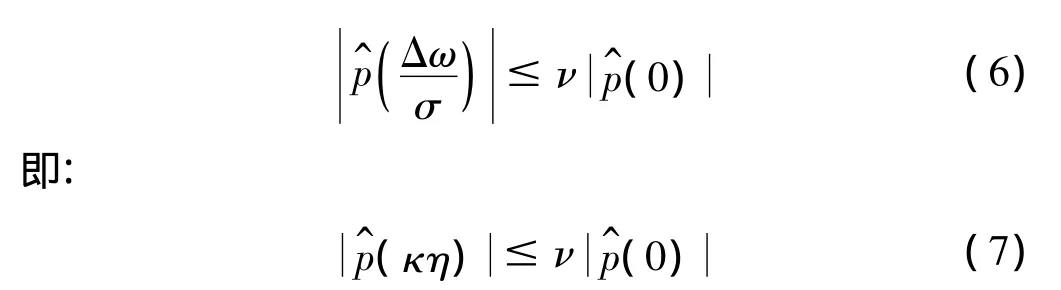
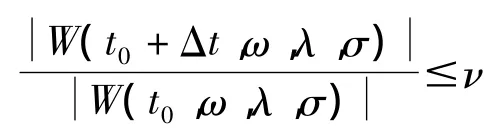
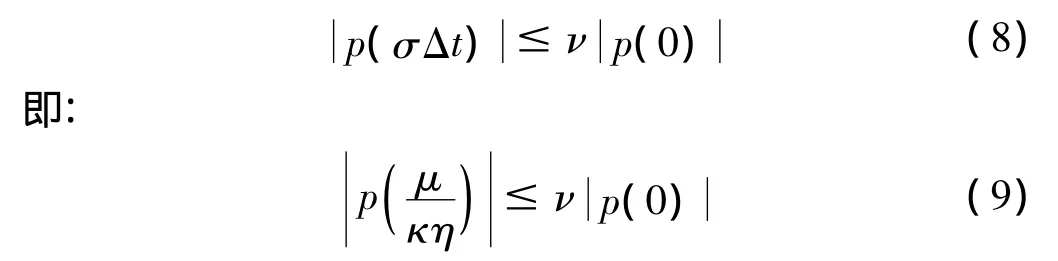
式中μ=ΔωΔt。

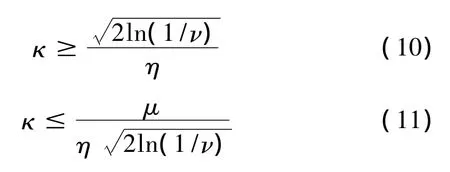
1.3 頻率切片小波變換的逆變換

FSWT實現了信號的時頻分解，由于信號的時域和頻域行為并非獨立的，與連續小波變換一樣，FSWT的結果是冗余的。理論上，逆變換可以采取不同的形式重構原始信號，但FSWT采用其中一種最簡單有效的方式，它的逆變換表示為:

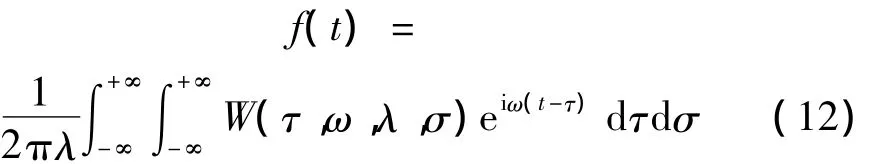
式(12)表明逆變換與頻率切片函數p(t)或p(ω)以及σ無關，重構信號可以直接用快速傅里葉變換算法求得。

2 仿真實驗

設幅值調制信號為:

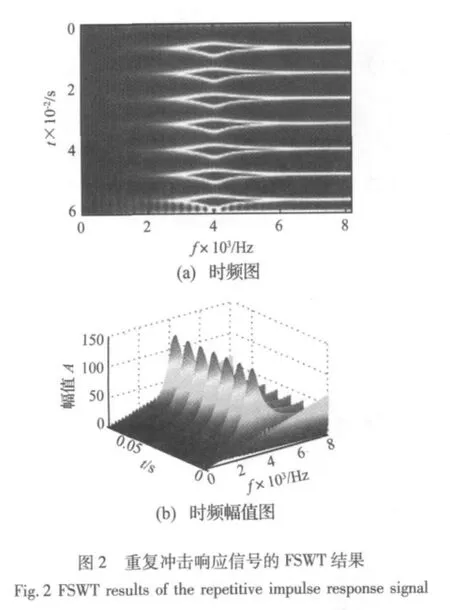
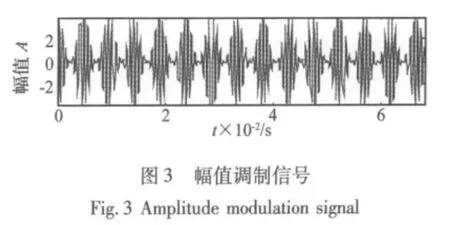
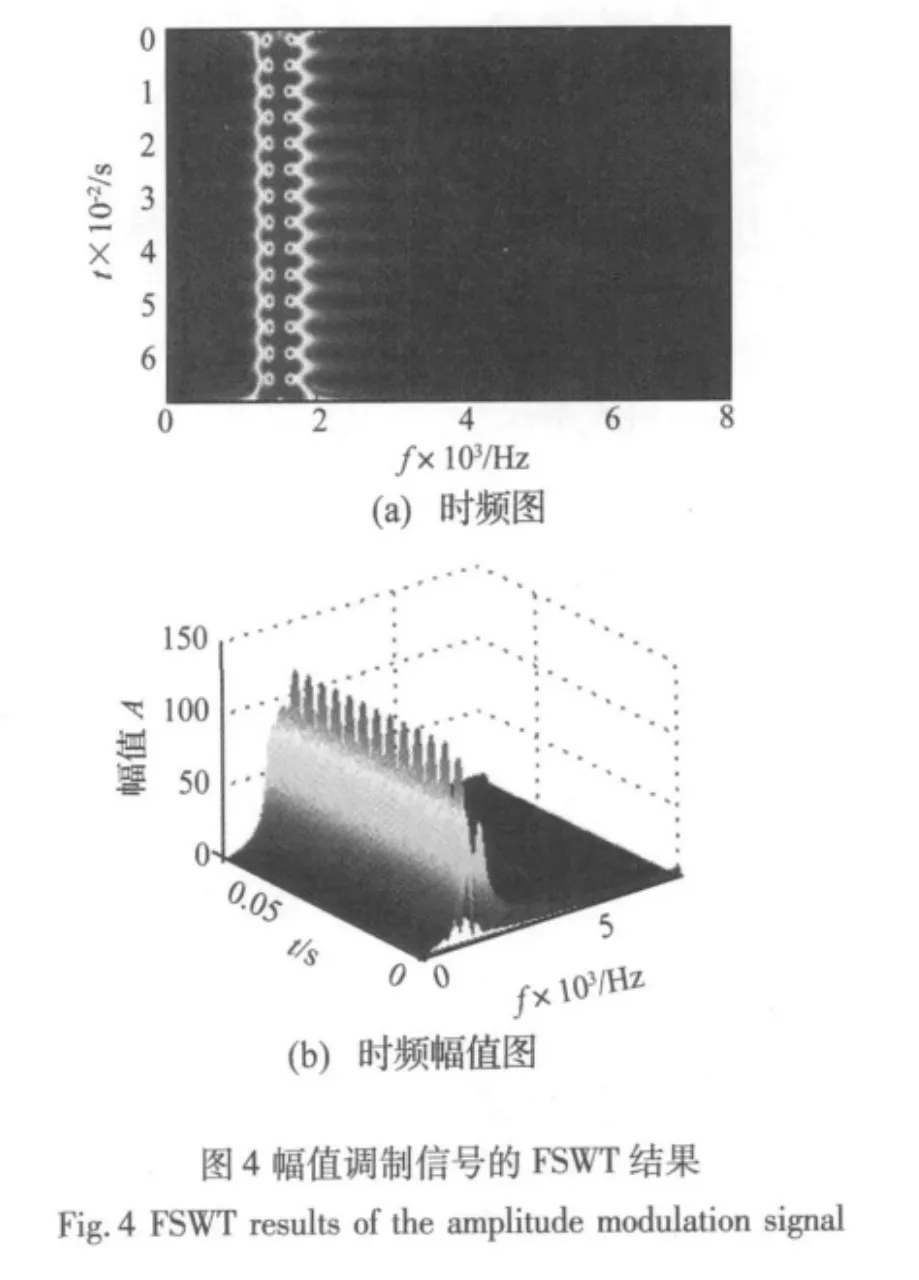
x(t)=［1+cos(2πf1t+ θ1)］［2sin(2πf2t+ θ2)］，其中，調制頻率f1=210 Hz，載波頻率f2=1 500 Hz，θ1=θ2=0°，如圖 3 所示，其采樣頻率為 15 000 Hz，數據長度為1 024。取(ω)=，η =0.05，頻率切片區間取［0，7500 Hz］，圖4為該信號的FSWT結果。從圖4(b)時頻圖可以清楚地看到，在0.068 3 s時間段中，14對的“花瓣”均勻分布在的“主干”上，主干的中心頻率約為1 500 Hz，左右“花瓣”的末端分別對應頻率1 290 Hz和1 710 Hz，它們是幅值調制產生的。“花瓣”個數和持續時間與圖3幅值調制信號的包絡一致。在圖4(b)的時頻幅值圖上也可以發現類似的規律。時頻圖中“主干-花瓣”的形狀準確地描述了幅值調制信號的特點:載波信號在幅值調制信號的作用下，載波信號的幅值隨著調制周期規律地變化著。

3 基于FSWT的時頻分析方法

(1)在選擇合適的頻率切片函數(ω)之后，針對信號特性估算頻率分辨比率η及幅值期望響應比率ν，計算初步的時頻分辨系數κ。

(2)選擇頻率切片區間為信號的Nyquist分析頻帶，對信號進行FSWT變換，求取信號的時頻分解系數W(t，ω，κ)，得到信號在全頻帶的時頻分布圖和時頻幅值分布圖。

(3)根據信號的時頻能量分布，確定細化分析的時域和頻域切片區間。為了獲取故障的重復特征，發現其故障特征的規律，時間切片區間選用信號的整個時間歷程。

(4)對切片區間的信號分量進行分割，采用FSWT變換求取信號在切片區間的細化時頻分布和時頻幅值分布，即分離提取故障特征。為了得到較好的分辨率，可以改變時頻分辨系數κ，增大κ時，時頻分辨率提高。另外，采用FSWT逆變換可獲得切片區間的重構信號。

基于FSWT的時頻分析方法可以同時實現信號時頻分析，可以實現任意頻帶信號分量的濾波和分割。

4 齒輪箱故障的診斷

4.1 故障現象

某煉油廠空氣分離壓縮機組由電機、齒輪箱、壓縮機組成(見圖5)。電機與齒輪箱用齒式聯軸器(聯軸器A)連接，轉速為2 985 r/min(49.75 Hz);齒輪箱為斜齒輪傳動，小齒輪通過止推夾板將斜齒輪嚙合的軸向力傳遞到大齒輪，其回轉頻率為213.00 Hz;壓縮機工作頻率為 213.00 Hz，葉片轉頻為 3 620.86 Hz和4 472.83 Hz。機組某次大修后，齒輪箱振動劇烈，并伴隨尖叫聲。

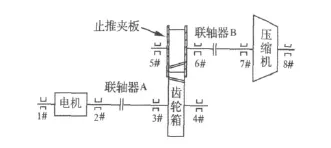
圖5 壓縮機組結構簡圖Fig.5 Schematic diagram of the compressor unit

4.2 故障分析與診斷

為了探究故障產生的原因，用加速度傳感器分別測量齒輪箱的3#、4#、5#、6#軸承座振動。圖6是5#軸承座的一組振動信號及其頻譜，采樣頻率為15 000 Hz，數據長度為1 024。振動信號表現為強烈的高頻振動，在1 480 Hz、2 960 Hz和4 231 Hz處出現較為集中的譜峰，其邊頻帶為213Hz，該值與高速軸的工頻相同。但原始振動信號未發現幅值調制的現象。齒輪箱的劇烈振動主要是由這3個頻率引起的，但它們與機組的嚙合頻率、風機葉片轉頻不對應。

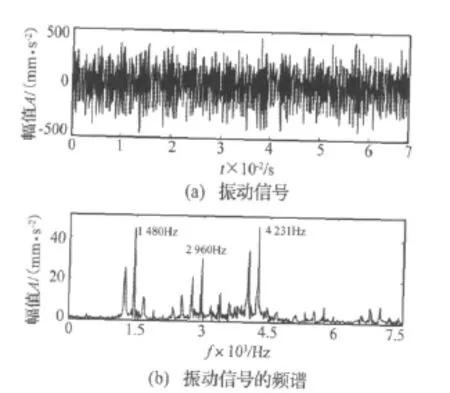
圖6 齒輪箱5#軸承座振動信號和頻譜Fig.6 Vibration signal and its spectrum of#5 bearing brush on the gearbox

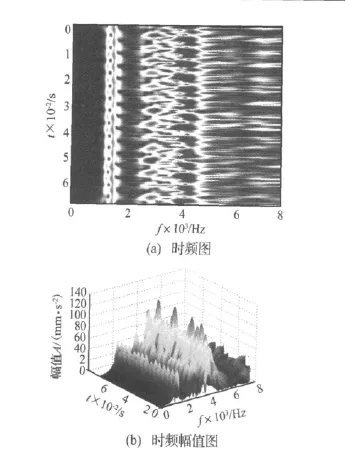
圖7 振動信號的FSWT分解結果Fig.7 FSWT decomposition results of the vibration signal

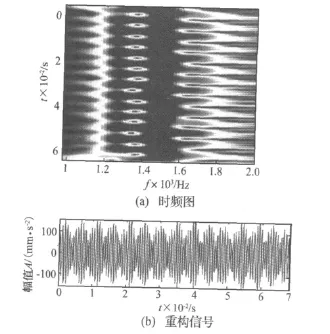
圖8 頻率切片區間［1 000 Hz，2 000 Hz］的FSWT細化分析Fig.8 FSWT zoom analysis of frequency slice［1 000 Hz，2 000 Hz］

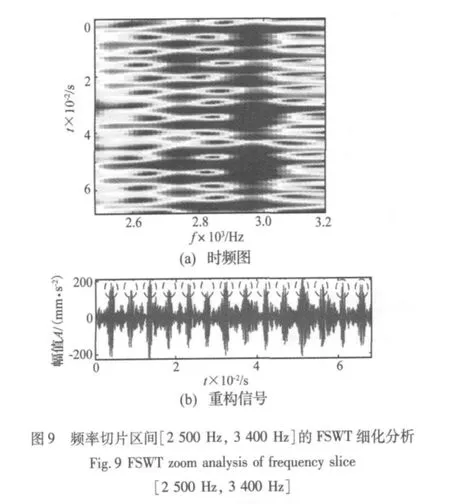
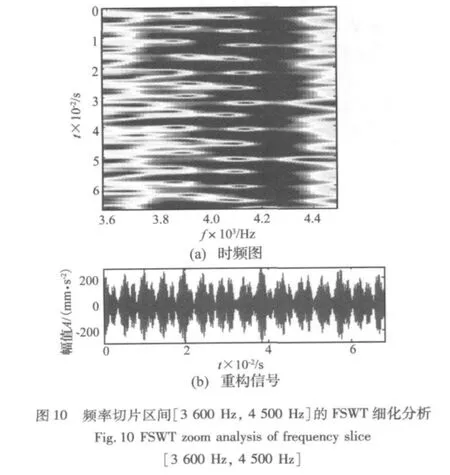
取時間切片區間為取［0，0.068 3 s］，取 η=0.025，對頻率切片區間［2 500 Hz，3 400 Hz］進行細化FSWT分析，得到的時頻圖如圖9(a)所示，時頻圖上14個“色塊”有規律地排列著，間歇出現，窄而強。圖9(b)是重構信號，14個沖擊響應特征清晰可見(圖中圓圈)，時間間隔相同，這說明小齒輪每回轉一次該現象出現一次，齒輪箱在工作過程中受到了周期性的沖擊。在同樣的時間切片區間上，對頻率切片區間［3 600 Hz，4 500 Hz］進行細化FSWT分析，得到的時頻圖和重構信號如圖10(a)所示，此時η=0.025。圖10也表明齒輪箱的小齒輪回轉時受到了周期性沖擊。

為了研究故障原因，對機組的結構進行了分析，探明故障是由止推夾板和大齒輪端面的摩擦引起的。該機組使用的齒輪箱是斜齒輪傳動，在設計上采用止推夾板來限制斜齒輪在嚙合時產生的軸向位移。齒輪箱工作時，小齒輪通過止推夾板把斜齒輪嚙合產生的軸向力傳遞到大齒輪，大、小齒輪在其各自的圓周方向以不同的線速度運動，由于相對運動止推夾板和大齒輪端面的接觸部位產生了摩擦。如果安裝時2個端面保持平行，那么摩擦是均勻的，對齒輪箱的振動不會造成過大的影響。若在加工和安裝存在誤差，止推夾板與大齒輪的端面不能保持平行，致使二者端面接觸，那么，小齒輪每旋轉一周摩擦一次，對齒輪箱產生一次沖擊。其次，若B聯軸器不對中，聯軸器會附加一個彎矩，那么在齒輪箱運行中會增加轉子的軸向力，使轉子在軸向產生213 Hz振動。

通過以上分析可以解釋故障現象，端面沖擊性摩擦激發了軸承座的固有頻率，并對轉頻進行了調制，產生了原始信號頻譜中的邊頻帶。

重新檢修裝配齒輪箱，調整B聯軸器的對中狀況，打磨止推夾板與大齒輪的端面，開機后振動明顯降低，尖叫聲消失，故障排除。

5 結論

FSWT通過引入頻率切片函數使傳統的Fourerier變換具有時頻分析功能，可以同時實現信號的時頻分析，以及任意頻帶信號分量的濾波和分割，有效地提取故障特征。在FSWT時頻能量分布圖上，不同特征信號的形式和形狀不同，有利于故障特征及模式的識別。本文提出了基于頻率切片小波變換的特征提取方法，先采用基于頻率切片小波變換分解振動信號，得到信號在全頻帶的時頻分布，再根據其能量分布，選擇與故障特征有關的時間和頻率切片區間進行細化分析，通過分割和重構實現了故障特征的分離和提取，有效地獲取了正確的故障特征，在空氣分離壓縮機齒輪箱摩擦故障診斷中取得了較好的效果，為旋轉機械的故障特征提取提供了一種新的方法。

［1］何正嘉，訾艷陽，孟慶豐，等.機械設備非平穩信號的故障診斷原理及應用［M］.北京:高等教育出版社，2001.

［2］ Jardine A K S，Lin D，Banjevic D.A review on machinery diagnostics and prognostics implementing condition-based maintenance［J］.Mechanical Systems and Signal Processing，2006，20(7):1483-1510.

［3］劉小峰，柏 林，秦樹人.基于瞬時轉速的變窗STFT變換［J］.振動與沖擊，2010，29(4):27-29.

［4］ Chen G，Ma S，Liu M，et al.Wigner-Ville distribution and cross Wigner-Ville distribution of noisy signals［J］.Journal of SystemsEngineering and Electronics， 2008， 19(5):1053-1057.

［5］ Ram P B，Pradip S.A new technique to reduce cross terms in the Wigner distribution［J］.Digital Signal Processing，2007，17(2):466-474.

［6］ Rafiee J，Rafiee M A，Tse P W.Application of mother wavelet functions for automatic gear and bearing fault diagnosis［J］.Expert Systems with Applications，2010，37:4568-4579

［7］ Peng Z K，Chu F L.Application of the wavelet transform in machine condition monitoring and fault diagnostics:a review with bibliography ［J］. MechanicalSystemsand Signal Processing，2004，18(2):199-221.

［8］ Yan Z， Miyamoto A，Jiang Z.Frequency slice wavelet transform fortransientvibration response analysis［J］，Mechanical Systems and Signal Processing，2009，23(5):1474-1489.

［9］ Yan Z，Miyamoto A，Jiang Z，et al.An overall theoretical description of frequency slice wavelet transform ［J］.Mechanical Systems and Signal Processing，2010，24(2):491-507.