基于BP神經網絡的脈沖渦流無損檢測分析

王俊英，馮華勇

（四川工程職業技術學院，德陽 618000）

0 引言

脈沖渦流檢測近年獲得較大發展。與其他檢測技術相比它具有檢測靈敏度高、設備簡單、操作方便、容易實現自動化的特點。脈沖渦流檢測中渦流的影響因素有很多如缺陷的性質、形狀、深度、被檢測材料含雜質情況、被檢測材料的磁導率、電導率等等，其中含有復雜的非線性變量關系。近年很多國家將神經網絡技術用于解決渦流檢測信號特征的識別上，這將使渦流檢測技術在核工業、航空航天業中發揮重大的作用。

1 神經網絡反向傳播算法（back propagation，簡稱BP算法）

1.1 BP網絡基本結構

人工神經網絡是指模擬人腦神經系統的結構和功能，運用大量的處理部件，由人工方式構造的網絡系統。神經網絡理論是一個非線性動力學系統，并以分布式存儲和并行協同處理為特色。它能較好的適應環境、總結規律和完成某種運算。人工神經網絡是一個具有學習能力的系統。通常具有兩種學習方式：有監督學習和無監督學習。前者可利用給定的學習樣本學習模仿，后者則隨輸入信號的情況可自動發現輸入信號的特征。

1.2 BP網絡的學習算法

要使神經網絡產生所希望的行為，必須對其進行訓練，即網絡學習。學習時每條連接都在不斷的調整自己的權值，以使神經網絡的輸出和期望輸出之間的誤差達到最小，學習的效果直接影響到網絡的預測精度。

BP算法的學習過程由正向傳播和反向傳播兩部分組成，可分為四個過程：l）輸入模式由輸入層向輸出層的模式順傳播；2）誤差信號由輸出層向輸入層的誤差逆傳播；3）正向傳播和逆向傳播反復交替進行的網絡記憶訓練過程； 4）趨向收斂的學習過程。BP算法的學習流程如圖1所示。

BP算法有三種數值優化方法為最速下降法、共軛梯度法（Conjugate Gradient Bakpropagation,CGBP）和牛頓法。其中，最速下降算法是最簡單的算法，但收斂速度慢。牛頓法最快需要計算赫森矩陣和它的逆，計算量大。共軛梯度法是二者的折中：它不需要計算二次導數，但仍然具有二次收斂的特性（即有限次疊代后能收斂與二次函數的極小點）。因此采用了CGBP完成網絡訓練。

2 脈沖渦流無損檢測中神經網絡結構設計

2.1 網絡數據的準備以及輸入、輸出層的設計

在設計網絡之前，必須整理好訓練網絡的數據。本文為實現脈沖渦流表面裂紋深度的自動識別，將采用從原始數據中提取的反映表面裂紋深度的特征值作為輸入。

本文實驗分別采用了銅、鋁、鐵、不銹鋼四種金屬試件。如圖2所示的試驗數據是經過小波除噪處理之后的信號。

從圖2中可以看出渦流峰值隨著裂紋深度的增加而增大，與裂紋深度有著強烈的聯系，完全可以表征裂紋深度。

因此本文將以脈沖渦流檢測信號的最顯著特征值即渦流峰值作為輸入。本文訓練集數據如表1所示。

輸出量實際上就是網絡訓練后提供的期望輸出，輸出最能代表系統要實現的功能目標。選擇相對容易，多網絡的精度和訓練時間影響不大。因為要對表面裂紋深度進行定量的識別，因此文中選擇表面裂紋的實際深度作為輸出。

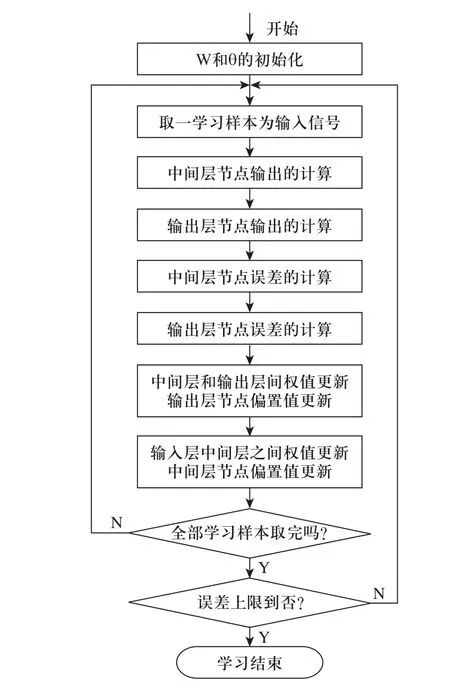
圖1 BP算法流程圖

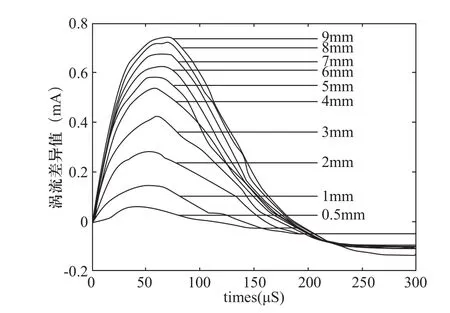
圖2 鋁試件試驗結果

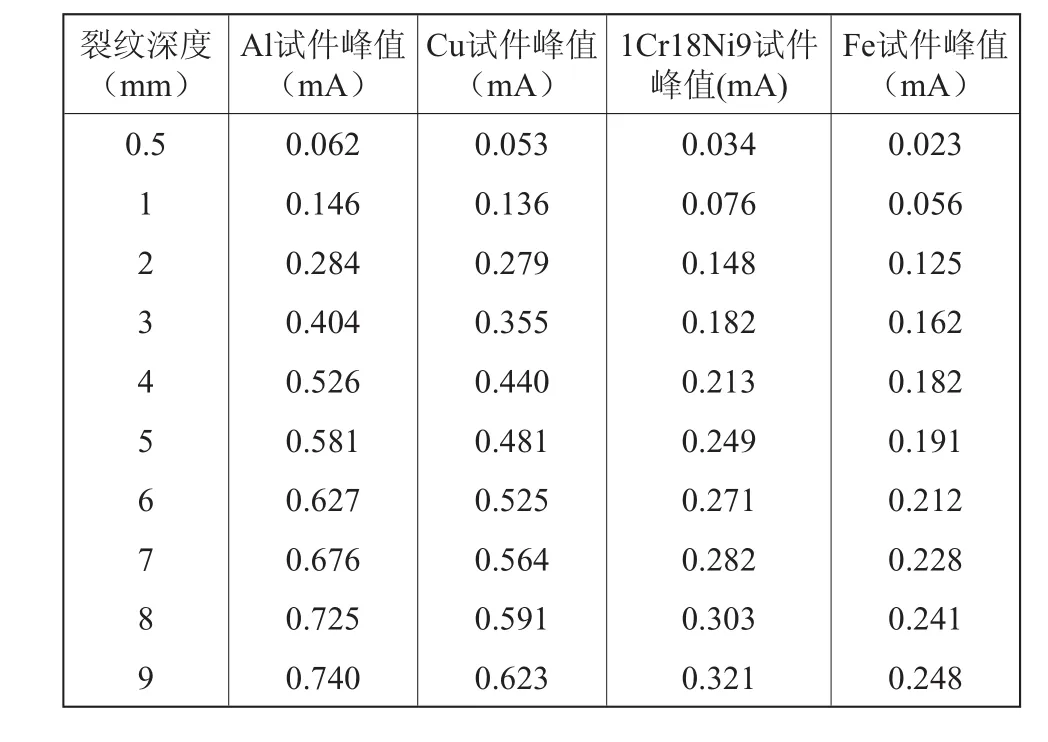
表1 BP神經網絡訓練樣本集

2.2 傳輸函數以及隱含層數和隱含層節點數的確定

由于本網絡的輸入為渦流峰值，輸出為表面裂紋深度，再根據傳輸函數的性質，本文的隱層傳輸函數選擇常見logsig函數即可滿足要求；而因為該神經網絡輸出為非－1和1之間的數值，故輸出層激勵函數選擇線性函數，從而可以輸出表面裂紋深度。

目前對隱含層數和隱含層節點數的確定還沒有通用規則，但經過大量的實踐有幾點結論：對任何實際問題首先只用一個隱含層，使用較少隱含層節點數，然后不斷增加隱含層節點數，直到獲得滿意性能為止，否則再使用兩個隱含層。本實驗隱含層的確定：由于當各節點均采用S型函數時，一個隱含層就足以實現任意判決分類問題。

理論研究已經證明，一個輸入層、一個輸出層、一個隱層的3層BP網絡就可以逼近任何函數[8]。一般而言，增加隱含層數會增加網絡的處理能力，同時也會使訓練復雜化，并使訓練樣本數目和訓練時間增加。所以本課題選擇單隱層結構就完全能夠滿足需要。

隱含層節點數的確定：建立多層神經網絡模型采用適當隱含層節點數是很重要的，往往是網絡成敗的關鍵。隱含層接點數太少，網絡所獲得的解決問題的信息太少，網絡難以處理復雜的問題；隱含層接點數太多，網絡訓練時間急劇增加，且容易是網絡訓練過度，網絡過于處理復雜。

而且，一個網絡要能被推廣，它的可調參數應當與訓練集中的數據點數相當。在神經網絡中，正如在所有建模問題中，要用足以表示訓練集的最簡單網絡。只要有一個更小的網絡能夠工作就不要使用更大的網絡，這就是所謂的剃刀原則。根據本實驗訓練集的輸入、輸出數據對數，根據經驗，我們將隱含層節點數定為3至11個。根據以上所述采用試湊法對隱含層節點數進行確定。經過適當增減隱含層節點數反復試驗比較網絡的預測誤差，發現隱層神經元個數目為6個時，網絡的預測誤差最小，故確定的隱層神經元個數目為6個。

3 表面裂紋深度的自動識別

CGBP神經網絡的參數選擇以下：學習速度初始值一般選擇0.01到0.07之間，學習速度大，收斂速度快，反之則慢：若太大，則有可能修改過頭，導致網絡振蕩、發散等。只有合理的學習速度才提高計算效率．這里值選為0.01，根據實際情況，訓練精度為0.001。初始的偏置值和權值由

MATLAB初始化函數自行得到。然后利用表1所示的激勵樣本做為輸入分別訓練鋁、鐵、銅、不銹鋼四種BP神經網絡，訓練成功后，利用另一組樣本來判別該神經網絡的識別能力，得到裂紋深度的估計值。

3.1 標準試件的擬合結果

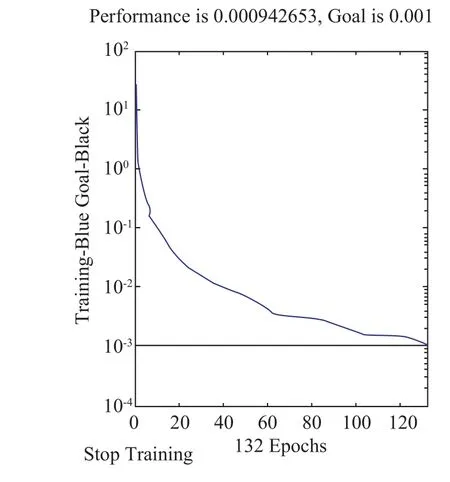
圖3 AI訓練集收斂圖

使用裂紋深度從0.5mm到9mm等10個鋁試件測量得到的渦流峰值作為訓練集，而0.5mm到9mm等10個深度做為神經網絡的目標集。經過若干次迭代后，該神經網絡系統收斂于設計誤差值。其收斂曲線如圖3所示。

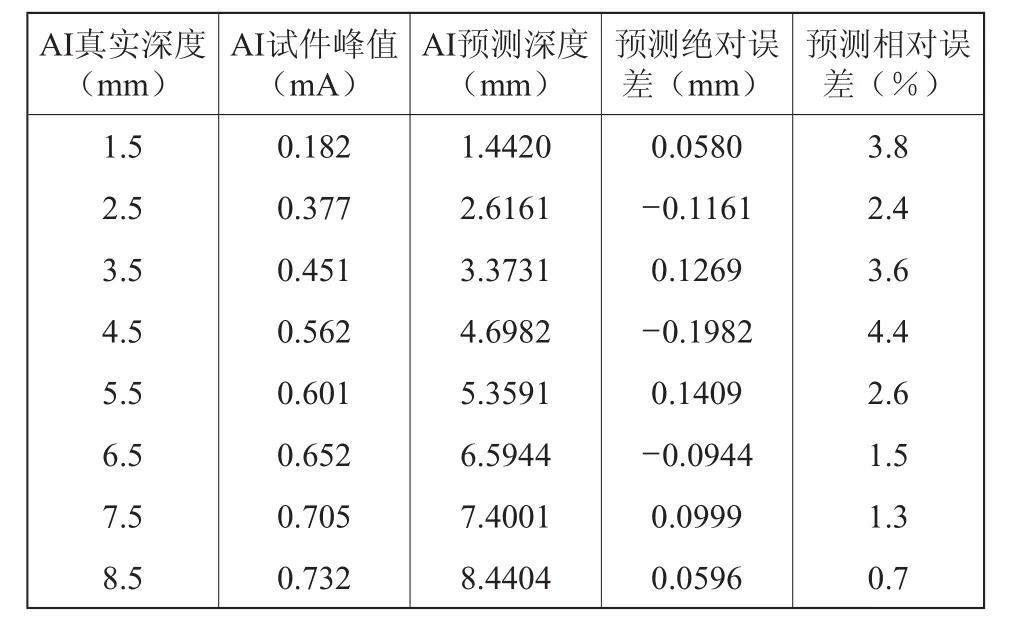
表2 Al測試集擬合結果

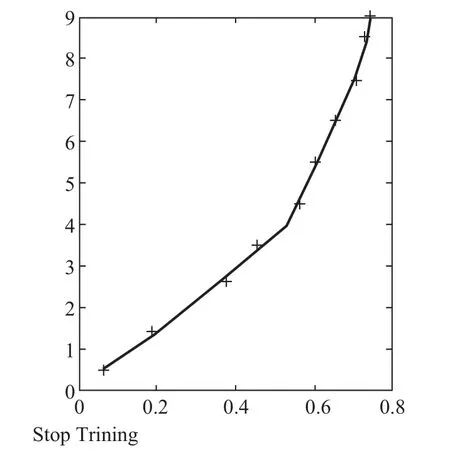
圖4 AI測試集擬合圖

試驗結果顯示訓練成功后的BP神經網絡有著良好的識別能力，能夠較好地根據輸入的AI試件的渦流峰值估計出其對應的裂紋深度。相對誤差均在5%之內，而絕對誤差值都在10-2mm數量級以下，具有較高的識別能力、較好的識別精度。說明應用BP神經網絡對AI試件試驗結果的擬合是成功的。達到了相應的識別精度。估計結果的擬合圖如圖4所示。

3.2 結果分析

試驗結果顯示訓練成功后的CGBP神經網絡有著良好的識別能力，能夠較好地根據輸入的不同材質試件的渦流峰值估計出其對應的裂紋深度。相對誤差均在5%之內，而絕對誤差值都在10-1mm數量級以下，具有較高的識別能力、較好的識別精度。說明應用BP神經網絡對試驗結果的擬合是成功的。但是，要想BP神經網絡保持一定精度要求。就必須保持檢測中的數據的穩定性并取得足夠多的樣本，這樣才能利用神經網絡來定量識別裂紋缺陷的深度值。

但是，由于神經網絡方法是一種隱式的識別方法，其訓練學習花費的時間比較多，學習的收斂速度比較慢，雖然從原理上講，只要隱含層節點數，傳遞函數合適，收斂步數足夠多，采用BP算法訓練的神經網絡可以任意精度逼近任意的非線性系統。但是在實際的網絡訓練過程中，由于BP算法中的搜索范圍越大，局部極小點愈多，從而訓練愈容易限入局部極小點問題的影響，此外，由于受到訓練樣本，計算機數值范圍、非線性作用函數的選取等的影響，BP算法的收斂精度并不令人滿意，有時甚至導致發散。尤其是渦流檢測信號極易受到外界干擾，測得一個比較穩定的值比較困難的情況下，這種情況就更加容易發生。

[1] 孫曉云.智能型渦流無損檢測系統的開發與信號處理的研究[D]. 西安: 西安交通大學, 2000: 3-26.

[2] 聞新. MATLAB神經網絡應用設計[M]. 北京: 機械工業出版社, 2000: 214-296.

[3] 葉子郁. 脈沖渦流檢測系統研究[D]. 四川: 西南科技大學, 2005: 1-28.

[4] 王素菊. 神經網絡在渦流無損檢測中的應用[J]. 南京航空航天大學學報, 1995, 27(5): 697-701.

[5] 幸玲玲, 王東進. 渦流檢測中的組合神經網絡模型[J]. 電子學報, 2002, 30(5): 734-737.

[6] B.Lebrun, Y.Jayet. Pulsed eddy current applications to the detection of deep cracks[J]. Material Evaluation, 1995, 53:1296-1300.

[7] 孫曉云等. 智能型渦流無損檢測儀的研制[J]. 無損檢測,2003, 25(9): 451-455.

[8] Martin T. Hagan. Neural Network design[M], China Machine Press 2002: 1-257.