千米深井巷道嚴重形變測量控制技術

劉娜，欒元重，劉增平，聶文志，閆勇

（1.重慶地礦測繪院，重慶400042；2.山東科技大學，山東青島266510；3.淄博礦業集團山東唐口煤業有限公司，山東濟寧272100）

唐口煤礦開采現狀屬于千米深井開采。由于井下導線點的變形、破壞及巷道修復，巷道在礦圖上的平面位置也發生了變化。因此，此千米深井井下測量工作不僅是多次重復測量導線點坐標，還需及時更新采工圖，確保井下采掘位置與圖紙資料一致。針對這種問題，本文提出采用陀螺定向檢測井下測量控制點穩定性的方法；通過FLAC3D數值模擬及地應變計算，提出了井下巷道變形最小位置；基于GIS平臺開發了井下測量數據管理系統，并實現了采工圖的自動更新技術，確保井下實際位置與圖紙一致，實現安全生產。

1 深井高應力區巷道變形數值模擬

1）模型的建立

依據實際工程地質條件，此模型取了一個具有代表性的垂直剖面，長度為100m，平均深度為1 044m，共劃分成6 000個長1m、高0.5～1m的四邊形平面單元。模型的邊界處理方法是：左右邊界將水平方向的位移置為零，定義為單約束邊界；下部邊界定義為全約束邊界；上部邊界定義為自由邊界。模型計算時采用莫爾—庫侖準則［1］。

2）FLAC3D數值模擬分析

由已知條件建立變形前的巷道模型（如圖1）。巷道開挖以后，巖土體內的天然應力平衡狀態遭到破壞，致使周圍巖土體的應力重新分布，發生變形移動（如圖2）。同時，應力在巷壁附近發生高度集中（如圖3、圖4），導致該區域的巖層屈服進入塑性工作狀態，從而形成塑性區（如圖5），致使應力集中區從巖壁向縱深發展。當應力集中的強度超過圍巖屈服強度時，就出現新的塑性區，如此逐步向縱深發展，形成變形后的巷道（如圖6）［2－3］。

圖1 變形前的巷道Fig.1 Roadway before deformation

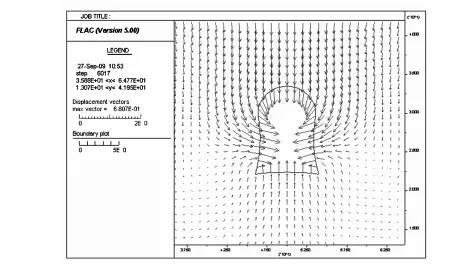
圖2 變形移動Fig.2 Deformation and movement

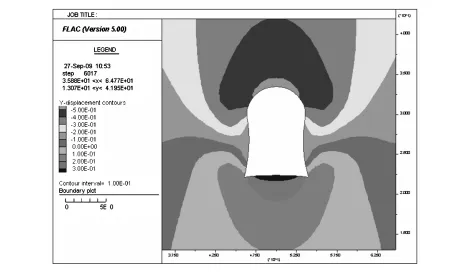
圖3 垂直位移Fig.3 Vertical displacement

由圖7和圖8可以看出，伴隨著兩幫壓力的增高，片幫的產生現象越趨明顯和嚴重。經分析可得，頂壓引起的底板破壞表現為張拉破裂，圍壓引起的底板破壞屬于剪切破壞。此巷道底鼓量較大，導致巷道兩側不平，嚴重者將使混凝土底板發生強烈破壞。因此，井下測量控制點應該布設在拱頂兩側位置，即巷道最小變形位置［4］。

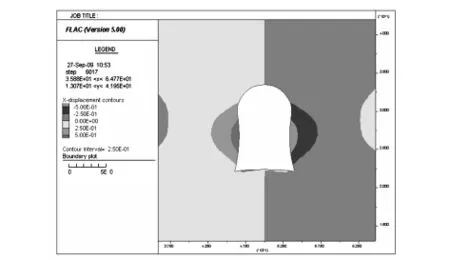
圖4 水平位移Fig.4 Horizontal displacement

圖5 塑性區分布Fig.5 Plastic zone distribution

圖6 變形后的巷道Fig.6 Roadway after deformation

2 千米深井巷道地應變計算

1）地應變計算公式

圖7 最大主應力圖Fig.7 Maximum principal stress

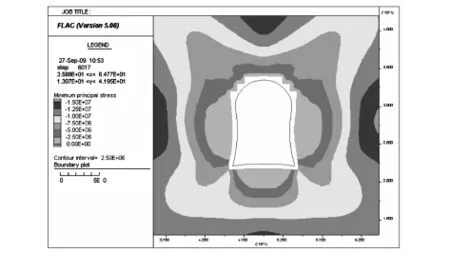
圖8 最小主應力圖Fig.8 Minimum principal stress

用εα表示α方向上線段的線應變，考慮：dx＝Dcosα，dy＝Dsinα并按級數式展開，可得任意方向α上的線應變與該線段平均應變狀態分量之間的關系式：

進一步解得最大主應變ε1和最小主應變ε2為：

彈性力學中已證明：在眾多任意方向上，存在一對互相垂直的特殊方向，經形變后它們只表現為原方向上的長度變化，而直角保持不變，這對軸線稱為主應變軸，其方向稱為主方向。若l、m為主應變方向與縱橫坐標軸的方向余弦，可解得主應變ε1的主方向為：

根據彈性力學中關于剪應變的計算，方向α及90°＋α間的剪應變為：

2）由邊長變化量求地應變

根據以上公式，由2008年8月至2009年8月唐口煤礦南大巷、北大巷、西大巷巷道部分導線的點邊長變化量求地應變，步驟如下：

誤差方程為：vαi＝x＋cos2αiy＋sin2αiz－εαi

利用MATLAB解算可得：x＝247.1885，y＝–426.6845，z＝–607.2942

即：εx＝x＋y＝0.00067mm／m，εy＝x－y＝–0.00018mm／m，

γxy＝2z＝–0.0012mm／m；

按式（2）計算主應變得：ε1＝0.00099mm／m，ε2＝–0.00050mm／m；

按式（3）計算主方向得：α1＝152°33＇；

按式（6）計算最大剪應變得：γmax＝ε1－ε2＝0.0015mm／m；

按式（7）計算面膨脹得：Δ＝0.0005mm／m。

3 導線點穩定性檢測技術

1）陀螺定向技術：在井下實測導線前，采用陀螺儀測量導線邊的方位角，與原來坐標方位角進行對比，以確定井下導線點的穩定性［5］。

2）變形誤差橢圓法：通過導線兩次實測數據，繪制變形誤差橢圓，由變形誤差橢圓確定點的穩定性。

3）三點相對變形計算

通過選擇擬穩點作為基準點來進行井下測點導線的基準轉換，由變換后基準求得三點相對位移值，見表1。

表1 三點相對位移值Table 1 Relative displacements of three points

由表1，繪出各變形點的相對位移如圖9所示［6］：

由圖9中三點相對位移分析井下此段巷道的穩定性，可以發現該基準點中各點均發生移動，北部點移動大，南部點移動小。此結論可為日后千米深井的巷道治理提供參考依據。

圖9 三點相對位移圖Fig.9 Relative displacements of three points

4 地測空間管理信息系統的開發

因巷道變形使井下導線點坐標發生位移，原采工圖繪制的巷道及測量點的位置已不再準確。所以，千米深井應根據井下實測坐標及時進行礦圖更新。為此，本文開發了煤礦信息化管理系統，其功能如圖10所示［7－8］。該系統可實現井下變形巷道位置的自動更新，此功能在唐口煤礦得到了很好地應用，并指導了礦山安全生產，取得了較好的效果。

圖10 系統整體結構示意圖Fig.10 Schematic diagram of overall structure of the system

5 結論

1）采用FLAC3D數值模擬軟件，模擬了千米深井開采巷道的破壞規律，根據可視化的模擬結果提出了井下測量控制點應該布設在“拱頂”兩側位置，該位置為巷道最小變形位置。

2）運用應變與應力模型，根據巷道測量點的變形量分析計算了千米深井巷道的應變值與面膨脹量。

3）通過采用陀螺定向技術、變形誤差橢圓法、三點相對變形計算等方法準確地確定了千米深井井下導線點的穩定性，為以后的巷道治理提供了參考依據。

4）開發了煤礦信息化管理系統，根據井下實測坐標及時實現了礦圖的自動更新，保證了礦山的安全生產。

［1］ 竇林名，何學秋.采礦地球物理學［M］.北京：中國科學文化出版社，2002.

［2］ 朱建明，徐秉業，朱峰，等.FLAC有限差分程序及其在礦山工程中的應用［J］.中國礦業，2000，9（4）：78－81.

［3］ 來興平，伍永平，蔡美峰.FLAC在地下巷道離層破壞非線性數值模擬中的應用［J］.西安科技學院學報，2000，20（3）：193－195.

［4］ 何滿潮，景海河，孫曉明.軟巖工程力學［M］.北京：科學出版社，2002.

［5］ 煤炭科學研究總院唐山分院.陀螺經緯儀基本原理結構與定向［M］.北京：煤炭工業出版社，1982.

［6］ 王磊，劉力，傅 榮.復雜構造計算機繪圖算法研究［M］.北京：地質出版社，1996.

［7］ 崔洪偉.空間數據結構研究［M］.合肥：中國科學技術大學出版社，1994.

［8］ 李偉生，許云濤，胡啟平.適合共享的面向對象的地理數據模型［J］.武漢測繪科技大學學報，1996，21（1）：46－48.