例談數學應用題在高考中的作用

●鄭 怡 (寧波市第三中學 浙江寧波 315040)

例談數學應用題在高考中的作用

●鄭 怡 (寧波市第三中學 浙江寧波 315040)

數學的應用是數學學科的重要組成部分，是這門學科存在價值的一個具體體現，同時也是數學教育的重要內容．新課程標準指出:“高中數學課程應力求使學生體驗數學在解決實際問題中的作用、數學與日常生活及其他學科的聯系，促進學生逐步形成和發展數學應用意識，提高實踐能力”．在數學高考試題中，應用題是必不可少的組成部分，歷來受到廣大師生的重視．

1 考查要求

能綜合應用所學數學知識、思想和方法解決問題;能理解對問題陳述的材料，并對所提供的信息資料進行歸納、整理和分類，將實際問題抽象為數學問題;應用相關的數學方法解決問題并加以驗證，并能用數學語言正確地表達和說明．

2 考點回顧

浙江省從2004年開始實行自主命題．這幾年來，對應用題的考查一直是比較穩定的，主要集中在概率、排列組合、隨機變量的分布列等內容，題型以一個解答題為主，難度一般屬于中檔題．其中也有對函數、數列、不等式以及解析幾何等高中數學重要內容的考查，一般以選擇題、填空題的形式出現，總體難度不高．

3 命題走勢

筆者預計2011年浙江省數學高考應用題還將以常規的概率應用題為主，可能會結合新課程的部分考點，譬如統計、算法等．

4 典例剖析

例1甲、乙、丙3個人站到共有7級的臺階上，若每級臺階最多站2人，同一級臺階上的人不區分站的位置，則不同的站法種數是＿ (用數字作答)． (2009年浙江省數學高考理科試題)

評注本題主要考查了排列與組合的相關知識點以及分類討論的思想．

例2已知某運動員每次投籃命中的概率都為40%．現采用隨機模擬的方法估計該運動員3次投籃恰有2次命中的概率:先由計算器算出0到9之間取整數值的隨機數，指定1，2，3，4表示命中，5，6，7，8，9，0 表示不命中;再以每 3 個隨機數為一組，代表3次投籃的結果．經隨機模擬產生了20組隨機數:

據此估計，該運動員3次投籃恰有2次命中的概率為( )

A．0．35 B．0．25 C．0．20 D．0．15

(2009年福建省數學高考理科試題)

評注本題考查了獨立重復事件的概率以及隨機數的產生．

例3為了測量山頂M，N間的距離，飛機沿水平方向在點A，B進行測量，點A，B，M，N在同一個鉛垂平面內(如圖1)，飛機能夠測量的數據有俯角和A，B間的距離，請設計一個方案，包括:(1)指出需要測量的數據(用字母表示，并在圖中標出);(2)用文字和公式寫出計算M，N間的距離的步驟．

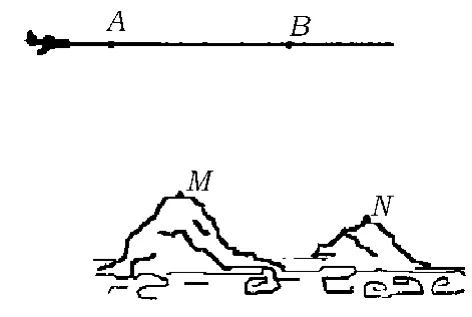
圖1

(2009年寧夏、海南數學高考理科試題)

方案1(1)需要測量的數據有:點A到點M，N 的俯角 α1，β1;點 B 到點 M，N 的俯角 α2，β2;A，B的距離d．

(2)第1步，計算AM，由正弦定理得

評注本題主要考查三角函數的實際應用，思路開闊，答案不唯一．

例45位同學圍成一圈依序循環報數，規定:(1)第1位同學首次報出的數為1，第2位同學首次報出的數也為1，之后每位同學所報出的數都是前2位同學所報出的數之和;(2)若報出的數為3的倍數，則報該數的同學需拍手1次，當第30個數被報出時，5位同學拍手的總次數為＿＿ ．

(2009年福建省數學高考文科試題)

解這個數列的變化規律是:從第3個數開始遞增，且是前 2 項之和，有 1，1，2，3，5，8，13，21，34，55，89，144，233，377，610，987…，分別除以 3 得余數分別是1，1，2，0，2，2，1，0，1，1，2，0，2，2，1，0…．由此可見，余數的變化規律是按 1，1，2，0，2，2，1，0循環，周期是8．在這一個周期內第4個數和第8個數都是3的倍數，因此在3個周期內共有6位同學報出的數是3的倍數，后面6個報出的數中余數是1，1，2，0，2，2，只有1 個是3 的倍數，故3 的倍數總共有7個，也就是說拍手的總次數為7．

評注這樣得到的數列是歷史上著名的斐波那契數列．尋找規律是解決本問題的關鍵．

精題集粹

1．小明中午放學回家自己煮面條吃，有下面幾道工序:①洗鍋盛水2分;②洗菜6分;③準備面條及佐料2分;④用鍋把水燒開10分;⑤煮面條和菜共3分．以上各道工序除了④之外，一次只能進行一道工序．問小明要將面條煮好，最少要用( )

A．13分 B．14分 C．15分 D．23分

2．在20．2℃，細菌受到5%的消毒溶液消毒，每小時細菌的死亡率為11%．在此環境下對一批消毒對象進行消毒，要使細菌的存活率低于原來的5%，消毒時間最少為＿＿ 小時(結果四舍五入精確到1小時)．

3．有一種游戲規則如下:口袋里有5個紅球和5個黃球，一次摸出5個，若顏色相同，則得100分;若4個球顏色相同，另一個不同，則得50分;其他情況不得分．小張摸1次得分的期望是＿＿ ．

4．為了解某班學生喜愛打籃球是否與性別有關，對本班50人進行了問卷調查，得到了如表1所示的列聯表．

表1 學生愛打籃球情況

已知在全部50人中隨機抽取1人抽到喜愛打籃球的學生的概率為

(1)請將上面的列聯表補充完整．

(2)是否有99．5%的把握認為喜愛打籃球與性別有關?說明你的理由．

(3)已知喜愛打籃球的10位女生中，A1，A2，A3，A4，A5還喜歡打羽毛球，B1，B2，B3還喜歡打乒乓球，C1，C2還喜歡踢足球．現從喜歡打羽毛球、喜歡打乒乓球、喜歡踢足球的女生中各選出1名進行其他方面的調查，求B1和C1不全被選中的概率．

臨界值表2供參考．

表2 臨界值

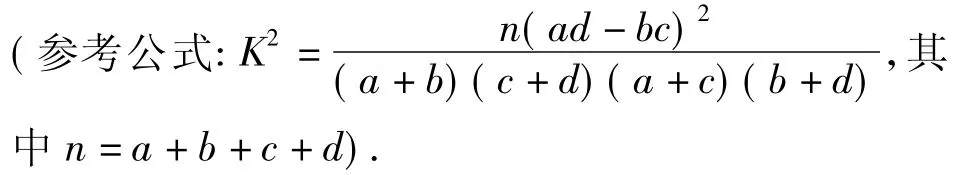
參考答案

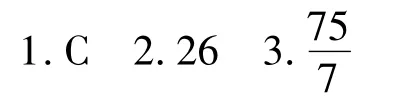
4．(1)列聯表補充如表3．

表3 學生愛打籃球情況

(2)因為