領悟數學思想 提升解題能力

●陳伊遐 (鄞州高級中學 浙江寧波 315194)

領悟數學思想 提升解題能力

●陳伊遐 (鄞州高級中學 浙江寧波 315194)

學生往往容易掌握數學方法，但缺乏對數學思想的關注．而運用數學思想解題既沒有針對特定的數學內容，也沒有固定的解題模式，是在掌握數學本質基礎上的靈活運用．因而，教師在平時的數學教學中應積極滲透數學思想，以逐步深入的方式使學生領悟數學思想，進而提升學生的數學解題能力，培養學生的創新能力，真正減輕學生的學業負擔．中學數學中常見的數學思想有:數形結合思想、分類討論思想、函數與方程思想、整體思想、化歸思想等．

學生普遍感到2010年浙江省數學高考試題比往年難，主要原因是出現了一些新穎的題型，而涉及內容并未超出考試大綱．由于缺乏對數學思想的領悟，學生對這類題目感到束手無策．下面以2010年浙江省數學高考試題為例，闡述數學思想在解題中的運用．

1 數形結合思想

數形結合思想是將抽象的代數與直觀的圖形建立聯系，使抽象思維和形象思維結合，通過對數形的轉化，利用幾何的直觀性，使數學問題化難為易．數形結合思想可以培養學生思維的靈活性、形象性．

(2010年浙江省數學高考試題)

解設x+y=b，則有y= －x+b，即為圖1中一族斜率為－1的平行線，其中b為直線的截距．由x+y的最大值為9知，這族平行線中最上方的一條直線方程為x+y=9，易求與直線2x－y－3=0的交點為(4，5)，顯然點(4，5)在直線 x－my+1=0上，代入解得m=1．故選C．

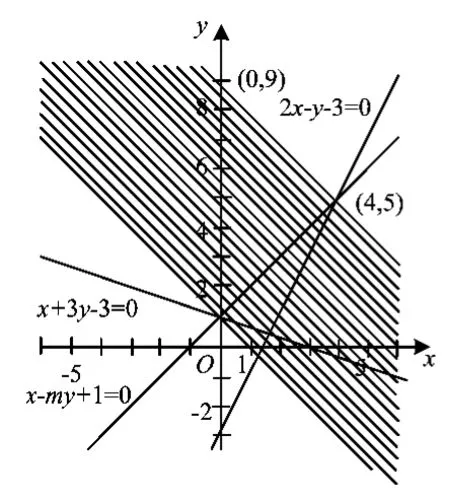
圖1

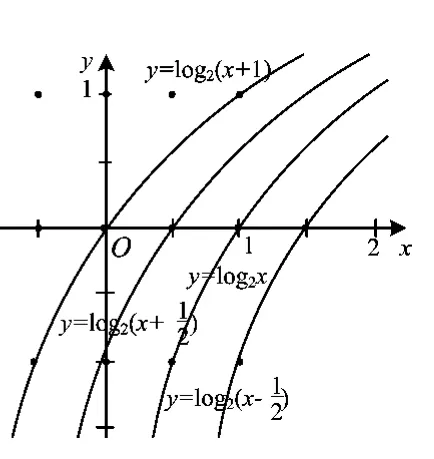
圖2

反思理解式x+y=b中b的幾何意義，借助幾何圖形，例1中線性規劃問題就不難解決．例2中的函數問題顯然可畫圖解決．

2 分類討論思想

分類的對象需是確定的，標準應同一的、不遺漏、不重復．明確討論對象，確立分類標準，正確分類，然后分別加以討論．分類討論是解決問題的一種邏輯方法，也是一種重要的數學思想．有關分類討論思想的數學問題在高考試題中占有重要的位置，因為它不僅具有明顯的邏輯特點，而且能訓練思維的條理性和概括性．

反思本題對a及x4范圍的考慮都用到了分類討論思想，例2中先考慮b=0的情形，然后考慮b=－1及b=1的情形，也是分類討論思想的一種體現．可見一道題的解決常常是幾種數學思想綜合運用的結果．

3 函數與方程思想

函數與方程都是中學數學中的重要內容，也是解決數學問題經常使用的數學思想．函數思想就是用運動、變化的觀點，分析和研究具體問題中的數量關系，通過函數的形式把這種數量關系表示出來并加以研究，從而使問題獲得解決．

4 整體思想

在解數學問題時，人們通常習慣于把它分成若干個簡單的問題，然后再各個擊破，分而治之．有時，研究問題若能有意識地放大考查問題的“視角”，將需要解決的問題看作一個整體，通過研究問題的整體形式、整體結構，并注意已知條件及待求結論在這個“整體”中的地位和作用，然后通過對整體結構的調節和轉化使問題獲解，這種從整體觀點出發研究問題的心理活動過程，可以稱為整體思想．由于這種思維具有一定的簡約性和跳躍性，掌握起來有一定難度．整體思想具體可分為整體觀察、整體代入、整體變形、設而不求等，在解題時，要從問題的條件和結論出發，抓住整體結構，使問題化為熟悉的數學模型，從而解決問題．

5 化歸思想

化歸是將未知向已知轉化，是一種重要的思維模式，也是解決數學問題的一種重要的思想．正是通過不斷的轉化，把不熟悉的問題轉化為熟悉的問題，把不規范的問題轉化為規范的甚至模式化的問題．轉化有等價轉化與不等價轉化，等價轉化要求轉化過程中前因后果是充分必要的，不等價轉化的過程則是充分或必要的，因而需對所得結論進行必要的修正．如例3中，由