一種基于時空擁擠度的應急疏散路徑優化方法

李清泉，李秋萍，2，方志祥，2

1.武漢大學測繪遙感信息工程國家重點實驗室，湖北武漢430079；2.時空數據智能獲取技術與應用教育部工程研究中心，湖北武漢430079

1 引 言

對于諸如鳥巢國家體育館之類的大型公共場所，由于其人員聚集量大，一旦發生突發事件，將會引起很大的人員傷亡［1］。如何將大型公共場所中的人員安全、快速地疏散到安全區域，是國內外許多學者研究的熱點［2］。目前的研究基本上是將人員從室內危險區域疏散到建筑物出口，很少把建筑物疏散和路網疏散結合起來，形成一個完整的疏散方案。為這些大型公共場區域所提供完整的應急疏散方案，能夠使整個疏散過程有條不紊，減少疏散過程中的恐慌情緒，達到提高疏散效率的目的。

目前的應急疏散路徑計算算法，由于各自研究的疏散場景不同，均存在特定的假設和一定程度的局限性［3］。文獻［4］提出的網絡流控制算法是比較經典室內疏散場景的路徑計算算法，該算法能夠提供一個以最短疏散時間為目標的室內疏散方案，從而將人員疏散到最近的出口處。但是該算法需要計算從疏散起點開始到出口的所有可行的路徑，復雜建筑物內部布局環境將使得算法搜索規模膨脹無法控制，導致實效性較差。文獻［3］對文獻［4］的經典網絡流控制算法進行了簡化和改進，通過簡化路網表達方式，計算從起點到所有出口的最短路徑，使得算法效率上得到較大提高。在較大規模路網疏散中，基本都是按照圖論的節點－弧段的方式描述疏散路網，并把車輛疏散問題轉化成多目標優化問題，進而用啟發式算法來解決車輛的疏散路徑分配問題［5－6］。疏散總時間、個體的疏散路徑長度、路徑的復雜度等是常用的優化目標。另外一類解決方法是利用交通規劃中靜態或者動態交通分配的策略來將疏散過程中的交通流分配到路網上［7］。然而，這些應急疏散路徑分配算法，基本上都沒有提供一個從室內危險區域經由路網離開的完整疏散方案。另外，已有的疏散路徑分配算法中，較少有從較細的粒度來分析疏散過程中各個體在時空上擁擠程度以及造成的擁堵。應急疏散的首要目標就是在盡可能短的時間內將危險區域的人員撤離［3，8］。在疏散過程中，一個不容忽視的因素就是疏散過程中的擁堵［5，8］。一旦發生擁堵，整個疏散時間會大大延長，疏散效率大大降低。

2 疏散路網表達

疏散路網代表了疏散個體的所有可達區域［2］。本文疏散研究區域包括了建筑物內部以及周邊的道路網，采用基于圖論的節點弧段方式對疏散網絡進行統一表達。在建筑物內部，節點用來描述房間、走廊、樓梯、大廳等，而弧段則表示這些節點之間的相連路徑［3］。如圖1（a）所示，H1～H5為房間、大廳等室內單元，C1～C8為走廊等單元。對多層結構的建筑物內部，用樓梯等作為節點連接不同樓層。在室外，疏散網絡不僅包括道路，還包括廣場、草坪和人行道等可供行走的區域。將每個可達區域作為節點，弧段表達節點之間的連通關系，室外疏散路網的構建方式如圖1（b）所示。所有節點在本文中統一定義為“疏散通道”。由各個疏散通道之間的連通關系，建立基于疏散通道的疏散網絡G（N，A），N表示網絡中的節點集，A為弧段集。描述為

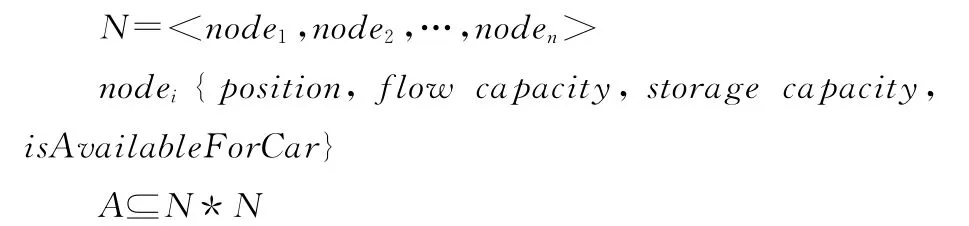
其中，節點的屬性包括其所處位置position、通行能力flow capacity、容量storage capacity以及是否可供車輛行駛isAvailableForCar。通行能力主要由疏散通道在通行方向上的最小寬度決定，限制單位時間內通過該通道的人員或者車輛的數目；容量主要由面積決定，限制疏散通道在某一時刻最多可容納的人員或者車輛的數目。

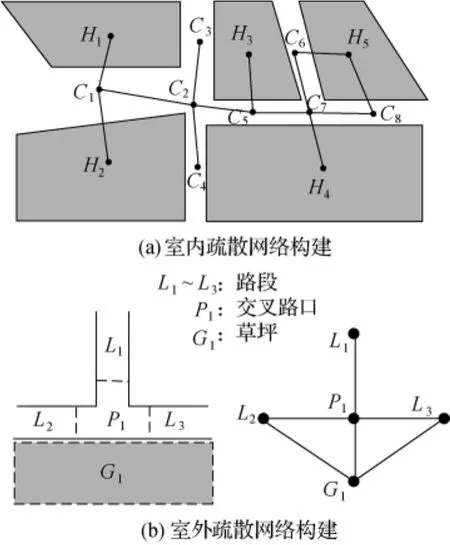
圖1 室內室外疏散通道劃分以及疏散網絡構建Fig.1 Evacuation passage partition and network construction

3 疏散通道時空擁擠度計算

在疏散過程中，被疏散個體會在不同的時刻經過不同的疏散通道并最終到達出口離開危險區域。如圖2，經過路徑1—2—3疏散個體，有不同的時空軌跡。在疏散通道i上以Δt的時間間隔對時空軌跡進行切片，統計在Δt內分配給該通道的人數Ni，換算成小時流率表示疏散通道i的通行能力。Vi／Ci表示疏散通道i在Δt內的飽和度。疏散通道i在Δt內的平均通行速度隨著飽和度的增大而減小。本文采用如下指數函數來描述速度隨飽和度的變化關系

Vmax是疏散通道中自由交通流的速度。當飽和度小于0.5時，通道內行人之間或者車輛之間的相互干擾較小，基本是通暢狀態［10］，因此，平均速度保持自由流速度不變，反之，平均速度隨著飽和度增大呈指數下降。

用f來表示疏散通道在Δt內的擁擠程度。當飽和度大于0.5時，疏散通道內的行人或者車輛開始出現相互擁擠，將這種擁擠定義為時空擁擠度（式（2））。時空擁擠度越大表明疏散通道中的擁堵越嚴重。

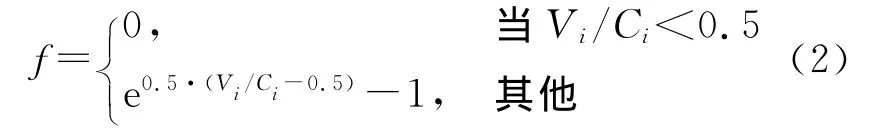
圖2 疏散通道上不同個體的時空路徑分布Fig.2 Time distribution of space－time paths of different evacuees

4 應急疏散方案的生成和優化

4.1 初次分配方案生成

在應急疏散過程中，為了盡快離開危險區域，每個疏散個體都傾向于選擇最短的路徑［1－2］。基于這個原則，初次疏散路徑分配采用k最短路徑算法［9］，針對駕車和步行兩種交通模式，計算從疏散起點O開始到出口D的前k條最短路徑。若是駕車模式，計算的路徑必須經過停車場。兼顧被疏散個體各自的交通模式需求，將k條最短路徑分配給該OD對之間的疏散個體。按照如下的概率為個體m分配疏散路徑n其中，L表示該疏散起點中距其安全出口的最遠距離，T0表示個體的最遲開始撤離時間。

4.2 疏散路徑優化

由于初始分配方案基于最短路徑計算，在實際疏散時會引起比較嚴重的擁堵，主要是由于過多的交通量出現在較短路徑集合上。因此，需要檢測出在路段各自通行能力限制下，時空擁擠度較大的疏散通道。f（i，Δtj）表示疏散通道i上第j個Δt時間切片的時空擁擠度計算值，由函數

式中，ln表示路徑n的長度；fn表示路徑n被分配的次數，fn值越大則分配在該路徑上的疏散個體越多；α、β用于調節ln和fn所占比重。初次疏散路徑分配方案表示為EP＝｛R1，R2，…，Rn｝，Ri為個體i的疏散路徑，n為該OD對之間需要疏散的人員數目。

通過不同氣候帶各稻作區劃(不同生態環境)對稻耐旱性指標的方差分析表明，不同氣候帶和稻區對稻耐旱性各指標的影響達極顯著水平(P<0.005)，表明稻耐旱性表現與氣候環境因素關系密切。

在起點O（房間或者大廳等）的被疏散個體i依據其距安全出口的距離Li，決定其開始撤離時刻f（式（2））計算。

疏散路徑優化之前，需要確定當通道i上Δtj時間內產生擁堵（即f（i，Δtj）＞0.5）時，各通道上重新規劃、分配路徑的人數。具體步驟如下：①計算當f（i，Δtj）＝0.5時，疏散通道i在Δtj能最大能通過的疏散個體數目Nmax；②統計通道i在Δtj內聚集的人數Ni，則需要重新分配路徑的個體數目N＝Ni－Nmax；③將這Ni個被疏散個體按分配的疏散路徑長度降序排列，選擇前N個路徑較長的疏散個體，將其加入到隊列Q＿Replan。

所有Q＿Replan中被疏散個體的初次分配路徑均被清除。在重新分配前，整個疏散網絡各個疏散通道上每個Δt時間切片內的時空擁擠度值均在0.5之內，即疏散網絡處于通暢狀態。Q＿Replan.size表示所有要重新規劃路徑的個體數，G.vexnum為網絡中的節點數目。以Dijkstra算法為基礎，在已有的疏散網絡時空擁擠狀況下為Q＿Replan中的每一個個體m重新搜索最優路徑。步驟如下：

（1）確定m的起始節點和起始時刻，起始節點作為Dijkstra算法搜索的起點。

（2）判斷是否搜索完G（N，A）中所有節點v。如果搜索完畢，就生成一條疏散路徑，否則就繼續擴展搜索節點。

（3）由于存在擁堵，G（N，A）中各個路段的權值不再是靜態的路段長度［11］，由式（4）計算路段綜合權值Wvw

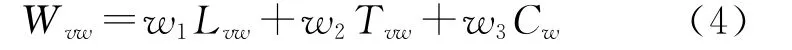
式中，Lvw為節點v到w的長度；Tvw為節點v到w的時間；Cw為節點w上的時空擁擠度值；w1、w2、w3分別為Lvw、Tvw、Cw在路段權值Wvw中所占的權重。Tvw估算方法如下：以m經過節點v的時刻T（v）為起點，統計T（v）＋Δt時間內所有從節點v到w的個體數目Nvw，由式（1）計算節點（疏散通道）v在Δt的平均速度，以此作為m從節點v到w的速度Vvw，則經過w節點的時刻T（w）＝T（v）＋Tvw。將T（w）順序插入到w節點上已有的時間分布序列中，由式（2）計算w節點在T（w）所處的時間片內的時空擁擠度Cw。最終用式（4）可計算出路段權值Wvw。

（4）選擇Wvw值最小的節點w，并將w作為已搜索節點，同時更新當前最優路徑以及該路徑經過w節點的時刻。轉入（2）。

（6）轉到步驟（1），循環計算下一個疏散個體m的重新分配路徑，每一次為m重新計算的疏散路徑均是基于前m－1個疏散個體的時空路徑分布狀況按照式（4）設定的權值計算。直到m＞Q＿Replan.size。新的疏散方案EP＝｛R′1，R′2，…，R′n｝形成。

5 試 驗

5.1 試驗數據

本研究以武漢沌口體育中心體育場及其周邊的路網作為試驗區域。假設在某次大型活動中，由于火災或者某種原因，需要對體育場內看臺上的觀眾進行緊急疏散。由于這種突發的交通擁擠一般出現在體育中心附近區域，因此選擇體育中心周圍的3km左右的范圍作為危險區域，如圖3（a）所示。

圖3 試驗區域及疏散網絡Fig.3 Experiment area and evacuation network

試驗區域中，體育館內部分上層和下層一共42個看臺區。在上層看臺區的觀眾，要依次經過上層看臺出口，到達與上層看臺相連的上層平臺、樓梯、下層平臺、檢票口、通向地面的樓梯到達體育館外部。位于下層看臺區的觀眾，則要依次經過下層看臺出口，到達下層平臺、檢票口、通向地面的樓梯到達體育館外部。其中下層平臺為360°環狀結構，將整個下層看臺區聯系起來。依據體育館的這種內部結構，將體育館上下層空間劃分成一個個獨立的疏散通道，樓梯也作為通道，聯系上下層空間。室外疏散通道的劃分則是考慮了草坪、停車場等區域，將其與現有的道路網整合起來。試驗區域一共包括476個疏散通道。根據這些疏散通道之間的連通關系，建立拓撲網絡，如圖3（b）所示。圖3（b）中①～⑧表示設定的疏散最終出口。室內以及室外草坪、停車場、人行道等行人可達區域通行能力及容量參照文獻［8］計算，車道通行能力參照《道路通行能力理論》設置［12］。觀眾數據為模擬數據，由上座率以及駕車觀眾的比率隨機生成。本文的試驗區域所采用的參數見表1。

表1 試驗區參數數據Tab.1 Experiment parameters

5.2 試驗結果與分析

試驗中，首先針對觀眾的需求（是否需要到停車場取車），基于k最短路徑算法計算每一個OD對之間的k條最短路徑（這里k＝10）。將這一組路徑分配給在該OD對之間的每個觀眾，并根據觀眾的起始位置確定其開始撤離的時刻（最晚撤離時間T0設為180s），形成初始的疏散方案。路徑分配的概率按照式（3）計算，α、β均取1。圖4是部分疏散軌跡在三維時空中的表達，其中紅線標出的軌跡為某駕車的被疏散者從體育館內部疏散到試驗區域出口的完整時空路徑：看臺A（步行）→體育場出口B（步行）→停車場C（取車）→主干道D、E（駕車）→疏散區域出口F。

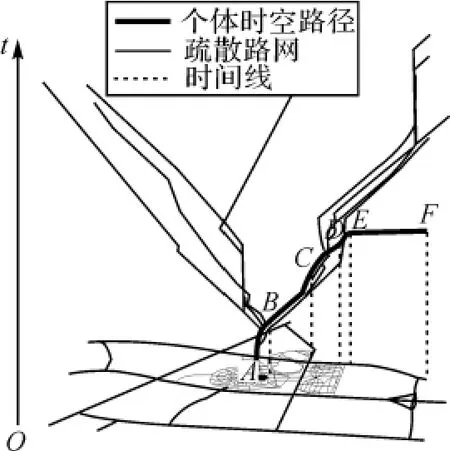
圖4 完整疏散路徑的時空表達Fig.4 Representation of the evacuation paths in time and space

圖5（a）是初次分配方案下，觀眾的時空路徑，每條時空路徑的末端在時間軸t上的投影即為該觀眾的疏散時間。以最短路徑方案為基準，利用本文提出的時空擁擠度計算方法檢測出時空擁擠度較大的疏散通道，最后對一部分觀眾的疏散路徑進行重新規劃、分配，形成一個優化的疏散方案，圖5（b）。其中在分析時空擁擠度時，Δt取20s。在重新計算路徑時，路段權值Wvw的各個項的權重設置為w1＝0，w2＝1，w3＝0，即以時間最短作為優化目標。從圖5（a）和圖5（b）右上角的縮略圖的對比可以看出，優化方案中一部分觀眾重新分配了路徑，利用了路網中擁擠度較小的其他疏散通道，使得總疏散時間更短。本文從以下幾個方面來分析初次分配方案與優化后的疏散方案：

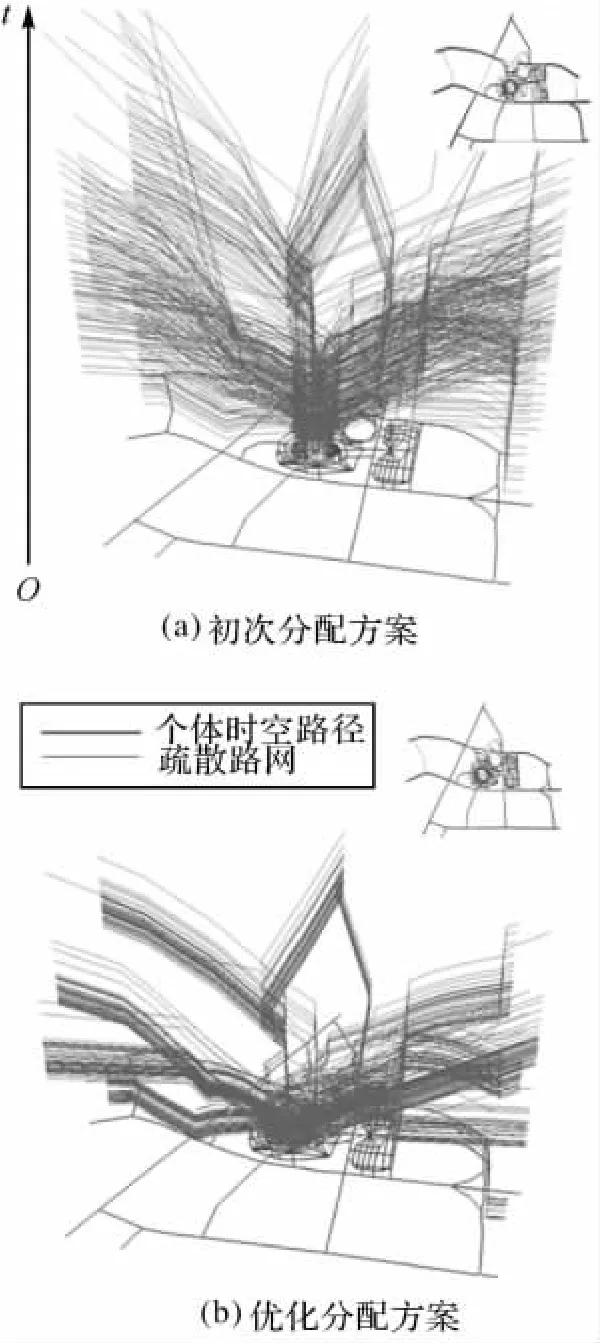
圖5 初次分配方案與優化分配方案時空路徑圖Fig.5 Space－time paths of two route assignment policies

（1）疏散效率比較

評價一個疏散方案優劣的一個重要指標是預期疏散時間。如圖6，優化后的方案，在2 500s左右80%的觀眾就已經疏散出去，而最短路徑分配方案中，由于疏散路網中擁堵嚴重，只有大約20%的觀眾疏散出去。同時，兩種疏散方案的預期疏散時間也相差大約一倍。從表2可以看出，盡管優化后的方案中總的疏散路徑長度大于最短路徑方案，但是在整個疏散效率上，優化后的疏散方案明顯高于初始最短路徑分配方案。在對整個疏散系統的通道利用率上，優化后的方案也是高于最短路徑方案的。由于時間最短是優化的主要目標，在計算疏散路徑時沒有選取過于偏遠的通道，雖然這些通道很通暢，但是整個疏散路徑長度會大大增加，最后增加疏散時間。因此，在優化方案中，通道利用率只是在一定程度上增加。

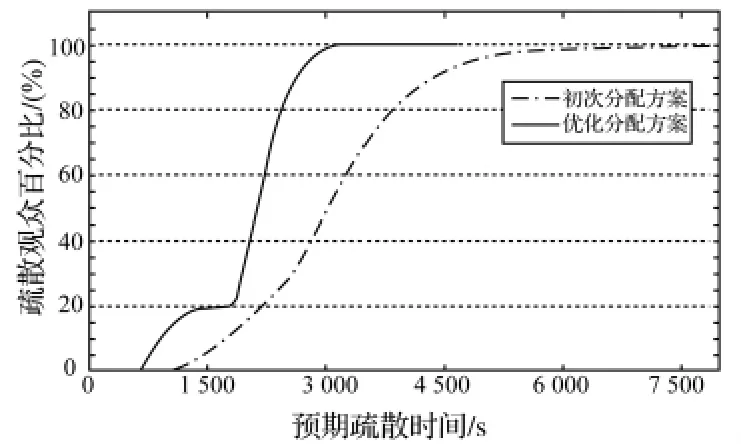
圖6 兩種疏散路徑分配方案的疏散效率Fig.6 Efficiency of two route assignment policies

表2 兩種路徑分配策略的疏散效果比較Tab.2 Evacuation performance of two route assignment policies

（2）整個疏散過程的擁堵狀況比較

以各個疏散通道中Δt＝20s時間片內最大的時空擁擠值作為各個通道的擁堵水平。圖7顯示了各個通道擁堵水平。分為1～5級，5級為最高，1級為最低。從圖7中可以看出，疏散路網中黑色的高擁堵節點減少了。但有部分通道依然擁堵較為嚴重，主要是由于優化時以時間最短作為目標。在計算中權衡路徑長度和所經過的疏散通道的擁堵狀況，經過這些通道的路徑在時間上依然是最優的。表3列出了擁堵等級的分類標準以及兩種分配方案中處在不同擁堵等級中的疏散通道的數量。可以看出，優化后的方案降低了整個疏散網絡的擁堵程度，其中擁堵等級為5的疏散通道數目從52降到40。這40個通道大多數集中在體育場的看臺區，所有觀眾必須從看臺區出口離開，相對狹窄的出口是整個疏散過程的瓶頸。

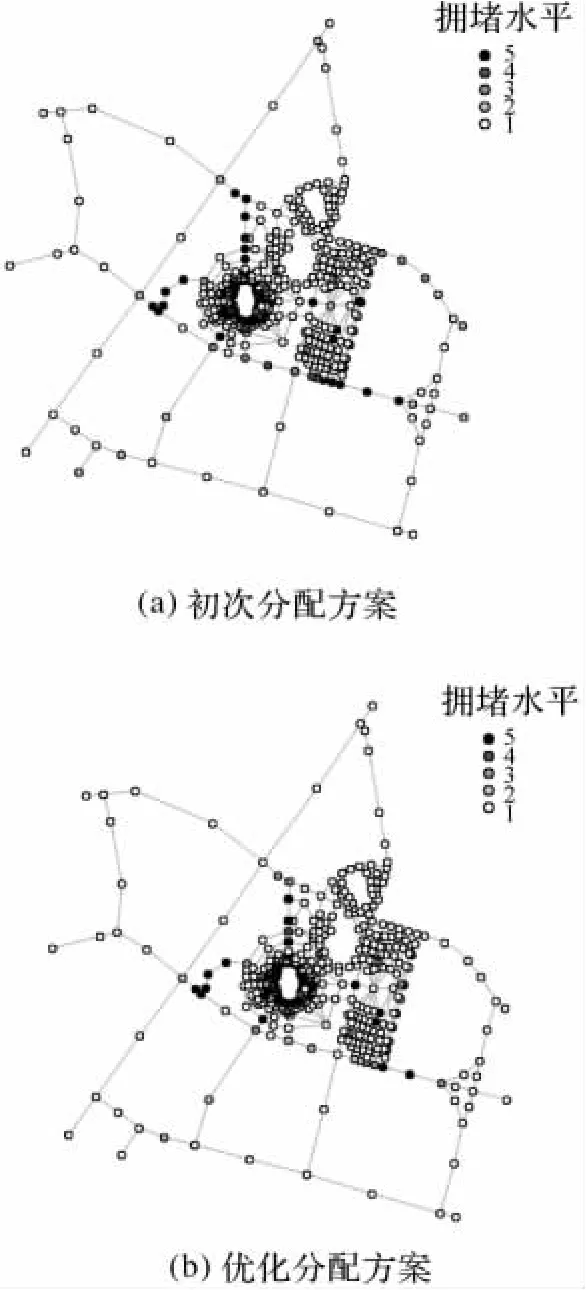
圖7 兩種分配方案下疏散通道的擁堵水平Fig.7 Passage congestion level of two route assignment policies

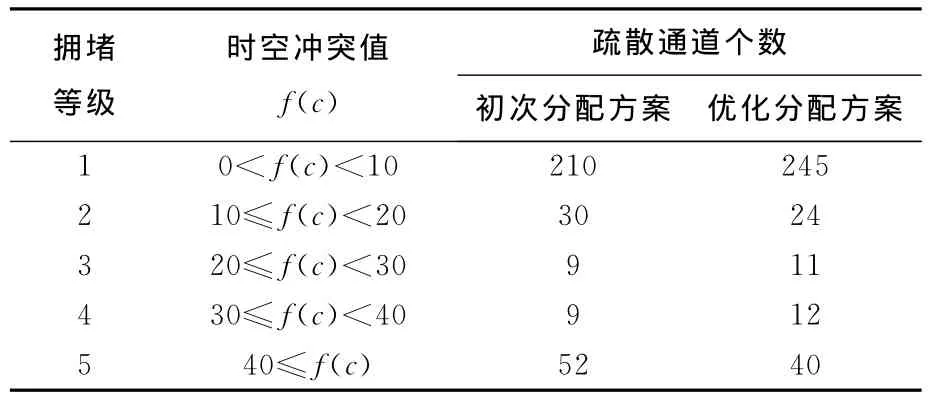
表3 兩種路徑分配方案中不同擁堵等級下的疏散通道分布Tab.3 Evacuation passage distribution under different congestion levels

（3）各個疏散通道在不同的時間切片內擁堵值的對比

圖8表示優化前后每個疏散通道內在Δt＝20s內的時空擁擠值。圖例中灰度以及z軸由小到大表示時空擁擠值由低到高。圖中只顯示了0～ 2 800s的時空擁擠狀況，在2 800s以后，半數觀眾已經疏散出去，各個疏散通道的時空擁擠值明顯減小。對比最短路徑分配方案，優化后的疏散方案能使一些疏散通道的時空擁擠度值明顯減小。

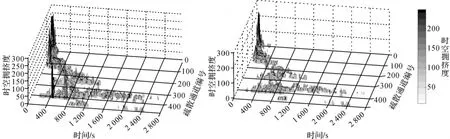
圖8 各疏散通道20s為時間切片的時空沖突分布Fig.8 Space－time congestion distribution by 20stime slice

6 結 論

提出一種基于時空擁擠度的應急疏散路徑分配方法，能夠為大型公共場所人員疏散提供從建筑內部疏散到路網的完整疏散方案。通過分析疏散個體在疏散路網上各個路段上的時間分布狀況，檢測路網中可能出現的擁堵。從減輕擁堵的角度，來建立考慮疏散個體需求的應急疏散路徑分配方法，為每個個體分配一條時空上較為合理的疏散路徑。以武漢沌口體育中心作為試驗區域，對本文提出的應急疏散路徑分配方案進行了驗證。試驗結果表明，經過優化后的疏散方案，能夠緩解以最短路徑為基礎的分配方案中疏散路網上的擁堵，減少整個疏散過程的時間消耗。由于本文提出的優化方法是一個迭代的過程，在優化疏散方案生成的時間效率上有所下降。后續工作將研究如何提高優化疏散方案的生成效率，在動態疏散過程的描述與分析方面進一步進行研究。

［1］ CUI Xihong，LI Qiang，CHEN Jing，et al.Study on Occupant Evacuation Model in Large Public Place：To Consider Individual Character and Following Behavior［J］.Journal of Natural Disasters，2005，14（6）：133－140.（崔喜紅，李強，陳靜，等.大型公共場所人員疏散模型研究：考慮個體特性和從眾行為［J］.自然災害學報，2005，14（6）：133－140.）

［2］ ZHENG X P，ZHONG T K，LIU M T.Modeling Crowd Evacuation of a Building Based on Seven Methodological Approaches［J］.Building and Environment，2009，44（3）：437－445.

［3］ CHEN P H，FENG F.A Fast Flow Control Algorithm for Real－time Emergency Evacuation in Large Indoor Areas［J］.Fire Safety Journal，2009，44（5）：732－740.

［4］ WHITE W W.Dynamic Transshipment Networks：An Algorithm and Its Application to the Distribution of Empty Containers［J］.Networks，1972，2（3）：211－236.

［5］ STEPANOV A，SMITH J M.Multi－objective Evacuation Routing in Transportation Networks［J］.European Journal of Operational Research，2009，198（2）：435－446.

［6］ SAADATSERESHT M，MANSOURIAN A，TALEAI M.Evacuation Planning Using Multiobjective Evolutionary Optimization Approach［J］.European Journal of Operational Research，2009，198（1）：305－314.

［7］ HAN L.Global Optimization of Emergency Evacuation Assignments［J］.Interfaces，2006，36（6）：502－513.

［8］ L?MMEL G，GRETHER D，NAGEL K.The Representation and Implementation of Time－dependent Inundation in Large－scale Microscopic Evacuation Simulations［J］.Transportation Research：Part C，2009，18（1）：84－98.

［9］ EPPSTEIN D.Finding the K Shortest Paths［J］.SIAM Journal of Computing，1998，28（2）：652－673.

［10］ DING Qianfeng.Research on Congestion Pricing of Chongqing Central District［C］∥Proceedings of the 3rd China Annual Conference on Intelligent Transport Systems.Nanjing：Southeast University Press，2007：481－485.（丁千峰.重慶市中心區擁擠收費研究［C］∥第三屆中國智能交通年會論文集.南京：東南大學出版社，2007：481－485.）

［11］ LU Feng.Shortest Path Algorithms：Taxonomy and Advance in Research［J］.Acta Geodaetica et Cartographica Sinica，2001，30（3）：269－275.（陸峰.最短路徑算法：分類體系與研究進展［J］.測繪學報，2001，30（3）：269－275.）

［12］ ZHANG Yaping.The Theory of Highway Capacity［M］.Harbin：Harbin Institute of Technology Press，2007.（張亞平.道路通行能力理論［M］.哈爾濱：哈爾濱工業大學出版社，2007.）