基于參數回歸模型的異步電動機等值電路參數測定
林友杰,謝衛才
(湖南工程學院,湖南湘潭411101)
0 引 言
異步電動機等值電路參數的準確性一直以來都是受到特別關注的問題,也是電機高精度控制必不可少的前提條件。等值電路參數計算的傳統方法是通過空載實驗、堵轉實驗以及直接測量定子繞組電阻實驗和大致估算短路漏抗中的定轉子漏抗分配比例(一般取為相等)來計算出等值電路參數的[1]。
傳統異步電動機參數測定實驗及其處理方法是在近似處理的基礎上建立的。如忽略鐵耗等效電阻,堵轉時s=1,實際運行時一般a<5%,兩者工況不同,由于轉差頻率差別大而使得通過短路實驗所測的轉子電阻與實際電機運行的轉子電阻值不相符;又如數據處理上引入的誤差,等值電路參數計算的傳統方法是通過空載實驗、堵轉實驗以及根據異步電動機的幾種常見類別大致估算短路漏抗中的定轉子漏抗分配比例來計算出等值電路參數的。
電氣工程界,針對電機參數測定的不準確性,采取的措施主要有以下三種[2-8]:
(1)研究更好的實驗方法及數據處理的方法。
(2)利用在線識別參數的技術來得到更符合實際運行時的參數值。
(3)利用模糊控制等控制方法來減弱或撇開對電機參數的依賴性。
文獻[2]研究了更準確的計算模型,利用直接求解方程組的方法得出了更準確的電機參數,但在構建方程組時由于受方程組本身特性的影響,采用了由空載、短路和負載實驗數據組成方程組,雖然較傳統的方法更準確,但由于電機運行時的參數與空載、短路時的參數值有所不同,參數處理精度還可以提高。
本文從參數回歸模型入手,利用異步電動機的負載實驗數據,利用在優化擬合方面功能強大而又簡單易用的1stopt軟件來研究電機參數更準確的處理方法。
1 參數回歸模型
異步電動機的等值電路表現出8個參數,Rs、Rr、Rm、Lls、Llr、Lm及 s、ω,后兩者與運行條件相關,是外部參數,通過簡單計算即可得到,其中ω為給定電源的頻率,s為轉差率,通過ω和轉速來求取(圖1,轉子側參數是已折算到定子側的值)。其它6個參數為異步電動機等值電路的基本參數,是通過實驗直接測定或其它方法間接求取的對象。
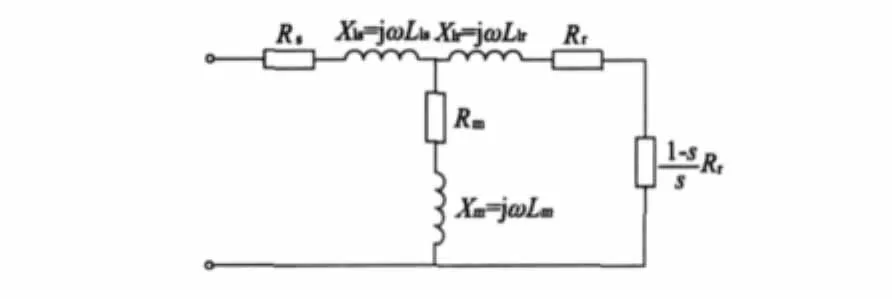
圖1 異步電動機等值電路
從圖1可知,等值電路的輸入阻抗:
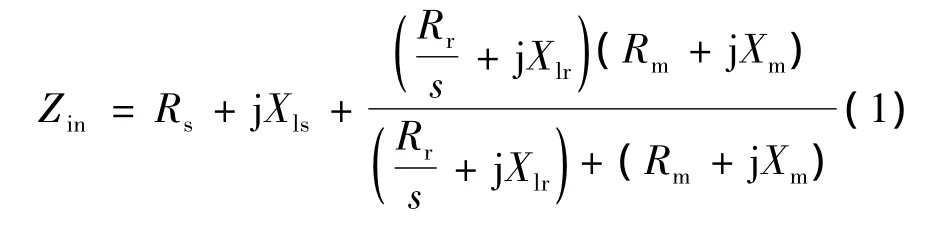
進一步推導可得關于輸入阻抗的實部和虛部的2個方程:
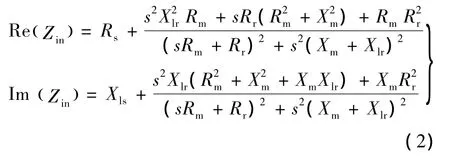
式中:Zin為定子側輸入阻抗,Re(Zin)、Im(Zin)為求Zin的實部、虛部運算。
從電路的觀點看,輸入阻抗的實部和虛部所消耗的功率分別為有功功率和無功功率。這兩部分的功率可以通過功率表、電壓、電流表測出,在忽略電機的機械損耗的基礎上,其值分別為:
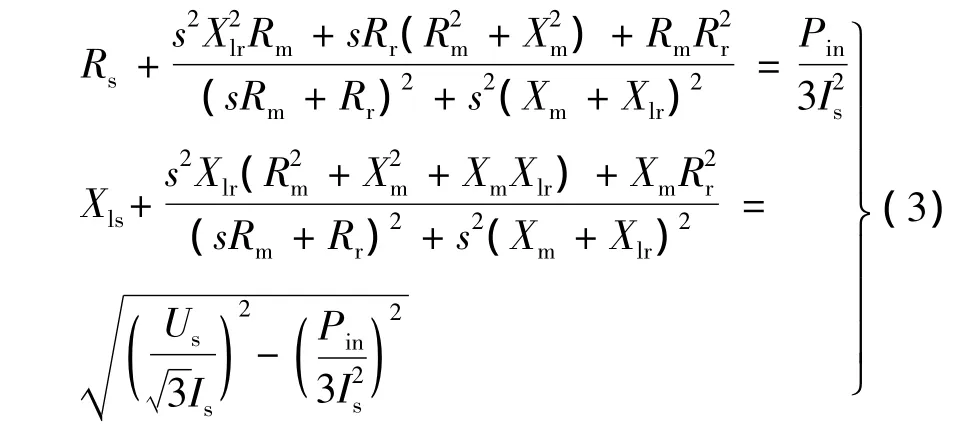
式中:Pin、Us、Is為異步電動機參數測定實驗時的輸入功率、定子線電壓、線電流的測量值。ω為電源角頻率,ω=2πf,f為輸入電源的頻率,轉差率s通過下式計算:

式中:p為電機極對數;n為電機轉速。式(3)就是異步電動機等值電路參數回歸模型,為了計算方便,改寫如下:
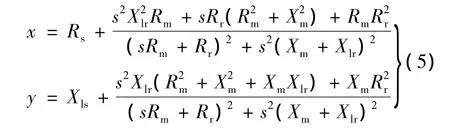
式中:
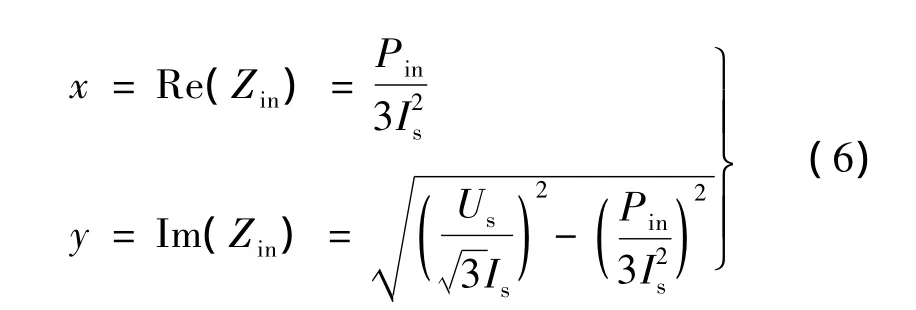
式(5)是異步電動機參數回歸模型(式(3))的計算模型,回歸模型的輸入為s、x、y,待回歸的參數為異步電動機的各電阻、電感的量值。在回歸模型中采用電抗而不是電感作為求解參數,因為考慮到異步電動機中的電抗比電感在數值上更接近于電阻,在非線性方程組上更易于求解。
2 回歸模型的直接求解
利用參數的回歸模型以及異步電動機的負載實驗數據值,可以求出負載時的異步電動機等值電路的參數值。樣機YLEWF-6三相異步力矩電機的負載實驗數據如表1所示。由式(4)、式(6)可以得出參數回歸模型(式(3))所需的 s、x、y值數據,如表2所示。
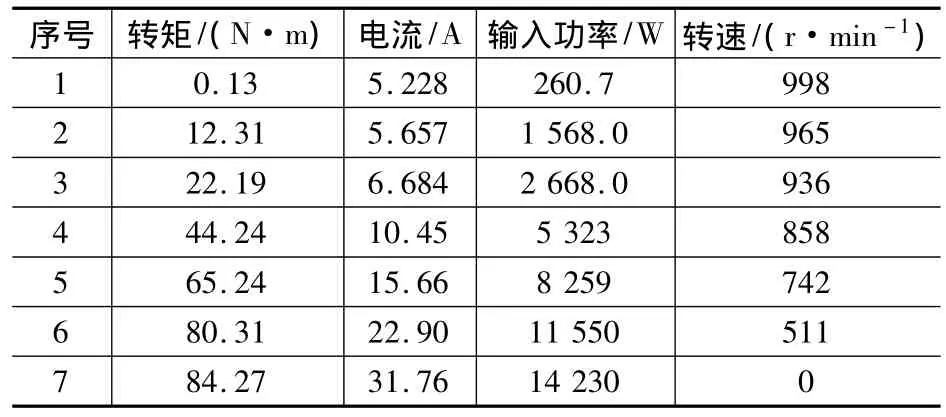
表1 負載試驗數據匯總(定子繞組星形聯結)
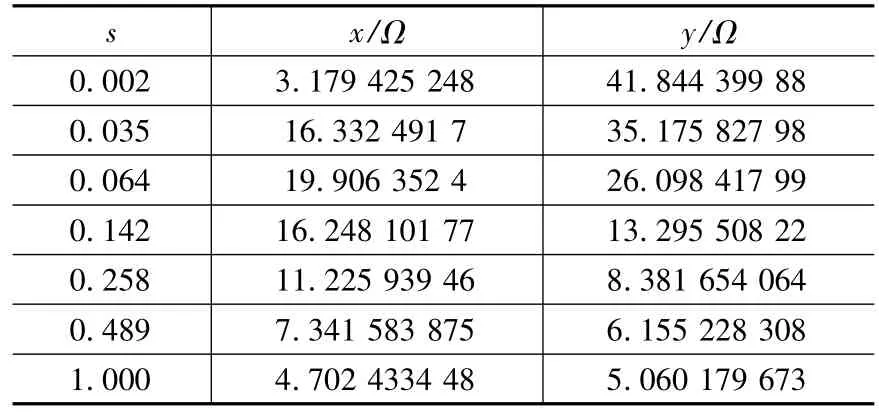
表2 參數回歸模型的數據
將s、x、y作為變量,利用1stopt進行回歸計算得出待擬合的參數值。
數據處理結果如表3所示。
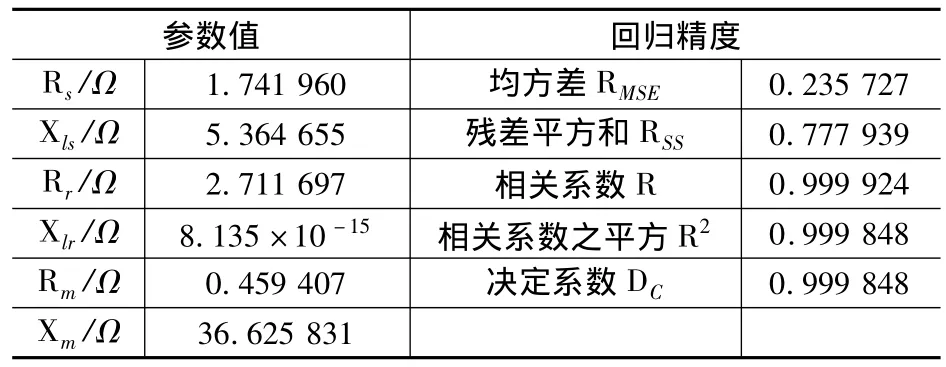
表3 直接回歸方式的參數值和精度
從表3可以看出,回歸的相關系數達到了0.999 8,接近于1。從實際的物理情況看,轉子側不可能沒有漏磁通/漏磁鏈,因此對應的漏抗值就不可能為0。參數中除了轉子的漏抗與實際不符外,其它參數的大小及各參數之間的數量級大小關系符合實際的電機情況。
這個誤差是由定子電流、輸入功率的測量精度以及x、y的計算精度、回歸方程的非線性等引起的。可以將這些影響因素歸結為對s的影響,即認為s的數據是準確的,而將所有的誤差加在轉差率s上。
因此從某種意義上講,可以用變轉差率s(回歸中修正的s值)方法進行回歸擬合,以提高擬合的準確性。借助ParVariable關鍵詞,1stopt可以完成這一過程[9]。
對應的變轉差率s回歸方法的回歸結果如表4所示。
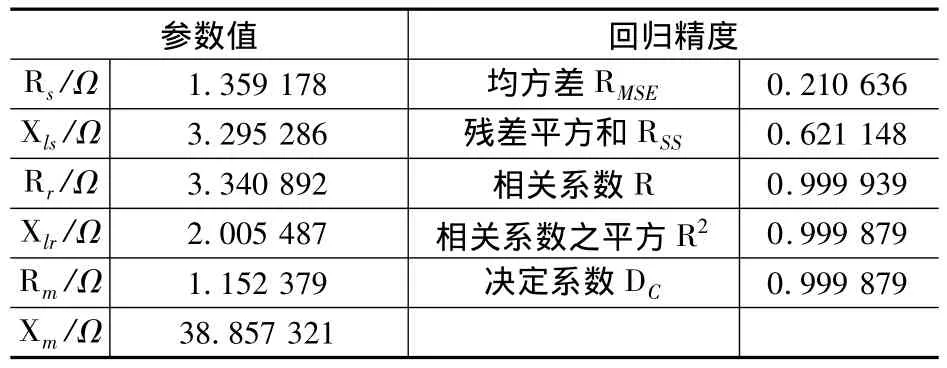
表4 變轉差率s回歸方式的參數值和精度
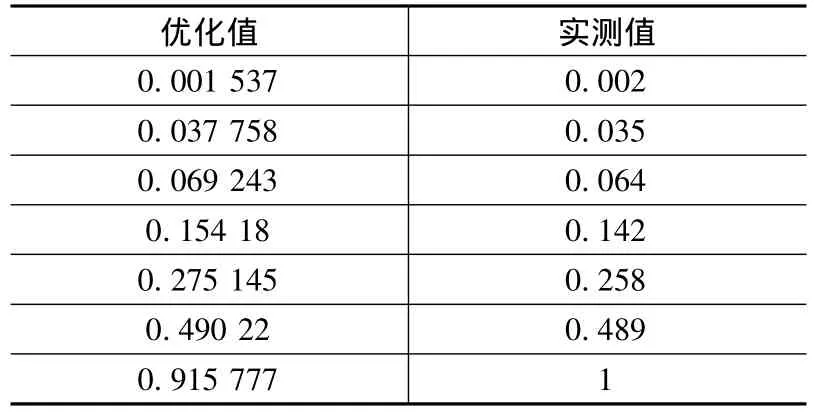
表5 轉差率的優化值和實測值
表4為變轉差率s回歸方式的參數值和精度。表5的第1列數據為變轉差率回歸中的轉差率優化值,表5的第2列數據為負載實驗的轉差率實際值。
從表4和表5可以看出,將誤差的影響集中放在轉差率來考慮而帶來的轉差率的偏差值不大。但轉子側參數的回歸值有了明顯的改善(特別是轉子漏電阻),與定子側的數值相接近且在同一數量級上,這更符合異步電機參數值實際物理情況。是否更接近被測電機的實際參數值,要通過進一步的方程組特性研究和更多的實驗才能得到驗證,這步工作尚需深入。
3 帶約束條件的回歸模型的參數求解
IEEE Standard 112標準中給出了幾種類別的異步電動機的定轉子漏抗(漏感)的推薦值[1]。根據該標準,若大致知道異步電動機的定轉子漏抗比,就可以進行帶約束條件的回歸模型的參數求解。
根據力矩電機的定轉子漏抗參數的分配比例,可得約束條件:

表6為帶約束條件的回歸模型所得出的異步電動機的等效電路參數值及對應的回歸精度。
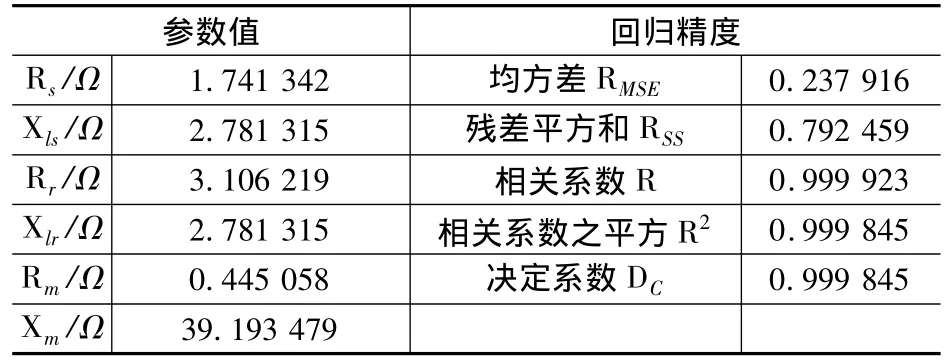
表6 帶約束條件回歸的參數值和精度
從表6可以看出,加入了約束條件,等值電路的參數值符合力矩電機參數值情況。帶約束條件的回歸方法與變轉差率s的回歸方法(表7)相比,可以很明顯地看到,擬合精度稍遜于后者,電機等值電路中的定子電阻值明顯比后者大,而勵磁電阻要明顯小于后者。
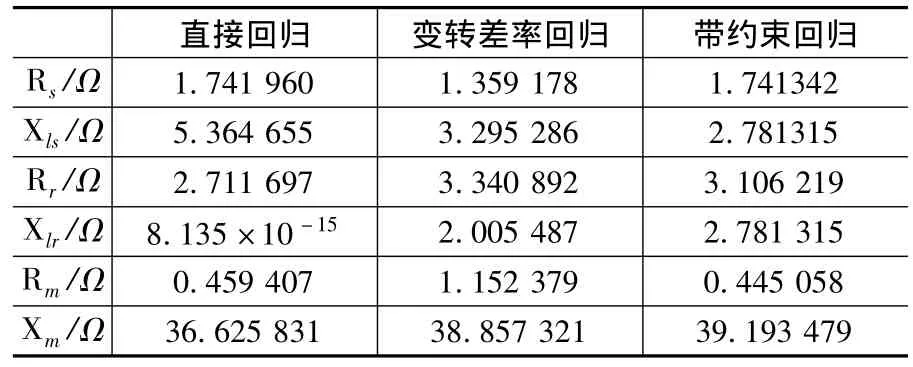
表7 3種回歸方式的結果比較
4 驗 證
已知樣機YLEWF-6三相異步力矩電機的冷狀態下直流電阻測量值如表8所示。
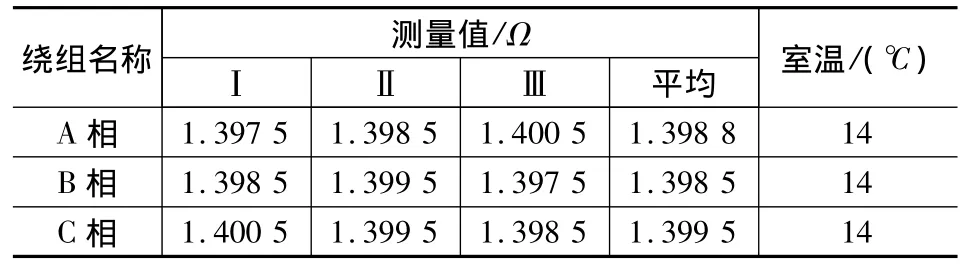
表8 直流電阻測量結果匯總
將定子繞阻平均相電阻值換算到標準工作溫度75℃下:
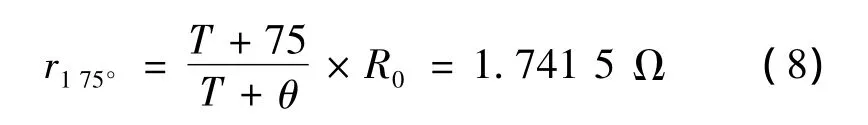
式中:對于銅導線T=225。
定子繞組的電阻除了與溫度有關外還與所通入的電流頻率有關。由于集膚效應的影響,同一繞組交流電阻值要稍大于直流電阻值。因此實際負載時的定子繞組的電阻值在式(8)的附近變化。假定變化范圍為±10%,則有:
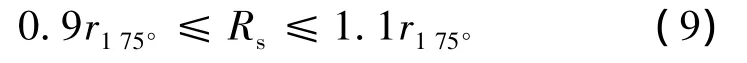
代入數值得:
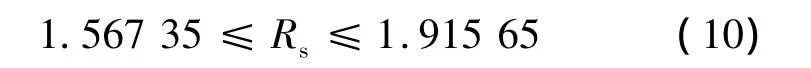
由式(10)可以看出,第3種的擬合方法得出的定子電阻值最合理。其它參數的大小比例關系也符合力矩電機的實際物理情況,當然其它的數據的準確性還需進一步的驗證。
也可以將式(10)作為約束條件放在回歸模型中,從而得到更準確的參數值。
5 結 語
在忽略機械損耗的基礎上,推導了異步電動機等值電路的參數回歸模型,并由回歸模型利用1stopt,探討了可以快速簡潔求出比傳統方法更為準確的數值解的原理,并對幾種參數回歸方法進行了有益的嘗試。文中回歸的結果表明,忽略機械損耗的參數回歸模型的回歸結果不夠理想,因此應該將機械損耗也作為一個待回歸的參數加入到回歸模型中,但這需要更大量的計算,要有好的算法或軟件支撐。
實驗數據處理的準確程度也有賴于數據測取的數量和精度,回歸方法是在大量的觀測數據中尋找變量之間內在的聯系,因此文中所提出的三種擬合對電機對參數更準確測定有一定的應用價值和指導意義。在此基礎上,可以進一步研究加權擬合/回歸等算法以及變換改進回歸模型來取得更好的擬合/回歸效果,當然數據越多擬合的精度越高,也越符合異步電動機實際的等值電路參數值。
盡管是針對于異步電動機的參數測定的數據處理,但參數回歸的方法也可以推廣到變壓器和其它類型的電機參數測定的數據處理中。
[1]Fitzgerald A E,Charles Kingsley,Jr.,Stephen D Umans.電機學(第6版)[M].劉新正,蘇少平,高林,等譯.北京:電子工業出版社,2004.
[2]林友杰,吳漢光.異步電機等值電路參數計算的一種新方法[J].福州大學學報(自然科學版).2006,34(4):512-515.
[3]馮浩,金陽,鐘德剛,等.異步電動機等值電路參數高精度計算方法探討[J].電機與控制應用,2001,28(3):1-6.
[4]董改花.三相異步電動機等值電路參數計算的綜述[J].煤礦機械,2006,27(2):207-2010.
[5]尹文怡,范通讓.電動機試驗數據擬合算法的研究與實現[J].微電機,2009,42(3):93-95.
[6]李建軍,盛潔波.異步電機定轉子參數的辨識方法研究[J].電工技術學報,2006,21(1):70-74.
[7]張微,王長江.一種新型感應電機的參數自測定方法[J].大電機技術,2003(1):18-23.
[8]武建文,李德成.電機現代測試技術[M].北京:機械工業出版社,2010.
[9]七維高科有限公司.1stopt 3.0用戶手冊[M].2009.

