基于CEI的飛船交會對接遠程導引段的軌道確定方案*

李曉杰，杜 蘭，黃 金

(1.解放軍信息工程大學測繪學院，河南 鄭州 450052;2.61768部隊，海南 三亞 572400)

我國的載人航天事業正處于飛速發展階段，到目前為止，神州飛船系列已進行4次無人發射、3次載人發射，并全部取得成功。運輸飛船與目標飛行器的交會對接、建立空間實驗室將是我國航天領域下一階段要實現的目標。為實現這些目標，有眾多的技術難題需要解決。其中交會對接的遠距離導引及近距離第一次導引的實時高精度測定軌就是急需解決的問題之一［1］。針對飛船的交會對接，傳統方法為射電波段的測距測速或者采用GPS進行相對導航，基本可以滿足其精度指標。但隨著航天任務的增多，傳統測控系統負荷量的增大，有必要尋求新的高精度測定軌技術來增強和補充我國的測控技術。

相位干涉測量是一種基于飛行器下行信號的被動測角跟蹤方法，其中中短基線相位干涉測量(CEI)具有基線短、精度高、實時性好等特點［2－4］，非常適用于對同步軌道及其以內地球衛星的現有測控手段進行增強和補充。本文探討了CEI技術在飛船交會對接遠程導引段的精密軌道確定及實時軌道監控的能力，以考察其作為備份技術的可行性。

1 空間交會對接各階段的精度要求

空間交會對接包含兩部分相互銜接的空間操作:空間交會和空間對接，簡稱RVD［5］。航天器的空間交會對接可以劃分為遠距離導引段、近距離導引段、停靠和對接段。各階段的情況介紹見表1。

表1 各階段對測量精度的要求與當前測量設備Table 1 Requirement for the measurement precisions in different phases and current measurement equipments

2 軌道仿真方案確定

低軌衛星過境的時間較短(每圈我國境內測控站可觀測時間為幾分鐘)，為了獲取盡可能多的觀測數據，在遠程導引段(兩個航天器不在天線的同一個波束內)，在測控站設置兩套CEI干涉系統，分別對每個航天器進行追蹤測量。把測量的數據送到同一個數據處理中心，進行采集、相關處理、數據融合，得到兩個航天器的相對位置和相對軌道。由于兩套系統位于同一測站，數據傳輸延遲可以忽略，實時性很好。

2.1 精密軌道確定的仿真方案

為更真實地反映各誤差源對定軌結果的影響，可采用統計的方法［6］。采用外符合精度進行精度評定。仿真流程如下:

(1)首先模擬一條真實軌道，并根據觀測方程模擬含有隨機噪聲和系統噪聲的觀測數據文件(本文假設初始模糊度之差已知);

(2)根據先驗軌道的誤差，采用批處理的方法解算初始時刻的軌道［7］;

(3)重新產生隨機噪聲，再進行軌道解算。

利用40組觀測數據文件的解算結果進行統計分析。在每個觀測及外推時刻分別比較“真實軌道”和解算出的軌道在徑向(R)、沿跡向(T)、法向(N)(該時刻真實軌道的R、T、N方向)上的位置或速度誤差得到Δi，最后利用(1)式得到位置或速度三分量的誤差RMS(σ)，再由三分量誤差計算得到總的位置或速度精度。

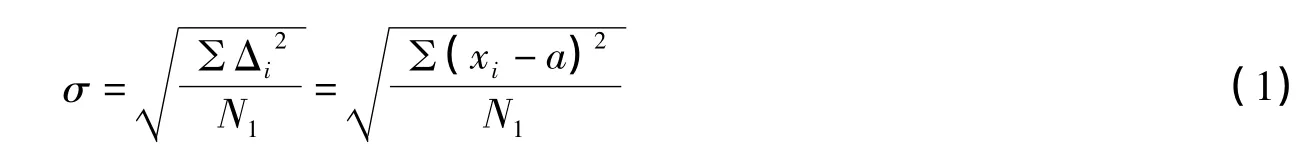
其中{xi}，i=1，…，N1為由歷元的定軌結果進行軌道外推的一列軌道量，a為由歷元的“真實軌道”進行軌道外推值。相對定軌精度:兩個航天器的絕對軌道各分量的解算值作差即為相對軌道各分量的解算值，而兩個航天器的絕對軌道各分量的真實值作差即為相對軌道各分量的真實值，每個觀測時刻及外推時刻的相對軌道各分量的解算值和真實值作差即為此時刻各分量的相對軌道誤差，仍以(1)式得到此次定軌的相對軌道精度。

2.2 實時軌道監控的仿真方案

采用單一絕對濾波器方案進行定軌［8－9］。

采用擴展卡爾曼濾波器同時求解兩個航天器的絕對位置、速度，而后做差求取相對位置、相對速度。在具體實施中，由于解算只在其中一個航天器中進行，所以航天器可以只有一個，實現較為方便。由于兩航天器不是同時進入測控站的可測控范圍內，故每個航天器獨自進行實時的絕對位置計算，在兩個航天器均有觀測數據時才能進行相對軌道計算，當一個航天器還有觀測數據而另一個沒有觀測數據時就用動力學特性進行軌道外推來獲得其絕對軌道。

仿真程序由系統模擬和EKF導航濾波器兩部分組成。系統模擬輸出模擬測量數據，測量數據輸入到導航濾波器，濾波器據此對預測的軌道進行修正并給出估計軌道。

濾波精度的定義:濾波器收斂后的每一時刻的軌道誤差的均方差。位置、速度六分量的誤差RMS(σ)。

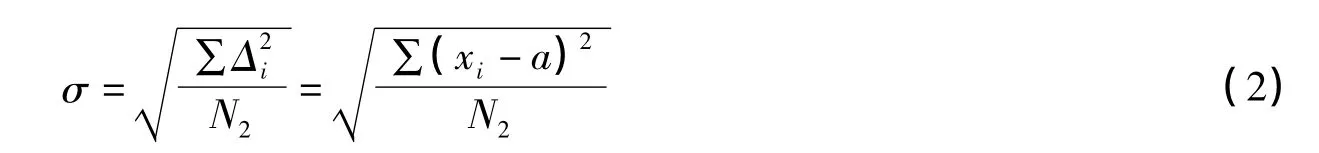
其中{xi}，i=1，…，N2為由濾波器得到的一列軌道量，a為由同一歷元的“真實軌道”的軌道外推值，將計算出的標準誤差σ作為此次絕對軌道精度。有了每個航天器的每一時刻的絕對軌道誤差，即可參照2.1中的方法得到相對軌道精度。

3 仿真條件

(1)衛星的初始時刻軌道選取:初始歷元時刻為UTC2008-7-122∶35∶00，該時刻兩顆低軌衛星(sat1、sat2)的軌道數據由 STK 生成［10］(見表2)。

表2 LEO初始時刻的軌道根數Table2 Orbital roots of two LEO satellites at initial moments

兩小時內兩衛星過境兩次，相對距離在90～20.05 km之間變化。

(2)采用相位延遲率觀測量進行精密軌道確定，非差相位延遲觀測量進行實時軌道監控。以相位延遲率為觀測量時，觀測噪聲水平均取0.1 mm/s，系統偏差為1 mm/s。以非差相位延遲為觀測量時，觀測噪聲為1 cm，系統偏差取為常值參數10 cm。

(3)力學模型選取:動力學模型中采用JGM-3的20×20階重力場、日月引力攝動、大氣阻力攝動和光壓攝動力模型。先驗軌道位置誤差150 m，速度誤差0.5 m/s。采樣間隔為1 s。

(4)測控站布設:單基線組為V型布設的連線正交雙基線測控單元，每條基線長10 km。精密定軌時單基線組分別布設在上海、昆明、三亞，實時軌道監控只采用三亞站的數據。測站的高度截止角設為5°。上海站的雙正交基線單元為基線1、2，昆明站的雙基線為基線3、4，三亞站的雙基線為基線5、6。分別計算了衛星一次、兩次過境時各站與衛星間的可視弧段(要求同時可視兩顆衛星)，見圖1、2。

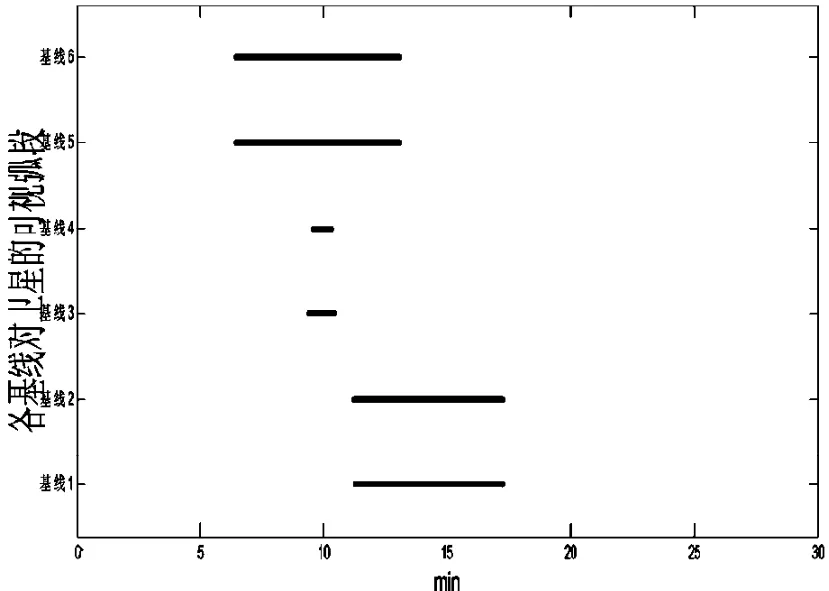
圖1 0.5小時內各站與衛星間的可視弧段Fig.1 Visible arcs of stations appearing to the two satellites within0.5 h

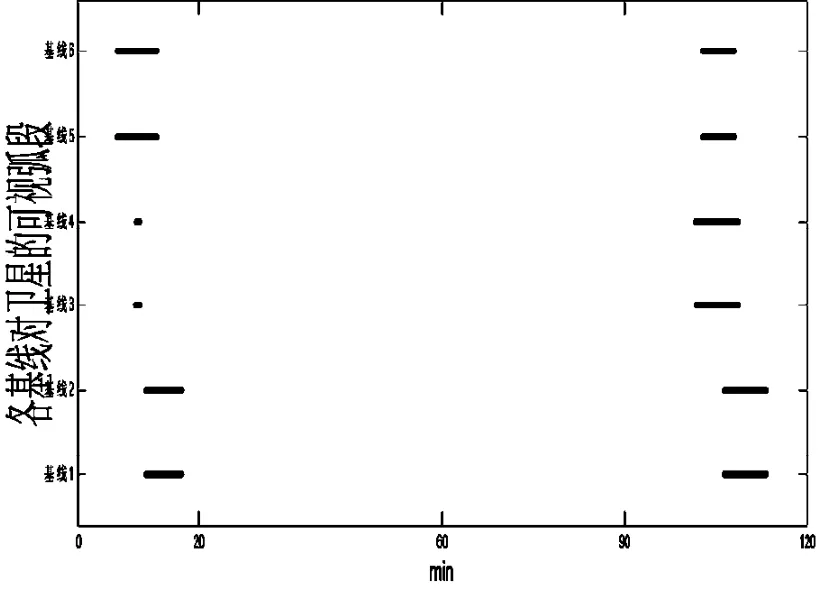
圖2 2小時內各站與衛星間的可視弧段Fig.2 Visible arcs of stations appearing to the two satellites within2 h

衛星一次過境，可觀測弧長的情況分別如下:昆明站為1 min，上海站為6 min，三亞站為6 min 40 s。衛星兩次過境，可觀測弧長的情況分別如下:昆明站為8 min，上海站為13 min，三亞站為12 min。

4 仿真結果分析

4.1 精密軌道確定的結果

估計參數為衛星狀態參數和大氣、光壓參數以及各基線上常值系統誤差。

采用衛星一次、兩次過境的數據得到各衛星的絕對及相對定軌精度，見表3、4、5，位置分量精度單位為m，速度分量精度單位為m/s。

表3 衛星1的絕對定軌精度Table 3 Absolute accuracy of orbit determination for satellite 1

表4 衛星2的絕對定軌精度Table 4 Absolute accuracy of orbit determination for satellite2

表5 兩衛星間的相對定軌精度Table 5 Relative accuracy of orbit determination between the two satellites

(1)無論是絕對定軌精度還是相對定軌精度，其對弧長均很敏感。參與定軌的測控站越多，定軌精度越高。

對三亞和上海來說，比較衛星一次過境與兩次過境的定軌結果，約兩倍的觀測數據量使得衛星的絕對定軌精度(位置)由一百多米提高到米級，速度分量由分米/秒級提高到厘米/秒級甚至毫米/秒級，相對定軌精度(位置)由幾十米級提高到米級，速度分量由厘米/秒級提高到毫米/秒級。

雙站利用衛星一次過境時的數據可使絕對位置精度達幾十米，速度精度達分米/秒級，相對位置精度達米級，速度達厘米/秒級;利用兩次過境時的數據可使絕對、相對位置精度達分米級，速度精度達毫米/秒級。

三站利用衛星一次過境時的數據可使絕對定軌精度(位置)達米級，速度達毫米/秒級，相對位置精度達分米級，速度達毫米/秒級。

(2)由于在遠程導引段相對軌道精度要求較低，優于100 m即可。除了昆明采用衛星一次過境時的數據的情況以外，別的情況均能滿足其要求，此時速度精度可達0.12 m/s以內。

4.2 實時軌道監控的結果

固定模糊度參數的卡爾曼濾波算法，分為兩個過程:

(1)將模糊度參數作為濾波狀態向量的一部分，與航天器的狀態量一起求解。在濾波充分多步后，可獲得與真實的模糊度接近的模糊度初值;

(2)固定整周模糊度，只需求解航天器的狀態量，以此再進行高精度的相對定軌。采用衛星一次過境的數據得目標航天器和追蹤航天器的濾波精度見表6、7。

表6 目標航天器的濾波精度Table 6 Filtering accuracy for a target spacecraft

表7 追蹤航天器的濾波精度Table 7 Filtering accuracy in tracking a spacecraft

采用非差分CEI作為觀測量對單航天器進行EKF濾波，絕對位置精度可達十米級，速度精度可達厘米/秒級。

圖3、4是整周模糊度的濾波結果。圖5～10是目標航天器的絕對位置和絕對速度濾波結果。

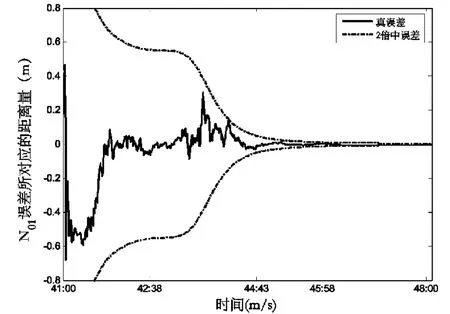
圖3 N01的濾波結果Fig.3 Filtering result of N01

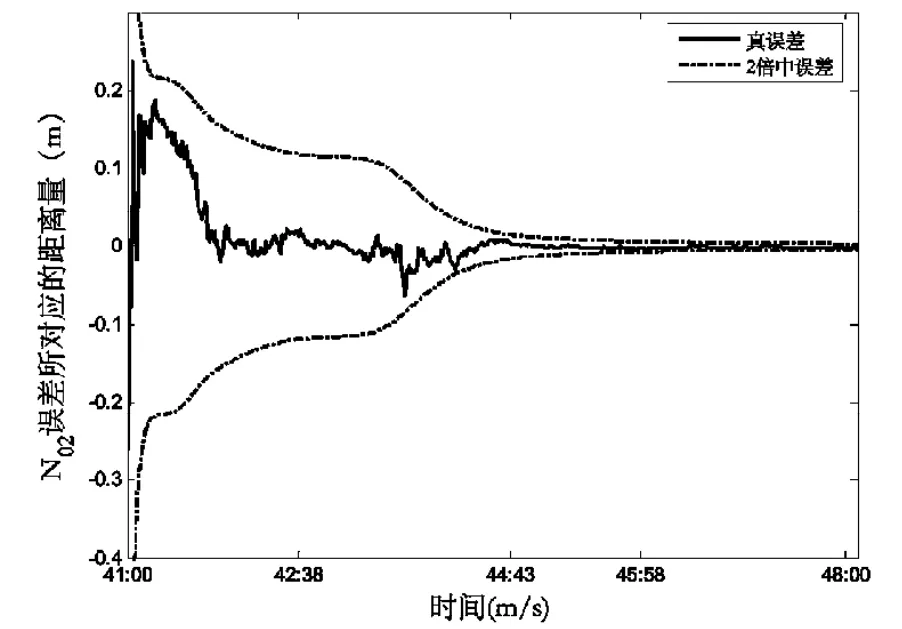
圖4 N02的濾波結果Fig.4 Filtering result of N02

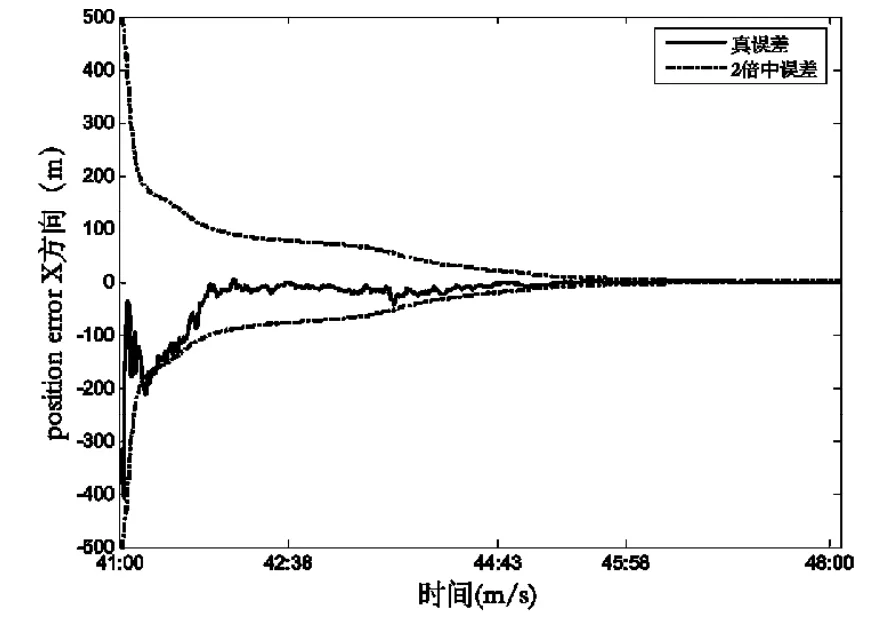
圖5 目標航天器位置X方向的濾波結果Fig.5 Filtering result of X coordinate component of a target spacecraft

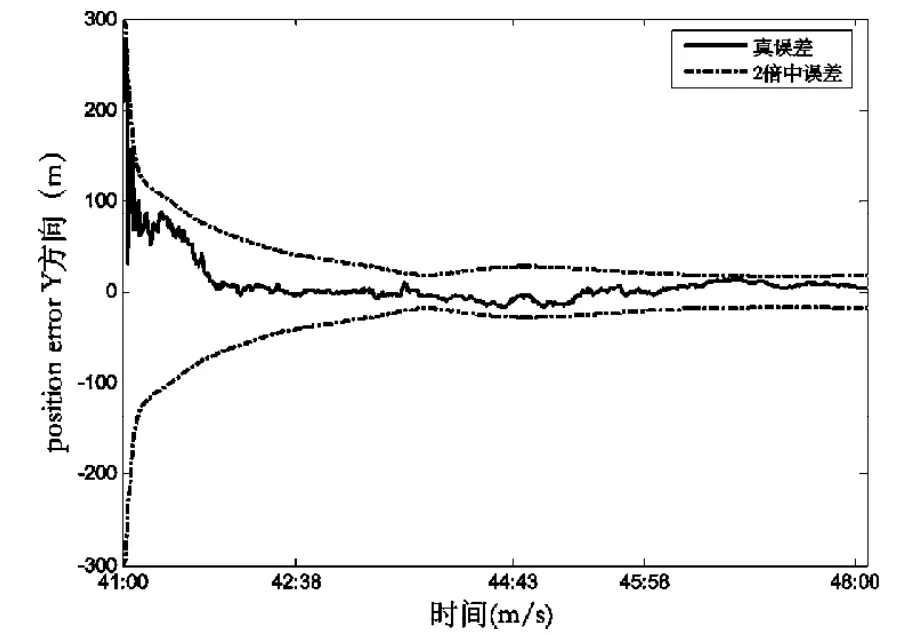
圖6 目標航天器位置Y方向的濾波結果Fig.6 Filtering result of Y coordinate component of a target spacecraft

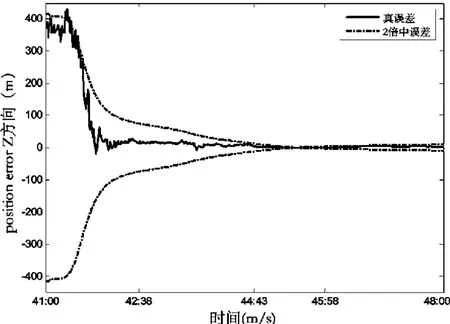
圖7 目標航天器位置Z方向的濾波結果Fig.7 Filtering result of Z coordinate component of a target spacecraft

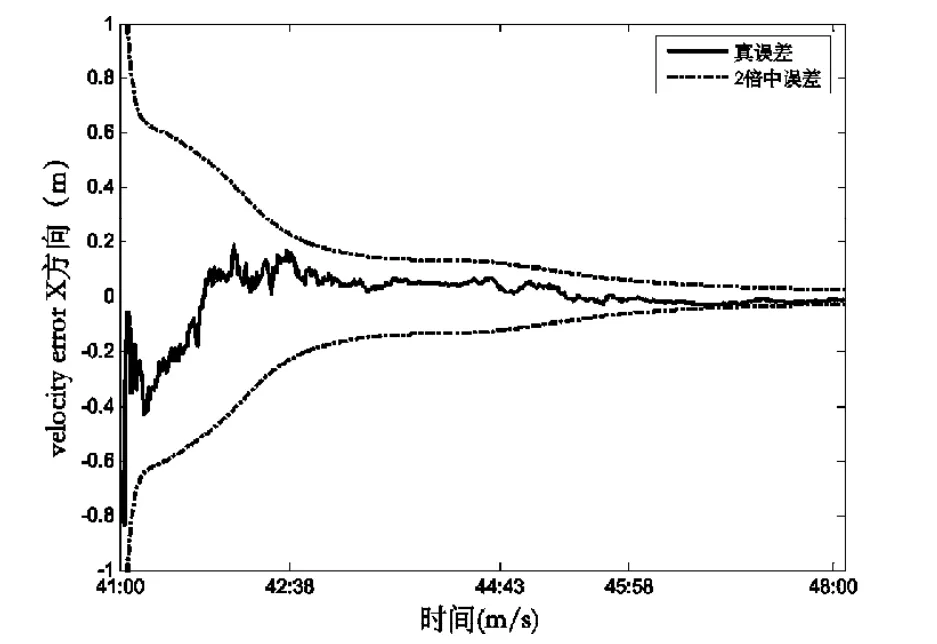
圖8 目標航天器速度X方向的濾波結果Fig.8 Filtering result of X velocity component of a target spacecraft

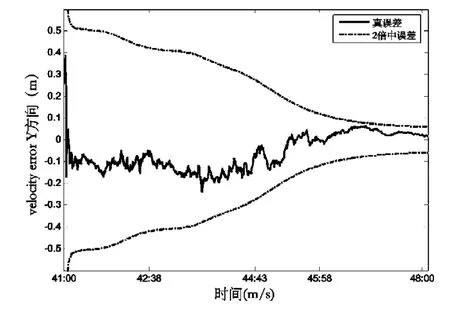
圖9 目標航天器速度Y方向的濾波結果Fig.9 Filtering result of Y velocity component of a target spacecraft

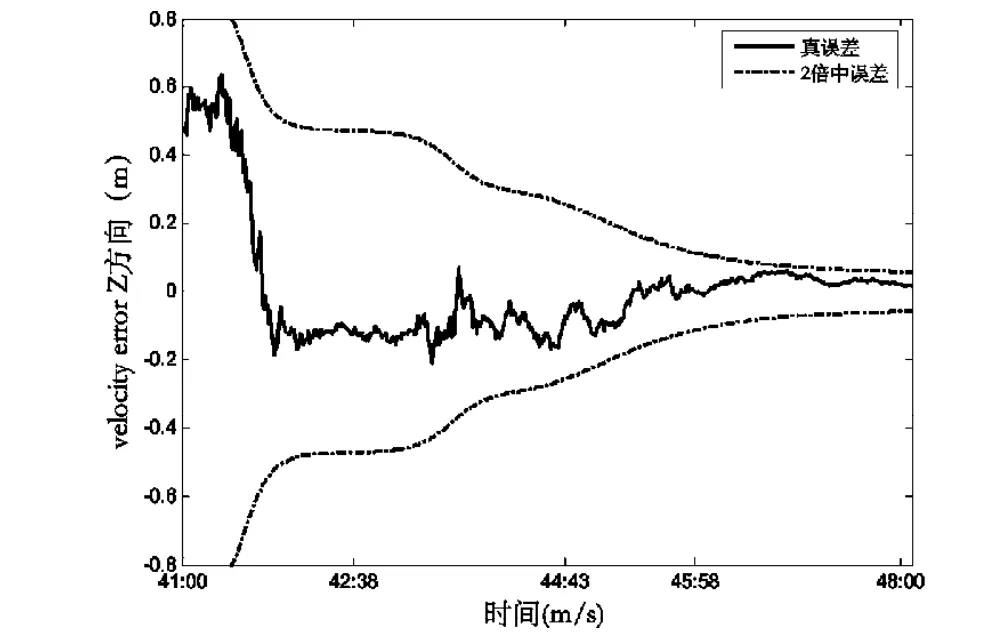
圖10 目標航天器速度Z方向的濾波結果Fig.10 Filtering result of Z velocity component of a target spacecraft

以上各圖中實線代表軌道各分量的真誤差，虛線代表軌道各分量的2倍中誤差。由以上各圖可以看出正負2倍的中誤差可以包絡真誤差。由圖3～10可知N0需要4 min可以收斂，此時固定N0，位置三分量和速度三分量則需要大約5 min可以收斂。

相對軌道精度見表8。

表8 相對軌道精度Table 8 Relative accuracy of orbit determination

由表8可知，相對軌道精度略差于絕對軌道精度。分析原因，可能是因為目標航天器的初始軌道誤差對其產生了較大的影響。

5 結論

在飛船交會對接的遠程導引段，地基測軌精度需要有一個大的提升。CEI非常適用于對同步軌道及其以內地球衛星的現有測控手段進行增強和補充。因此本文探討了CEI技術在飛船交會對接遠程導引段的精密軌道確定及實時軌道監控的能力，仿真結果如下:

(1)精密定軌中，采用可視弧段較長的單站即可使得絕對定軌精度達一百多米，速度精度達分米/秒級，相對軌道精度在百米以內，速度精度達由厘米/秒級，如文中的三亞、上海站。雙站可使絕對位置精度達幾十米，速度精度達分米/秒級，相對位置精度達米級，速度達厘米/秒級;三站可使絕對定軌精度達米級，速度精度達毫米/秒級，相對位置精度達分米級，速度達毫米/秒級。均能滿足遠程導引段的精度指標。

(2)實時軌道監控時，使用單一絕對濾波器的方案可使相對軌道位置精度可達十米級，速度精度可達厘米/秒級，滿足遠程導引段的精度指標。

［1］Catherine L Thornton，James S Border.Radiometric Tracking Techniques for Deep Space Navigation ［J］.Jet Propultion Labrotary California Institude of Technology，2000，11(10):3－7.

［2］C D Edwards.Short Baseline Phase Delay Interferometry ［A］.TDA Progress Report，1987:46－56.

［3］S Kawase，F Sawada.Interferometric Tracking for Close Geosynchronous Satellites ［J］.The Journal of the Astronautical Sciences，1999，47(1－2):87－97.

［4］C D Edwards.Goldstone Intracomplex Connected Element Interferometry ［J］.TDA Progress Report，1990:1 －12.

［5］林來興.空同交會對接技術 ［M］.國舫工業出版社，1995:75－78.

［6］李曉杰，杜蘭，黃金，等.對單組短基線相位干涉測量的GEO定軌精度的改進方法研究［A］，2008年航天器測控技術研討會，2008.

［7］李濟生.人造衛星精密軌道確定 ［M］.北京:解放軍出版社，1995:80－90.

［8］韓令軍，楊麗，孫冬梅.基于EKF算法的單站無源定位研究 ［J］.電信交換，2008，(1):22－27.Han Lingjun，Yang Li，Sun Dongmei.Study of Single-satation Passive Positioning by EFK［J］.Telecon Communication，2008，(1):22 －27.

［9］劉廣軍、吳曉平、田慶新.GPS用于航天器交會對接的方案與模糊度OTP解算研究［J］.航天空制，2001，3:6－11.Liu Guangjun，Wu Xiaoping，Tian qingxin.Scenarios of Applying GPS for Spacecraft RVD and the Study of Applying OTP Ambiguity-resolation Method ［J］.Spaceflight Contron，2001，3:6－11.

［10］楊穎、王琦.STK在計算機仿真中的應用 ［M］.北京:國防工業出版社，2005.01.