基于腦部CT圖像的LOG算子改進

朱丙麗

（重慶三峽學院計算機科學與工程學院，重慶萬州 404100）

1 腦部CT圖像的邊緣特征

從本質上講，邊緣是數字圖像中具有灰度級躍變性質的像素點，邊緣是一個區域的開始，也是一個區域的結束，一條邊緣是一組相連的像素集合.理想情況下，邊緣點的灰度級躍變是垂直線條式的躍變模型，寬度為1像素.而實際上，由于受到各種因素的影響，邊緣處的灰度變化如附圖1所示，[1-2]邊緣是由灰度值開始躍變到變化基本終止之間的像素構成，落在斜坡上的像素決定了邊緣的寬度.

實踐中，由于圖像采集系統的不完善、取樣率不高、照明條件不好、設備的噪聲等因素使得邊緣具有模糊性，這種模糊程度決定了附圖1中的斜坡線段的長度.分析中，不僅要考慮邊緣灰度變化的幅度，而且要考慮邊緣的方向.若在XY平面直角坐標系上，腦部CT圖像的頭骨邊緣呈弧形，整個形狀類似橢圓，對于左右兩側的邊緣，X軸方向上的灰度級躍變最大；對于上下兩側的邊緣，Y軸方向的灰度級躍變最大.

2 LOG算子

LOG算子分兩步實現，[3-7]第一步用高斯函數處理圖像，對去除常見于CT圖像中的正態分布噪聲很有效，標準偏差σ影響邊緣的模糊程度；第二步用拉普拉斯算子檢測邊緣，它是對于二元函數的二階導數算子，對應的過零點就是邊緣位置，算子強調圖像灰度的突變，能增強細節信息，有銳化效果.經過數學運算，LOG作用于像素值的公式見（1），理想情況下，▽2（x，y）近似的5×5模板稱為LOG算子模板，根據處理對象的特征，可對其進行改進.

3 傳統LOG算子邊緣分割結果與分析

附圖2是一張腦部CT的原始圖像及對應的傳統LOG算子分割結果.我們可以做如下分析：[3-7]

（1）LOG算子在使用高斯函數抑制噪聲的同時也將原有的比較尖銳的邊緣平滑掉，造成一些尖銳邊緣無法檢測到.（2）高斯函數的參數σ對不同頻率噪聲的抑制作用不同，會造成邊緣信息丟失、虛假邊緣的產生.（3）拉普拉斯算子對圖像中的階躍型邊緣點定位準確，但是對噪聲非常敏感，抗噪聲能力比較差，使用拉普拉斯算子會使噪聲成分得到加強；同時該算子是無方向的量，容易丟失部分邊緣的方向信息，造成一些不連續的邊緣檢測.（4）對LOG算子計算時，模板的近似構造很重要，運算中，默認模板的使用會在一定程度上影響圖像分割效果.

4 LOG算子的改進

對腦部CT圖像進行邊緣分割時，要突出頭骨邊緣的細節，但由于圖像灰度的動態范圍很窄、圖像較暗且有很高的噪聲，單獨使用一種操作方法很難達到理想的分割效果.改進方法要在噪聲抑制，細節增強、體現邊緣灰度特征方面尋求平衡點，綜上所述，改進算子的偽代碼是：[5-10]

（1）讀取圖像f，并作double類型轉換.（2）使用 LOG算子模板對原始圖像進行濾波，得到圖像gb.增強頭骨邊緣的細節，有銳化效果但是也增加了噪聲.選用什么模板要根據圖像的特點及變化函數來確定.此外，經過實驗對比，使用LOG算子模板效果最好.（3）用原圖像與上步獲得的圖像相加進一步銳化圖像得到更多的細節，生成圖像gc.（4）前兩步操作增加了圖像的噪聲，接下來計算梯度幅度值進行線性濾波消除噪聲，得到圖像gd.令hv=[-1 -2 -1;0 0 0;1 2 1]，求轉置hh=hv.'，分別用hh、hv對圖像進行濾波后取絕對值得到gv、gh，再用sqrt(gv.^2+gh.^2)計算像素的梯度值.使用該濾波器，在邊緣方向和變化幅度上均有考慮.（5）用二維中值濾波函數medfilt2降低CT圖像中常見的椒鹽噪聲，生成圖像ge.（6）用LOG算子進行邊緣分割，得到圖像g.（7）對圖像進行二值化處理，得到圖像g.（8）輸出圖像g.

5 改進LOG算子的實驗結果及分析

實驗工具使用MATLAB 7.5，[11-12]安裝占用的硬盤空間至少 3.25GB，運行占用內存空間至少120MB；軟硬件環境是普通PC機、Windows XP操作系統.改進方法中，令平滑因子σ、邊緣灰度閾值T、medfilt2的m×n鄰域值取恰當的值，會靈活的得到下面的分割結果.其中m×n＝3×3，σ＝2是默認取值.

附圖3展示了σ值對邊緣線條的影響程度，σ值越小，模糊程度越低，線條的細節展示得越細致；σ值越大，模糊程度越高，線條展示得越粗略，邊緣線條出現間斷、缺省情況；σ值明顯的影響了整張圖像上微小的、主要的或說各種灰度突變處的線條生成.

附圖4展示了邊緣灰度閾值T的作用.顯示時，比T小的像素被忽略，大于或等于T的像素生成邊緣線條；T的取值并不是在整個灰度區間[0，255]都是有效的，根據實驗用的腦部CT圖像，T的取值在區間[0.3，3]上具有分割價值；算法自動選取的值是 T＝0.8311，可以根據應用需求在此值附近及有效區間上進行調整，以滿足分割需求.

附圖5展示了二維中值濾波函數medfilt2鄰域m×n的大小對邊緣分割效果的影響.鄰域越小，保留的細節越多，生成的邊緣線條更細致、連續；鄰域越大，濾除的細節越多，生成的邊緣線條更粗略，甚至在主要的灰度突變處出現邊緣不連續情況.

根據被處理圖像的特征，應用本改進算子，選取恰當的參數，能靈活的得到各種有價值的邊緣分割圖，能滿足不同的分割需求.

6 運算時間對比與分析

在100張腦部CT圖像的實驗中，挑選了5張代表性的圖像運算做了統計，見圖6，可以看出：改進LOG算子與傳統LOG算子的運算速度根據不同的圖像會有輕微的變化，但是從線條表現出的平穩程度來看運算效率均比較穩定，其中傳統方法更加穩定，這是改進算法需要提升的地方；改進LOG算子比傳統LOG算子對圖像的處理耗時要多，但是仍然在可以接受的秒級范圍內，這是改進算法需要提升的地方.

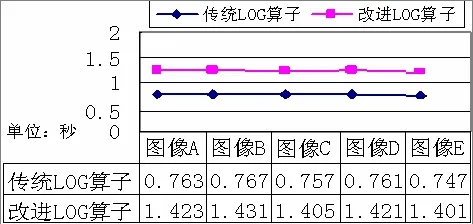
圖6 傳統及改進LOG算子的運算時間對比圖

實驗中，算法運行對硬件和軟件環境要求高，依賴度也高，在不同的環境下運行的時間有較明顯的差別；圖像對不同的濾波操作很敏感，尤其是一些組合性的操作步驟，常常會顧此失彼，這需要反復試驗，在不同的因素間達到平衡.對于運算時間，主要耗費在于對圖像矩陣中像素的處理，空間耗費類似.目前在應用中，計算機的內存趨向于大容量，處理時間與效率的協調顯得更重要，甚至在某些情況下，通過消耗更多的空間來獲取時間上的高效率和分割結果上的高質量.

附 圖：

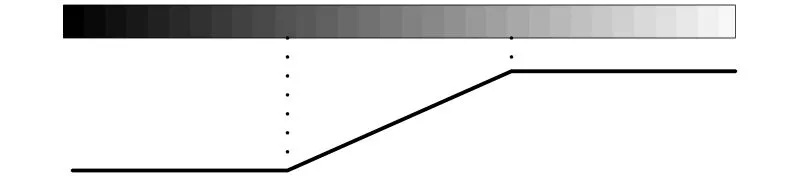
附圖1 邊緣灰度變化模型

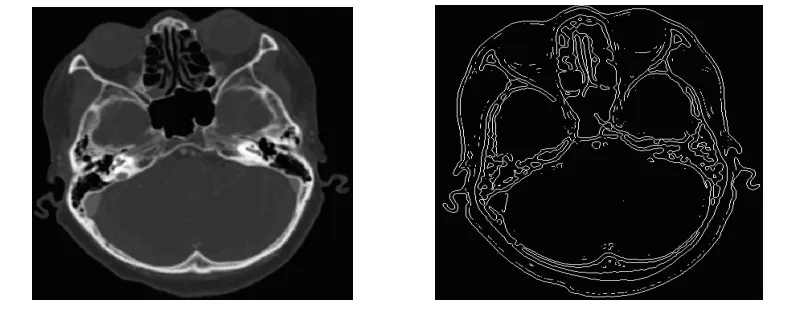
附圖2 原圖及傳統LOG算子邊緣分割結果

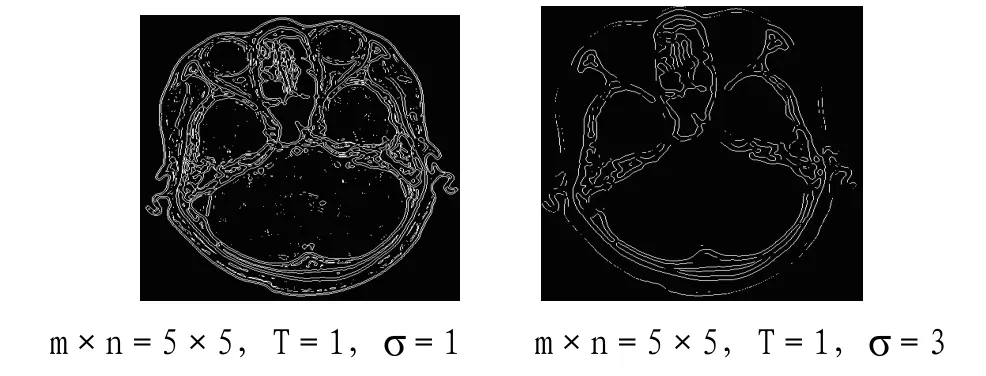
附圖3 σ值對分割結果的影響

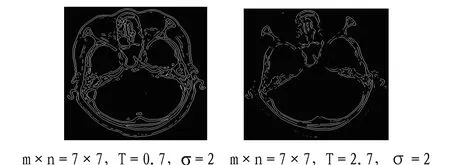
附圖4 T對分割結果的影響

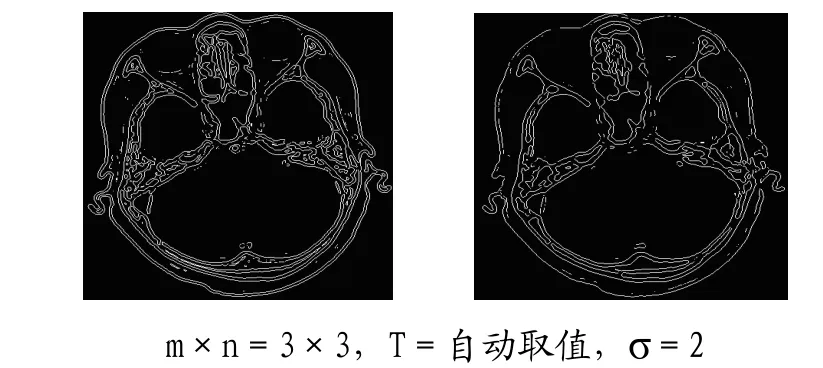
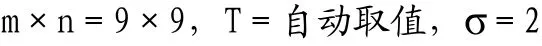
附圖5 m×n對分割結果的影響

[1]Rafael C. Gonzalez，Richard E. Woods，Steven L. Eddins.數字圖像處理（第二版）[M].阮秋琦，等譯.北京：電子工業出版社，2009.

[2]姚敏.數字圖像處理[M].北京：機械工業出版社，2006.

[3]Chu, C. -C, and Aggarwal, J. K. The Intergration of Image Segmentation Maps Using Regions and Edge Information[J].IEEE Trans. Pattern Anal.Machine Intell.1993(12).

[4]Marr, D., and Hildreth, E. Theory of Edge Detection[J]. Proc. R. Soc. Lnd., 1980(B207).

[5]Canny, J. A Computation Approach for Edge Detection[J].IEEE Trans, Pattern Anal Machine Intell.1986(6).

[6]Clark, J. J. Authentication Edges Produced by Zero-crossing Crossing Algorithms[J].IEEE Trans. Pattern Anal. Machine Intell.1989(8).

[7]Gunn, S. R. Edge Detection Error in the Discrete Laplacian of a Gaussian, Proc[C].1998 Int’l Conference on Image Processing (II), 1998.

[8]程廣斌.應用于數字化診斷的若干醫學圖像分析方法研究[D].南方醫科大學，2008.

[9]何培培.腦部 CT圖像處理研究[D].長沙理工大學，2008.

[10]張太發，程東旭，石瑞銀.基于Log算子的一種新的邊界輪廓線提取方法[J].計算機工程與應用，2008（22）.

[11]Rafael C. Gonzalez，Richard E. Woods. 數字圖像處理（MATLAB版）[M].阮秋琦，阮宇智，等譯.北京：電子工業出版社，2009.

[12]MATLAB 官 方 網 站 .Documentation[OL]. http://www.mathworks.com/，2009.