轉爐減速器齒輪瞬態本體溫度場分析

林建筑（天津天鋼聯合特鋼有限公司，天津 301500）

轉爐減速器齒輪瞬態本體溫度場分析

林建筑（天津天鋼聯合特鋼有限公司，天津 301500）

針對轉爐減速器齒輪承載越來越高的現狀，利用齒輪嚙合理論、摩擦學、傳熱學、赫茲接觸等理論，研究了齒輪的相對滑動速度及輪齒摩擦系數的變化規律，計算出了齒輪沿嚙合線摩擦熱流量。通過建立轉爐減速器齒輪瞬態溫度場有限元分析模型，獲得了齒輪瞬態本體溫度場，齒輪工作時間與溫度梯度的關系表明越是能迅速達到熱平衡狀態，對轉爐減速器齒輪傳動越有利。該研究結果為轉爐減速器齒輪的安全使用提供了理論依據，為以后轉爐減速器齒輪瞬態本體溫度場的快速建模和分析提供了方法。

轉爐 減速器 齒輪 傳動 瞬態溫度場 有限元 膠合承載能力

1 引言

根據《鋼鐵產業調整與振興規劃》強制標準，2011年底前淘汰了30 t及以下煉鋼轉爐、電爐，強化行業準入管理，嚴控高耗能、高污染企業盲目發展。隨著轉爐的不斷擴容，要求轉爐減速器齒輪具有可靠性高、扭矩大、功率密度高等特點。同時，重載導致齒輪輪齒承受較高的熱負荷，過高的溫度不僅會引起輪齒熱變形，還會嚴重影響輪齒的潤滑效果和傳動性能。另外，齒面溫度過高也是引起膠合的主要因素之一，因此研究轉爐減速器齒輪瞬態溫度場具有十分重要的理論與現實意義。

齒輪的溫度場由2部分構成：齒面本身的本體溫度和輪面的瞬時溫度。對于齒輪本體溫度場，Martins R[1]利用有限元法估算了直齒圓柱齒輪本體溫度場，并對動載荷、油膜厚度進行了理論分析和數值計算。國內的龍慧、肖望強均采用該方法對定軸圓柱齒輪本體溫度進行估算[2-3]，并取得了較為滿意的結果。而對齒面的瞬時溫度研究，以往文獻主要采用BLOCK公式進行計算[4-6]，但該方法并不能確定輪齒溫度分布，而通過有限元法可以全面分析轉爐減速器工作齒面溫度分布情況。

本文以120 t轉爐減速器齒輪為研究對象，利用齒輪嚙合原理、齒面接觸應力分析、摩擦學和傳熱學理論，分析摩擦熱流密度的分布狀況，采用有限元法獲得齒輪瞬態溫度場，得到嚙合過程齒輪齒面瞬時溫度分布。

2 齒面摩擦熱流量計算

2.1 齒面相對滑動速度變化與分布

齒輪嚙合齒輪副的相對滑動導致了摩擦熱的生成，由齒面承受載荷、旋轉速度和齒面的摩擦系數而共同決定。因此，齒輪嚙合面產生的摩擦熱流量對輪齒溫度的分布以及熱平衡具有重要影響。

為了分析在一個嚙合循環中齒輪嚙合點切向速度的變化，引入無量綱參數Γ來表示任意嚙合點在嚙合線的位置，如圖1所示。

圖1 嚙合線無量綱坐標

式中：u為齒的數比；ry1為小齒輪上嚙合點半徑；αy1為小齒輪上嚙合點壓力角。

取理論嚙合線N1N2為坐標參考軸，嚙合線上任意一點y的無量綱坐標Γy為：

主動輪1、從動輪2的嚙合點沿接觸切線方向相對滑動速度vs為：

2.2 齒輪摩擦熱流量

每一個輪齒每旋轉一周均收到一次摩擦熱流量的輸入，因此，每一個旋轉周期大、小齒輪所獲得的平均摩擦熱流量可以分別表示為：

2.3 輪齒摩擦熱流量分析

選擇轉爐減速器齒輪傳動系統中的小齒輪作為對象，潤滑油初始溫度T1和空氣溫度T2為30，齒輪系統傳動功率P為75 kW，轉速n1為750 r/min，齒輪模數m為10 mm，主動齒輪1齒數為48，從動齒輪2齒數為144。

主動齒輪1的摩擦熱流量沿嚙合線的分布如圖2所示。橫坐標從左至右分別為雙齒齒根嚙入點、單齒嚙入點、嚙合節點、單齒嚙出點、雙齒齒頂嚙出點。

圖2 主動輪摩擦熱流量沿嚙合線的分布

由圖2可見，在接觸應力、相對滑動速度等綜合影響下，齒輪嚙合面摩擦熱流量的分布非常不均勻。就單齒嚙合區而言，其內接觸應力大，而相對滑動速度小，故摩擦熱流量很小；而在雙對齒嚙合區，盡管其接觸應力較小，但齒面相對滑動速度較大，因此摩擦熱流量要高于單齒嚙合區。

3 齒輪瞬態本體溫度場有限元分析

3.1 本體溫度熱平衡方程及邊界條件

齒輪在達到熱平衡狀態后，每一個輪齒都循環相同的加熱、傳熱周期，因此輪齒的熱平衡可以通過建立單個輪齒的模型來分析。

三維非穩態導熱微分方程一般形式為：

式中：ρ為密度；c為比熱容；λ為導熱系數；Ψ及t分別為單位時間內單位體積中內熱源的生成熱及溫度。

圖3為單個輪齒邊界條件示意圖，根據式（1）推導出，工作齒側A3的穩態導熱微分方程為：

式中：n為換熱表面外法向；h為邊界與周圍流體間表面傳熱系數；Tf為周圍流體溫度；q為邊界熱流密度值。

圖3 單個輪齒模型

對于非工作齒側A8，齒根面A2、A7，輪齒端面A5、A6，輪齒頂端外表面A4，穩態導熱微分方程為：

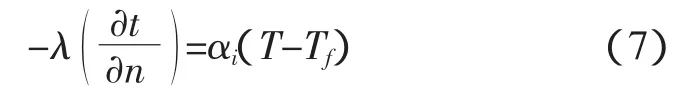
αi主要取決于齒輪的冷卻、潤滑方式及運行條件，本文根據輪齒熱網絡分析方法，由下式確定：

式中：Re為雷諾數；Pr為潤滑油普朗特數；K0為油導熱系數。

達到熱平衡狀態時，齒面摩擦熱是齒輪的主要熱源，并決定了輪齒穩態溫度場分布情況；而且在齒輪傳動過程中，工作齒側與潤滑油之間進行對流換熱，以避免溫升過高導致傳動效率降低及輪齒膠合，而熱量的傳輸狀況則取決于齒輪表面對流換熱系數。因此，在齒輪基本參數和材料性能確定的情況下，齒輪摩擦熱流密度及齒面對流換熱系數是決定齒輪本體溫度場的主要因素。

3.2 齒輪瞬態本體溫度場分析

根據給定參數，開發了轉爐減速器齒輪整體模型參數化程序，為了研究轉爐減速器齒輪在達到穩態之前的本體溫度場變化歷程，進行瞬態溫度場計算。

圖4為齒輪傳動系統開始運轉后經過5 min和20 min的輪齒瞬態溫度分布的計算結果。當運轉5 min時，轉爐減速器齒輪瞬態溫度場最高溫度達到穩定態最高溫度的80%左右；當運轉20 min時，該溫度場最高溫度可達穩態最高溫度的94%。由此可知，當轉爐減速器齒輪在運轉20 min時，可以認為齒輪傳動系統溫度場達到穩定狀態。

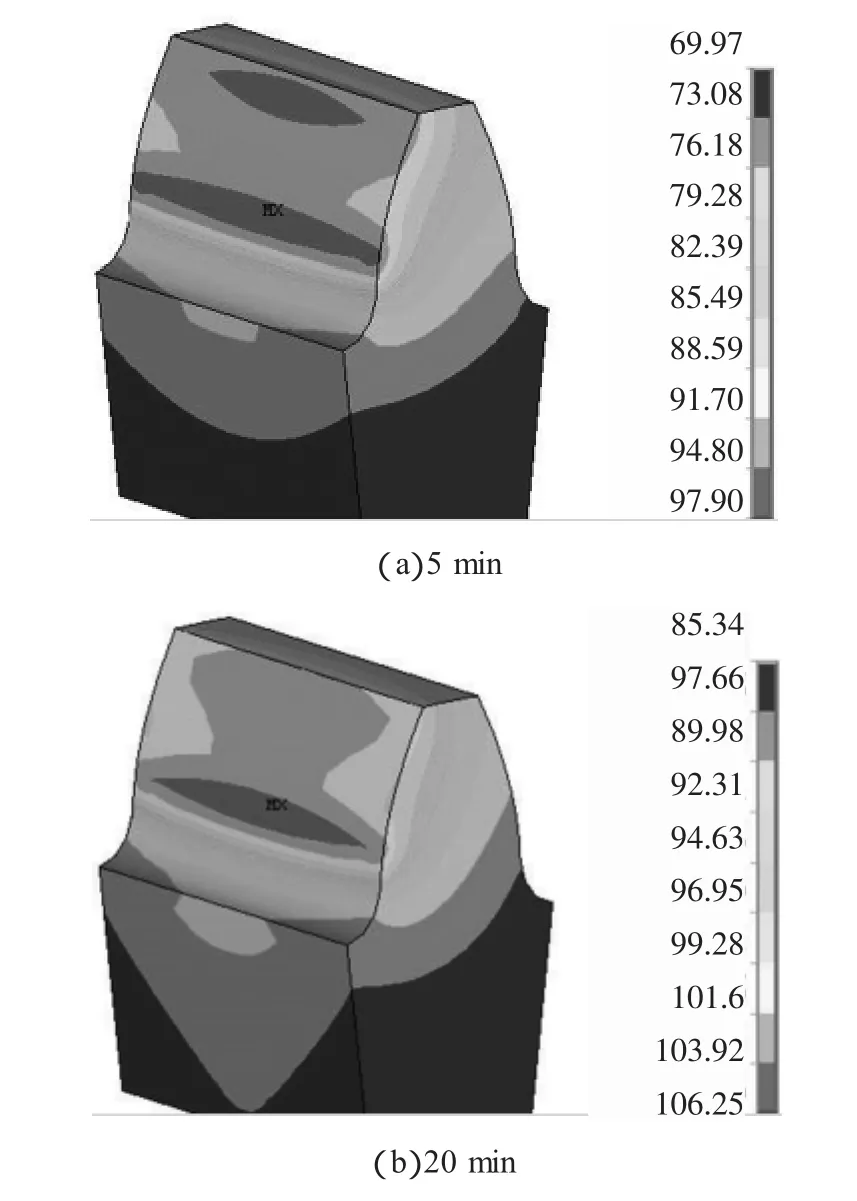
圖4 對稱齒輪瞬態本體溫度場

通過上述分析可以得出，在熱平衡狀態前，轉爐減速器輪齒瞬態溫度梯度大于熱穩定狀態，由于溫度梯度越大溫度分布就越不均勻，進而產生的附加熱應力越大，因此達到熱平衡狀態越快，對轉爐減速器齒輪傳動越有利。尤其當轉爐容量超過120 t，減速器齒輪傳動系統處于熱穩定狀態之前，瞬態溫度梯度較大，附加熱應力對齒輪傳動系統影響非常大。

4 結論

通過研究推導出了轉爐減速器輪齒滑動速度、摩擦熱流量等的計算方法，分析了這些參數沿輪齒嚙合線的分布形態，建立了轉爐減速器齒輪瞬態本體溫度分布模型，研究結果為轉爐減速器齒輪的安全使用提供了理論依據。在轉爐減速器輪齒溫度的分析方法、瞬態本體溫度場熱平衡方程建立的理論基礎上創建了轉爐減速器齒輪模型。瞬態本體溫度場分析的研究結果為今后轉爐減速器齒輪瞬態本體溫度場的快速建模和分析提供了方法。

[1]Martins R，Seabra J，Brito A，et al.Friction coefficient in FZG gears lubricated with industrial gear oils：Biodegra-dable ester vs mineral oil[J].Tribology International，2006，39（7）：512-521.

[2]龍慧.高速齒輪傳動輪齒的溫度模擬及過程參數的敏感性分析[D].重慶：重慶大學，2001.

[3]肖望強，李威，韓建友.非對稱齒廓漸開線齒輪傳動的熱分析[J].農業機械學報，2006，37（12）:164-167.

[4]方宗德，陳國定，沈允文.斜齒輪傳動的齒面閃溫計算[J].西北工業大學學報，1992，10（2）:21-26.

[5]黃華梁，李柯.漸開線圓柱直齒輪本體溫度的邊界元法分析[J].機械設計，1993，10（1）：36-40.

[6]Gardon G，Astarita T，Carlomagno G M.Infrared Heat Transfer Measurements on a Rotating Disk[J].Optical Diagnostics in Engineering，1996（2）:1-7.

Analysis on the Transient Bulk Temperature Field of Converter Reducer Gear

Lin Jianzhu

With the improvement of gear capacity for converter reducer,the theories of gear engagement,tribology,heat transfer and Hertz contact were applied to research the change law of relative sliding velocity and friction coefficient of gear teeth. The heat flux along the line of action was calculated.By means of setting up the finite element analysis model of transient temperature field for the gear of converter reducer,the gear bulk transient temperature field was achieved.The relationship between working time and temperature gradient was analyzed and the results showed that the faster the converter reducer gear reached the heat balance,the better the gear transmission system worked.The research results provided the theory basis for the safe use of converter reducer gear and presented the method of rapid modeling and analysis for transient bulk temperature field.

converter reducer,gear,transmission,transient temperature field,finite element,scuffing load capacity

（收稿 2011－08－12責編潘娜）

林建筑，1984年畢業于東北工學院，高級工程師、副總經理，主要從事機械傳動理論和應用方面的研究工作。