用遺傳算法求最小生成樹

朱彥廷

(河池職業學院 計算機系,廣西 河池 547000)

用遺傳算法求最小生成樹

朱彥廷

(河池職業學院 計算機系,廣西 河池 547000)

以圖論和遺傳算法為基礎,給出了一個改進的求最小生成樹的算法,提出了“無性生殖”的方式,舍棄了逆轉算子,改進了換位算子,調整了選擇算子,更簡單,因而編程更容易,效率更高 .使用該算法可以在較短的時間內以較高的概率獲得一組最小或次小生成樹,而傳統算法一般只能得到一個最小生成樹 .

最小生成樹;遺傳算法;優化

1 基本原理

遺傳算法借助于生物進化機制與遺傳學原理,先隨機產生一些個體,然后進行選擇、交叉和變異操作,模擬自然界中生物的進化過程,使個體的性能不斷提高,逼近問題的最優解 .它用于求解組合優化問題非常有效,尋找最小生成樹實際也是組合優化問題,因此可以考慮使用遺傳算法 .

2 算法設計

2.1 編碼

設一無向圖共有ND個頂點,NP條邊,對邊進行編號 .一個個體是一個二進制代碼,長為NP,代表圖的一個子圖,若某位為 1,表示它所對應的邊是子圖的邊;若為 0,表示它所對應的邊不是子圖的邊 .

2.2 適應度函數

2.3 遺傳算子

交叉算子以某一概率隨機交換 2個個體的部分位,得到 2個新個體 .變異算子以某一概率隨機改變個體的某些位,得到 1個新個體 .對于本問題,它們極可能破壞個體的可行性,即得到的新個體不是只有ND-1位為 1,根本不代表一個生成樹,沒有意義,因此不能直接用這 2個算子 .

已有人對此做過研究,概括起來,他們[2-4]提出了換位算子和逆轉算子,相當于舍棄了交叉算子,對變異算子做了修改 .如果說一般遺傳算法采用的是“有性生殖”(使用交叉算子,1個新個體由 2個個體得到),那么這里的遺傳算法采用的就是“無性生殖”(舍棄交叉算子,1個新個體由 1個個體得到).生物進化了幾十億年,無性生殖仍廣泛存在于自然界中,說明它有存在的價值,遺傳算法要更好地模擬生物進化過程,也應包括這種方式 .

換位算子:隨機產生 2個換位位,對其進行換位 .以個體 011100為例,若換位位為 0、2,換位后為110100.文獻[2,4]提出換位次數隨機產生,不固定是 1,假設換位次數為 2,對 110100再次換位,可能得到的個體不如它,但它卻被丟棄了,因此應固定是 1.而若換位位為 1、2,對應的數值相同,或換位位為 1、1,換位沒有價值 .

逆轉算子:先隨機產生逆轉起始位,再隨機產生逆轉位數,如果要逆轉的部分含“1”的個數和“0”的個數相等(文獻[3]說含“1”的個數為偶數,是不準確的,其它文獻大多敘述含糊,對這個關鍵的地方只字不提),對其進行逆轉,以個體 011100為例,若逆轉起始位是 2,逆轉位數是 4,則要逆轉的部分是 1100,含“1”的個數和“0”的個數相等,逆轉后為 010011.

假設個體有n位,逆轉起始位只能為 0,1,…,n-1,逆轉位數應為偶數,最小是 2,加上相應的逆轉起始位又不大于n,編程很麻煩 .而如果要逆轉的部分含“1”的個數和“0”的個數不相等,不能進行逆轉(那將破壞個體的可行性).

各位被逆轉的概率其實是不同的 .為簡單起見,假設個體有 4位,那么逆轉起始位只能為 0、1、2,若逆轉起始位為 0,逆轉位數只能為 2、4;若逆轉起始位為 1,逆轉位數只能為 2;若逆轉起始位為 2,逆轉位數只能為 2,再假設要逆轉的部分含“1”的個數和“0”的個數相等,可以算出各位被逆轉的概率分別是 1/3,2/3,5/6,1/2,這樣可能有的位如果被逆轉能得到更好的個體,但被逆轉的概率很小;有的位如果被保留能得到更好的個體,但被逆轉的概率很大,很不合理 .

本算法舍棄了逆轉算子,對換位算子加以改進,隨機產生 1個換位位,如果該位原為 0,變為 1,為了保證新個體只有ND-1位為 1,然后向后尋找第 1個為 1的位,變為 0,如果沒找到,再從最前面尋找(一定能找到,否則意味著個體的各位全是 0,這是不可能的);如果該位原為 1,變為 0,然后向后尋找第 1個為 0的位,變為 1,如果沒找到,再從最前面尋找[一定能找到,否則意味著個體的各位全是 1(說明無向圖已是樹,那就沒必要求了),這是不可能的],這樣換位肯定有價值 .以個體 011100為例,如果產生的換位位是 1,則換位后為 001110;如果換位位是 4,換位后為 001110.

選擇算子從群體中選擇較好的個體,用來進行交叉、變異 .一般用個體的適應度與群體中個體的適應度的總和的比值作為其被選擇的概率,個體的適應度越高,被選擇的概率越大,對于本問題,較好的個體不一定產生較好的新個體,二者沒有什么關系,因此不用這種做法 .因為新個體可能不如原個體好,為更多地保存較好的個體,以便最后得到更多的最小或次小生成樹,將新群體與原群體混合,按適應度高低降序排序,選出最好的不重復的個體(約占群體數目的 80%),這充分體現了優勝劣汰的原則,再隨機產生少量新個體(約占群體數目的 20%),合起來組成下一代群體,這可以彌補舍棄逆轉算子(它改變個體的幅度大,因而對解空間的搜索能力強)帶來的不足,保持了群體的多樣性,以免出現早熟現象(進化過早停滯).

2.4 算法流程

(1)設置群體大小M、最大進化代數T;

(2)隨機生成M個個體作為初始群體,計算各個個體的適應度;

(3)如果進化代數t=T,轉到(7);

(4)變異,計算各個個體的適應度;

(5)選擇,得到下一代群體;

(6)t=t+1,轉到(3);

(7)輸出最終群體 .

3 實例

現有 10個雷達站,23條可能的光纜,如圖 1所示(括號內為光纜長度),想建立一雷達網,擬求一組光纜總長度最短或次短的方案 .采用圖論中的經典算法一般只能得到一個權為 60的最小生成樹 .應用本文算法,參數設置如下:M=10,T=200,結果如表 1所示,可獲得 8個(1～7號個體)最小或次小生成樹(權為60～62(F0為 99),9、10號個體是隨機產生的,不代表生成樹),可以結合其它因素進一步確定選擇哪一個 .

表 1 最終群體

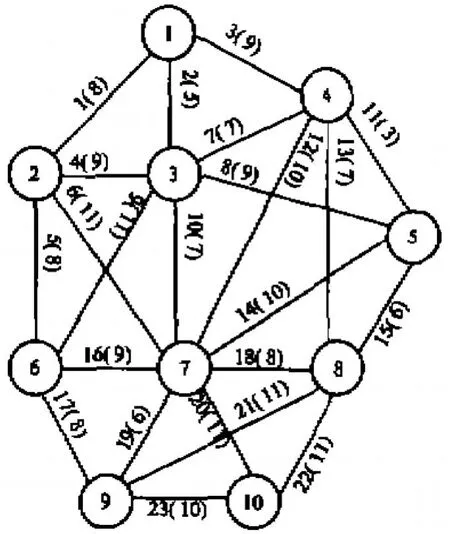
圖 1 雷達網初步連接圖

4 結語

本文提出了“無性生殖”的方式,豐富了遺傳算法的概念 .和已有的算法比,本文算法敘述清晰,舍棄了逆轉算子 (可能耗費了時間,卻不能進行逆轉),改進了換位算子 (可能耗費了時間,卻不能有效進行換位),調整了選擇算子 (可以彌補舍棄逆轉算子的缺點),更簡單,因而編程更容易,效率更高 (因為舍棄了逆轉算子,改進了換位算子,使其肯定能有效進行).應用時可以每隔幾代 (如 5、10代)計算一次選出的最好的不重復的個體的平均適應度,并和上次比較,如小于某個閾值,可以考慮停止進化,這樣更省時間 .

[1]唐策善,李龍澍,黃劉生.數據結構[M].北京:高等教育出版社,1992,137-142.

[2]周榮敏,買文寧,雷延峰.基于遺傳算法的最小生成樹算法[J].鄭州大學學報 (工學版),2002,23(1):45-48.

[3]劉志成,錢建剛.基于改進遺傳算法的最小生成樹算法[J].計算機工程與設計,2004,25(9):1620-1622.

[4]張強,李曉莉.交通選線優化算法的設計與實現[J].計算機工程與應用,2009,45(8):226-228.

A Genetic Algorithm to Determ ine theM in imum Spann ing Tree

ZHU Yan-ting

(Department of Computer Science,Hechi Vocational College,Hechi Guangxi547000,China)

Based on graphic theory and genetic algorithm,an improved algorithm to deter mine the minimum spanning tree is given,the“asexual reproduction”method introduced,the transposition operator abandoned,the transposition operator improved,and the selection operator adjusted,which makes program easier and more efficient.Using the algorithm,we can obtain a group ofminimum or less spanning trees in a shorter time and with a higher probability,while using the traditional algorithms,we can only get a minimum spanning tree.

minimum spanning tree;genetic algorithm;optimization

TP3

A

1672-9021(2010)02-0062-04

朱彥廷 (1976—),男,遼寧建昌人,河池職業學院計算機系助教,碩士,主要研究方向:遺傳算法等.

2009-12-25

[責任編輯陽崇波 ]