一類離散廣義非線性 Schr?d inger系統周期解的存在性

譚偉明,覃學文

(梧州學院數理系,中國 梧州 543002)

一類離散廣義非線性 Schr?d inger系統周期解的存在性

譚偉明,覃學文＊①

(梧州學院數理系,中國 梧州 543002)

把一些文獻討論的離散廣義非線性 Schr?dinger方程推廣到了n維空間,應用臨界點理論,得到了一類離散廣義非線性 Schr?dinger系統存在多個非零周期解的充分條件.

Schr?dinger系統 ;臨界點 ;周期解

非線性 Schr?dinger方程是現代物理和數學理論研究中的一個基本方程,對這個方程的研究在推動現代物理和數學的發展起著非常重要的作用.從數學家的觀點來看,非線性 Schr?dinger方程也具有極大的吸引力,數學家們對這個方程關注和探討的問題也是多方面的.近十多年來,許多學者對非線性 Schr?dinger方程及其應用作了深入的研究,取得了一定的成果[1-9].

文 [4]從離散非線性 Schr?dinger方程

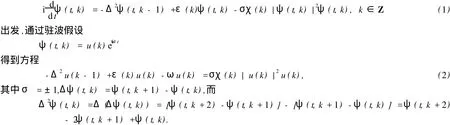
1 預備知識和變分結構

2 主要結果

下面證明系統(6)還有其它的非零T-周期解,為此只需證明泛函J(X)在ET上還有其它的非零臨界點.應用山路引理證明.

可證明泛函J滿足環繞定理的條件.由于已證明泛函J滿足 P-S條件,因此只需證明泛函J滿足環繞定理的條件(1)和(2).

即轉化為(1)的情形,由上述討論可知,泛函 -J至少有 2個臨界點,從而泛函J至少有 2個非零臨界點,于是系統(6)至少存在 2個非零T-周期解.

[1]BEREZ IN F A,SHUB IN M A.The Schr?dinger equation[M].Netherlands:KluwerAcademic Publishers,2002.

[2]ABLOW ITZM J,PR INAR IB,TRUBATCH A D.Diserete and continuous nonlinear Schr?dinger systems[M].New York:Cambridge University Press,2004.

[3]MULLER-KI RSTEN H JW.Introduction to quantum mechanics:Schr?dinger equation and path integral[M].Singapore:World Scientific Printers(S)Pte Ltd,2006.

[4]PANKOV A.Gap solitons in periodic discrete nonlinear Schr?dinger equation[J].Nonlinearty,2006,19:27-40.

[5]ALEXANDRU D IONESCU,CARLOS E KEN IG.Uniqueness properties of solutions of Schr?dinger equations[J].Journal of FunctionalAnalysis,2006,232:90-136.

[6]ALOMAR IA K,NOORAN IM SM,NAZAR R.Explicit series solutionsof some linear and nonlinear Schr?dinger equations via the homotopy analysismethod[J].Communications in Nonlinear Science and Numerical Simulation,2009,14:1 196-1 207.

[7]G IOVANNA CERAM I,R ICCARDO MOLLE.Positive solutions for some Schr?dinger equations having partially periodic potentials[J].Journal ofMathematicalAnalysis and Applications,2009,359:15-27.

[8]NAKAO HAYASH I,PAVEL INAUMK IN.Asymptotics of odd solutionsof quadratic nonlinear Schr?dinger equations[J].Journal ofMathematicalAnalysis and Applications,2009,359:146-158.

[9]KOPYLOVA E A.On the asymptotic stability of solitarywaves in the discrete Schr?dinger equation coupled to a nonlinear oscillator[J].NonlinearAnalysis,2009,71:3 031-3 046.

Existence Periodic Solution of the Generalized D iscrete Nonlinear Schr?dinger System

TAN W ei-m ing,Q IN Xue-wen
(School ofMathematics and Physics,Wuzhou University,Wuzhou 543002,China)

The generalized discrete nonlinear Schr?dinger equation discussed in some literature are extented ton-d imensional space.Using critical point theory,some sufficient conditions are obtained for the existence periodic solution of the generalized discrete nonlinear Schr?dinger system.

Schr?dinger systems;critical point theory;periodic solution

O413.1

A

1000-2537(2010)04-0046-07

2010-05-17

梧州學院科研基金資助項目 (2009B012);廣西教育廳科研基金資助項目(2008MS121);廣西自然科學基金資助項目 (桂科自 0991279)

＊通信作者,E-mail:hnsyb@126.com

(編輯 陳笑梅)