對一道多根式賽題的探究

●

(育才中學 上海 201801)

對一道多根式賽題的探究

●龔新平

(育才中學 上海 201801)

2009年全國高中數學聯賽一試的最后一道解答題中出現了含3個根式的和函數最值問題，筆者發現往屆全國聯賽也出現了類似的問題！本文將首先對該問題給出4種不同的解法，同樣的方法也適用于解決含4個或更多根式的最值求解；然后筆者還將在此問題的基礎上嘗試編擬幾道含多根式的最值問題,供讀者參考.

(2009年全國數學聯賽試題)

1 4種不同的解法

解法1(調節系數,適度放縮)一方面，由定義域為x∈[0,13]可知

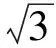
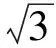
解得x=9.如取k=1，則a=6,b=3,c=2，此時

即當x=9時函數取到最大值ymax=11.

解得x<9，即

在[0,9]上單調遞增，在[9,13]上單調遞減，故最大值為f(x)max=f(9)=11，最小值為

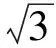
從而當x=9時，最大值為

f(u,v,w)max=f(6,3,2)=11.

在邊界處取得最小值,為

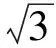
u2+2v2+3w2=66(u,v,w>0).

(1)

代入式(1)可得

此時,u=6,v=3,w=2,從而最大值為

f(u,v,w)max=f(6,3,2)=11，

在邊界處取得最小值,為

2 問題編擬

本題是由一道2003年的全國聯賽試題改編而來的.

1.7.1 有效性評價指標 ①腹痛發作天數，②腹痛程度，③伴隨癥狀，以上均于基線、治療后第1、2周記錄，治療結束評價；④中醫證候療效，基線、治療結束記錄，治療結束評價；⑤腹痛復發情況，治療結束后4周評價。以腹痛發作天數為主要評價指標。

f(x)max=f(x0).

事實上,由Mathematica數學軟件解方程(2)，易見此時

即

分析由前面的分析不難得出最大值為

f(x)max=f(37)=6+3+2+1=12，

最小值為

可知,當x>0時，

在[0,+∞)上也遞增，故