排列組合解題策略的再探究

●

(紹興市第一中學 浙江紹興 312000)

排列組合解題策略的再探究

●言利水

(紹興市第一中學 浙江紹興 312000)

排列組合是重要的知識點，也是解決概率問題的基礎工具，排列組合問題歷來是高中數學學習中的難點.通過平時做的練習題不難發現,排列組合題的特點是條件隱晦、不易挖掘、題目多變、解法獨特、數字龐大、難以驗證.因此只有熟練掌握基本的解題策略，才可以選取不同的技巧來解決問題.對于一些比較復雜的問題,我們可以將幾種策略結合起來,把復雜的問題簡單化，舉一反三，觸類旁通，進而為后續學習打下堅實的基礎.本文把排列組合問題的常用解題策略作了詳細的歸納，旨在幫助讀者突破學習難關.

1 合理分類與分步策略

例1如圖1，一環形花壇分成A,B,C,D這4塊，現有4種不同的花供選種，要求在每塊里種1種花，且相鄰的2塊種不同的花，則不同的種法總數為

( )

A．96 B．84 C．60 D．48

解可以分為3類：

因此,共有

本題還可另解：按A-B-C-D順序分步種花，可分A，C同色與不同色有4×3(1×3+2×2)=84種不同的種法.

說明解含有約束條件的排列組合問題，可按元素的性質進行分類，按事件發生的連續過程分步，做到標準明確.分步層次清楚、不重不漏，分類標準一旦確定就要貫穿于解題過程的始終.

2 相鄰元素捆綁策略

例27個人站成一排,其中甲、乙相鄰，且丙、丁相鄰,問共有多少種不同的排法？

說明要求某幾個元素必須排在一起的問題,可以用捆綁法來解決問題.即將需要相鄰的元素合并為一個元素,再與其他元素一起作排列,同時要注意合并元素內部也必須排列.

3 不相鄰問題插空策略

例3一條長椅上有7個坐位，4個人坐，要求3個空位中，有2個空位相鄰，另1個空位與這2個相鄰空位不相鄰，問共有多少種坐法？

說明元素相離問題可先把沒有位置要求的元素進行排隊，再把不相鄰元素插入中間和兩端.

4 定元定位優先排策略

例4由0,1,2,3,4,5可以組成多少個沒有重復數字五位奇數.

說明位置分析法和元素分析法是解決排列組合問題最常用也是最基本的方法.若以元素分析為主,則需先安排特殊元素,再處理其他元素;若以位置分析為主,則需先滿足特殊位置的要求,再處理其他位置;若有多個約束條件，則往往是考慮一個約束條件的同時還要兼顧其他條件.

5 定序問題倍縮空位插入策略

例57人排隊,其中甲、乙、丙3人順序一定,共有多少種不同的排法?

思考可以先讓甲、乙、丙就坐嗎?

(插入法)先排甲、乙、丙3個人,共有1種排法,再把其余4人依次插入,共有4×5×6×7=840種方法.

說明定序問題可以用倍縮法，還可轉化為空位法或插入法求解.

6 平均分組問題除法策略

例612名學生平均分為3個實習小組，3名教師各參加其中一組進行指導，則共有多少不同的分配方案？

若將本題看成是每個教師各選4名學生有如下解答.

7 名額分配問題隔板策略

例7有10個運動員名額，分給7個班，每班至少1個,有多少種分配方案？

(1)3個相同的球裝入7個盒中,有多少裝法？

(2)求方程組x1+x2+x3+x4+x5+x6+x7=10的正整數解.

(3)求方程組x1+x2+x3+x4+x5+x6+x7=3的非負整數解.

8 排列組合混合問題先選后排策略

例8有5個男生和3個女生，從中選取5個人擔任5門不同學科的科代表，求有女生但人數必須少于男生的選法數.

說明解決排列組合混合問題,先選后排是最基本的指導思想.

9 小集團問題先整體后局部策略

例9用1,2,3,4,5組成沒有重復數字的五位數,其中恰有2個偶數夾在1,5這2個奇數之間,這樣的六位數有多少個？

說明在小集團排列問題中，先整體后局部，再結合其他策略進行處理.

10 環排問題線排策略

例108人圍桌而坐,共有多少種坐法?

解圍桌而坐與坐成一排的不同點在于:坐成圓形沒有首尾之分，因此固定一人并從此位置把圓形展成直線,則其余7人共有(8-1)！種排法.

11 多排問題直排策略

例118個人排成前后2排,每排4個人,其中甲、乙在前排,丙在后排,共有多少種排法.

說明一般地,元素分成多排的排列問題,可先歸結為一排考慮,再分段研究.

12 機會均等二分策略

例12某校高二期中考試安排考7門科目,若規定語文要在數學之前考,則有多少種不同的安排順序?

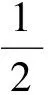
13 重復排列問題求冪策略

例137名學生爭奪5項冠軍，每項冠軍只能由1人獲得，求獲得冠軍的可能的種數.

解因為同一學生可以同時奪得5項冠軍，所以學生可重復排列，將7名學生看作7家“店”，5項冠軍看作5名“客”，每個“客”有7種住宿法.故由乘法原理得,有75種可能.

說明解決“允許重復排列問題”要注意區分兩類元素：一類元素可以重復，另一類不能重復.把不能重復的元素看作“客”，能重復的元素看作“店”，再利用乘法原理直接求解.

允許重復的排列問題的特點是以元素為研究對象，不受位置的約束，可以逐一安排各個元素的位置.一般地,n個不同的元素沒有限制地安排在m個位置上的排列數為mn種.

14 正難則反排除策略

例14從0,1,2,3,4,5,6,7,8,9這10個數字中取出3個數，使其和為不小于10的偶數,不同的取法有多少種？

解直接求不小于10的偶數很困難,可用總體排除法.

說明對于含有否定詞語的問題，還可以從總體中把不符合要求的減去，此時應注意既不能多減也不能少減.此題若是直接去考慮的話,就要將問題分成好幾種情況,容易造成遺漏或者重復的情況.如果從此問題相反的方面去考慮的話,不但容易理解,而且在計算中也非常簡便.

15 一一對應剩余策略

例15袋中有5分硬幣23個,1角硬幣10個,若從袋中取出2元錢,則有多少種取法?

解把所有的硬幣全部取出來,將得到

0.05×23+0.10×10=2.15元,

說明此題是一個組合問題,若是直接考慮取錢的問題的話,則情況比較多,也顯得比較凌亂,難以理出頭緒來.但是如果根據組合數性質考慮剩余問題的話,就會很容易解決問題.

在組合問題中,有多少種取法就有多少種剩余法,它們是一一對應的,因此當求取法困難時,可轉化為求剩余法.

16 實際操作窮舉策略

例16設有編號1,2,3,4,5的5個球和編號1,2,3,4,5的5個盒子,現將5個球投入這5個盒子內,要求每個盒子放1個球，并且恰好有2個球的編號與盒子的編號相同,有多少種投法？

說明題中附加條件增多，當直接解決困難時，用實驗逐步尋求規律有時也是一種行之有效的方法.

17 自身回避問題樹圖策略

例17同一寢室4個人,每人寫1張賀年卡集中起來,然后每人各拿1張別人的賀年卡，則4張賀年卡不同的分配方式有多少種？

解設有甲、乙、丙、丁4個人,則甲拿乙的情況可用樹圖表示如下:

甲拿乙的情況有3種,同理甲拿丙或丁的情況也各有3種.

說明對于條件比較復雜的排列組合問題，不易用公式進行運算，例如本題利用枚舉法或畫出樹狀圖會收到意想不到的結果.

18 分解與合成策略

例1830 030能被多少個不同的偶數整除?

解先把30 030分解成質因數的乘積形式:

30 030=2×3×5×7×11×13.

依題意可知,偶因數必先取2,再從其余5個因數中任取若干個組成乘積，所有的偶因數的個數為

說明分解與合成策略是排列組合問題的一種最基本的解題策略,把一個復雜問題分解成幾個小問題逐一解決,然后依據問題分解后的結構,用分類計數原理和分步計數原理將問題合成,從而得到問題的答案.

19 轉化與化歸策略

例1925個人排成5×5方隊,現從中選3個人,要求這3個人不在同一行也不在同一列,不同的選法有多少種？

圖2

說明當處理復雜的排列組合問題時,可以把一個問題退化成一個簡要的問題，通過解決這個簡要的問題找到求解的方法，從而進一步解決原來的問題.

20 集合劃分策略

例20從0，1，2，3，4，5中任取3個，可以組成多少個沒有重復數字且能被6整除的三位數.

解所求三位數有被6整除的特征，就是要被3和2整除，這個要求可分解為3個數之和要被3整除，而末位是偶數.因此選取的3個數中必須有偶數而且它們的和要能被3整除,有(0，1，2)，(0，1，5)，(0，2，4)，(1，2，3)，(2，3，4)，(2，4，5)這6類.

對各類進行排列計算，這是要先定末位(偶數)，再定首位(非0):

因此共有19個滿足題意的數字.

說明研究有約束條件的排列問題，須要緊扣題目所提供的數字特征、結構特征，進行推理，分析求解.

例21從集合{1，2，3，…，10}中，選出由5個數組成的子集，使得這5個數中的任何2個數的和不等于11，則這樣的子集共有

( )

A.10個 B.16個 C.20個 D.32個

解將和為11的數分組有(1，10)，(2，9)，(3，8)(4，7)，(5，6)共5組，只要從這5個集合中各取1個元素就符合題意，每個集合有2種取法，故有25=32個子集.

說明將集合中的元素進行劃分，構造所需要的集合，是排列組合中有較高要求的問題.