線性規劃在求解不等式范圍問題中的應用

●

(武陟縣第一中學 河南武陟 454950)

線性規劃在求解不等式范圍問題中的應用

●王雷義

(武陟縣第一中學 河南武陟 454950)

不等式范圍的求解是一個重點內容，在利用不等式性質求解不等式的范圍時，要正確理解其性質，切不可盲目濫用，應注意不等式的應用方向.在解題過程中，有時會出現似乎可以運用不等式性質解題，且出現范圍擴大、性質失效的現象.如果能夠轉換思路，利用數形結合的方法求解，往往可以避免錯誤的發生，從而達到求解的目的.因此用線性規劃解決這類問題顯然是一種比較好的方法，下面就這個問題略舉幾例說明.

例1已知函數f(x)=ax2+bx，1≤f(-1)≤2，2≤f(1)≤4，求f(-1)的取值范圍.

解法1利用不等式的性質求解.

錯解因為f(-1)=a-b，f(1)=a+b,所以由題意得

由不等式組利用不等式性質進行加減消元得

從而由f(-2)=4a-2b,可得

3≤f(-2)≤12.

錯因分析不等式的性質除了個別外，其他的條件和結論間都不是充要條件，而只是充分條件.在解題中，使用性質定理，尤其是反復使用性質定理會使求解的范圍擴大、變量的范圍擴大，從而出現增根.本題正是因為多次利用了不等式性質中的加法法則(同向可加性)，而此法則是單向的，不具有可逆性，從而使a,b的范圍擴大，這樣f(-2)的范圍也隨著擴大了.

因為a-b,a+b中的a,b不是獨立的，而是相互制約的，所以若將f(-2)用a-b和a+b表示，則問題可以得解.

正解設f(-2)=xf(-1)+yf(1)(x,y為待定系數)，則

4a-2b=x(a-b)+y(a+b)，

即

4a-2b=(x+y)a-(x-y)b.

于是

x=3,y=1,

從而

f(-2)=3f(-1)+f(1).

由題意

1≤f(-1)≤2,2≤f(1)≤4,

可得

5≤3f(-1)+f(1)≤10,

故

5≤f(-2)≤10.

點評嚴格依據不等式的基本性質和運算法則，是正確解決此類題的保證.

如果利用數形結合的方法解題,那么線性規劃就不失為一種絕妙的好方法.

解法2利用線性規劃求解.

建立線性約束條件，由1≤f(-1)≤2，可得

1≤a-b≤2；

由2≤f(1)≤4，可得

2≤a+b≤4.

因此可得線性約束條件不等式組

圖1

線性目標函數為f(-2)=4a-2b，如圖1所示，過點(0，0)作直線l0:4a-2b=0.把直線l0向右下方平行移動到位置l′時，直線經過點A，此時f(-2)=4a-2b取得最小值.解方程組

f(-2)min=5.

把直線l0向右下方平行移動經過點C，此時f(-2)=4a-2b取得最大值.解方程組

f(-2)max=10,

故

5≤f(-2)≤10.

點撥通過線性規劃求f(-2)的最大值和最小值,避免了反復使用性質定理而導致范圍擴大，出現增根的現象，結果直觀明了，不易出錯.

解法1利用不等式的性質求解.

從而

又由α<β，可得

山水集團單筆債券未按時兌付直接導致其他債務交叉違約,不但會影響到債券市場正常的運行秩序，還會對市場參與主體和投資者的切身利益以及中介機構的信譽帶來較大的影響。另外，商業銀行的貸款也會由于其資金緊張，安全性難以保障。一旦出現貸款違約后，又會引起債權銀行提前收回貸款，進一步加劇了企業兌付債券的難度。如企業資金鏈斷裂，最后可能出現債權銀行和債券持有人權益同時遭受較大損失的局面。

解法2利用線性規劃求解.

建立線性約束條件，由題意可得不等式組

圖2

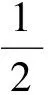
得

即

點評利用線性規劃解答此題，條理清晰，簡單明了.

思維導引由題目可獲得的信息是：利用已知條件(字母的取值范圍)求代數式的范圍.

本題可利用不等式的可加性和可乘性求解.

解法1利用不等式的性質求解.

由6

8

因為-3<-b<-2,所以

3

解法2利用線性規劃求解.

建立現行約束條件.由題意可得不等式組

圖3

(1)如圖3,作直線a+b=0,把直線a+b=0向右上方平移經過點A(6,2)，取得最小值，即

Zmin=6+2=8，

經過點C(8,3)取得最大值，即

Zmax=8+3=11,

所以

8

(2)

作直線a-b=0，把直線a-b=0向右下方平行移動經過點D(6,3)，取得最小值，即

經過點B(8,2)取得最大值，即

所以

3

點評本題用線性規劃求解不如用不等式性質求解簡單，但也體現出以數變形的直觀性，再次說明了線性規劃在解決不等式范圍問題中的優越性.

華羅庚曾說過：“數缺形時少直觀，形少數時難入微.”數形結合思想的妙處對于求解不等式范圍問題中同樣起著重要作用.我們知道，函數圖像和不等式有著密切的聯系,因此利用數形結合可以使問題直觀明了，從而更能形象地解決問題.

不等式問題因其覆蓋知識點多，方法也多種多樣，但其核心思想還是等價轉化.抓住了這點，才能以“不變應萬變”，當然這還需要我們不斷地去領悟、體會和總結.