利用局部模型估算物性數(shù)據(jù)

劉存玉

淄博職業(yè)學(xué)院 淄博 255013

有時(shí)有必要設(shè)計(jì)一個(gè)局部模型來(lái)計(jì)算在一個(gè)有限的(通常是狹窄的)溫度、壓力和組成范圍內(nèi)的物性數(shù)據(jù)。建立局部模型的目的有兩個(gè)：①簡(jiǎn)便；②在相對(duì)較窄的溫度和壓力范圍內(nèi)具有較高的準(zhǔn)確度，其中簡(jiǎn)便是第一位的。例如，控制臺(tái)板上的電子計(jì)算器可能只能進(jìn)行加減乘除運(yùn)算，而無(wú)對(duì)數(shù)、三角之類的計(jì)算功能。如果模型公式比較復(fù)雜，那么在操作現(xiàn)場(chǎng)計(jì)算可能就不方便。當(dāng)然，如果手頭的計(jì)算工具具有數(shù)據(jù)儲(chǔ)存和高級(jí)復(fù)雜的運(yùn)算功能，那也就很可能無(wú)需使用局部模型公式。然而，也不能為了簡(jiǎn)便就忽視公式的準(zhǔn)確性，畢竟不準(zhǔn)確的模型是無(wú)用的。

所謂局部是指模型建立所對(duì)應(yīng)的操作條件。局部條件往往不是隨意設(shè)定的，而是決定于所處的工藝、設(shè)備狀況以及其他實(shí)際情況。模型的建立要限定在設(shè)定的局部條件內(nèi)。

局部模型說(shuō)到底其實(shí)就是以一定的數(shù)據(jù)為基礎(chǔ)的近似關(guān)系式。這些數(shù)據(jù)可能來(lái)自于物性手冊(cè)[4]、模擬程序或其他軟件、實(shí)驗(yàn)數(shù)據(jù)、工廠數(shù)據(jù)或其他途徑。

建立局部模型，首先要有可靠的理論依據(jù)，再設(shè)定模型應(yīng)該具有怎樣的簡(jiǎn)單程度，然后利用數(shù)學(xué)的和物理的近似關(guān)系式進(jìn)行簡(jiǎn)化計(jì)算，直到取得較為理想的結(jié)果。

有時(shí)候憑直覺就可以得到一個(gè)好的局部模型，特別是將數(shù)據(jù)作圖可能會(huì)揭示出需要的函數(shù)關(guān)系。如果數(shù)據(jù)看上去具有線性關(guān)系，那么就嘗試用一個(gè)線性函數(shù)，而不管理論上有何種關(guān)系。

設(shè)計(jì)人員必須對(duì)建立的局部模型的局限性心中有數(shù)，不要將其外推。如果需要的精確度大于當(dāng)初設(shè)計(jì)局部模型時(shí)設(shè)定的準(zhǔn)確度，則不要用其進(jìn)行計(jì)算。

1 氣體密度模型

氣體流量的控制在很多情況下決定于氣體的密度。對(duì)某些計(jì)算而言，使用理想氣體定律就足夠了。然而，對(duì)非理想狀態(tài)，利用包含壓縮因子的公式計(jì)算可得到更好的結(jié)果。氣體的密度可以用式(1)計(jì)算：

ρ=MP/(ZRT)

(1)

式中，ρ為密度，kg/m3；M為摩爾質(zhì)量，kg/kmol；P為壓力，kPa；Z為壓縮因子，無(wú)因次；R為氣體常數(shù)，8.314 m3·kPa/(kmol·K)；T為溫度，K。

現(xiàn)在就以維里方程建立壓縮因子的局部模型。

維里方程是一個(gè)具有堅(jiān)實(shí)動(dòng)力學(xué)理論基礎(chǔ)的狀態(tài)方程[1]。它可寫成式(2)的形式：

(2)

式中，B、C和D為維里系數(shù)。

對(duì)低壓氣體，通常截取公式中的第一、二項(xiàng)就足夠了：

(3)

式中，B為第二維里系數(shù)，它是溫度的函數(shù)，而與壓力無(wú)關(guān)。

對(duì)純物質(zhì)，有作者推導(dǎo)出一個(gè)相對(duì)簡(jiǎn)單的求解第二維里系數(shù)的關(guān)聯(lián)式：

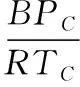
(4)

(5)

(6)

式中，ω為離心因數(shù)；下標(biāo)C代表臨界點(diǎn)；下標(biāo)R代表對(duì)比條件(TR=T/TC)。

將式(5)、式(6)代入式(4)得：

(7)

對(duì)一定的物質(zhì)，式(7)中的TC、PC和ω都是常數(shù)，因此可將式(7)改寫為更一般的表達(dá)式：

(8)

式中，常數(shù)An(n=1，2，3，…)為相關(guān)常數(shù)的組合，可以根據(jù)具體條件計(jì)算出來(lái)。

將式(8)代入式(3)，就得到壓縮因子的第一個(gè)局部模型：

(9)

實(shí)際上，從這一點(diǎn)就開始簡(jiǎn)化了。由于是在有限范圍內(nèi)使用，所以可以進(jìn)行近似處理。

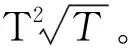
(10)

由此得：

T2.6≈T2.5≈aT2+bT3

(11)

把這些近似式代入式(9)，得到第二個(gè)局部模型關(guān)系式：

(12)

注意在導(dǎo)出的該表達(dá)式中沒有四次項(xiàng)。可以進(jìn)一步將其作為溫度倒數(shù)的指數(shù)數(shù)列加以表述，就如式(13)所示：

(13)

在滿足要求的準(zhǔn)確度的情況下，為避免不必要的復(fù)雜，限制公式中包含的項(xiàng)數(shù)為好。當(dāng)然，在更寬的溫度和壓力范圍內(nèi)，很可能就需要更多的數(shù)列項(xiàng)數(shù)。

簡(jiǎn)單加和數(shù)列公式的優(yōu)點(diǎn)在于它沒有使代數(shù)運(yùn)算復(fù)雜化的分?jǐn)?shù)指數(shù)，缺點(diǎn)是因簡(jiǎn)化而不夠嚴(yán)密。例如在式(13)增加沒有理論基礎(chǔ)的第4項(xiàng)，必須通過(guò)對(duì)一些數(shù)據(jù)進(jìn)行回歸來(lái)計(jì)算校正系數(shù)Ai。

盡管該數(shù)列模型在寬的溫度和壓力范圍內(nèi)的準(zhǔn)確度不很高，但是這里要找的也不過(guò)是在相對(duì)較窄狀態(tài)條件下具有合理準(zhǔn)確度的模型，下面通過(guò)實(shí)例來(lái)說(shuō)明。

表1的數(shù)據(jù)取自一套甲烷物性數(shù)據(jù)表[2]，這是建立模型的基礎(chǔ)數(shù)據(jù)。利用表1數(shù)據(jù)建立一個(gè)在有限溫度和壓力范圍內(nèi)甲烷的壓縮因子模型。

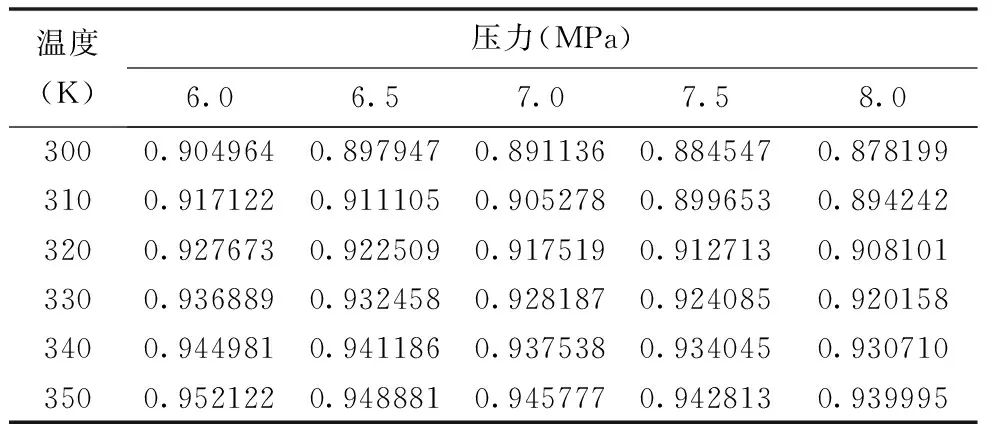
表1 甲烷壓縮因子表

1.1 解法一

(1)利用更嚴(yán)格的模型式(9)，得到式(14)：

(14)

和表1數(shù)據(jù)核對(duì)，由該公式計(jì)算出的數(shù)據(jù)誤差為：AE=0.01%，AAE=0.13%，MaxE=0.28%，可見符合程度較好。考慮到溫度范圍是隨意選取的，因此該局部模型計(jì)算數(shù)據(jù)和表1中數(shù)據(jù)的一致性較理想。當(dāng)然，這并不代表所有情況都有這樣的準(zhǔn)確度。

(2)AE為平均誤差，其定義為：

式中，v(i)為建立模型所采用的數(shù)據(jù)值；e(i)則是在相同條件下利用建立的模型計(jì)算出的對(duì)應(yīng)值(即估算值)；NP為取值點(diǎn)的個(gè)數(shù)。可見，AE可正可負(fù)。

(3)AAE為絕對(duì)平均誤差，其定義為：

顯然，AAE只能為正。若AE小而AAE相對(duì)較大，則說(shuō)明在建立模型所采用的數(shù)值和對(duì)應(yīng)的估算值之間存在系統(tǒng)偏差。

(4)MaxE是最大誤差，取下式中的最大值，它表示模型與建立模型所使用數(shù)據(jù)間的最大偏差：

1.2 解法二

以式(13)為計(jì)算基礎(chǔ)進(jìn)行檢驗(yàn)。利用給定的壓縮因子數(shù)據(jù)，對(duì)該式進(jìn)行5項(xiàng)指數(shù)數(shù)列擴(kuò)展而得的回歸數(shù)據(jù)見表2。

表2 平均絕對(duì)誤差一覽表

表2中AAE數(shù)值清楚地表明，數(shù)列項(xiàng)超過(guò)兩項(xiàng)就對(duì)局部模型的準(zhǔn)確度幾乎沒有什么貢獻(xiàn)。因此，最后所得到的局部模型為式(15)：

(15)

式中，P為壓力，MPa；T為溫度，K。

對(duì)此模型，AE=0.02%，AAE=0.13%，MaxE=0.31%，表明和前述更嚴(yán)格的(也更復(fù)雜的)模型相當(dāng)。

查驗(yàn)式(15)的準(zhǔn)確度，用其估算35℃，6.28MPa下的壓縮因子，結(jié)果見式(16)：

(16)

該結(jié)果與由表1雙線性內(nèi)插法所得數(shù)據(jù)之間的誤差值為0.2%。

注意，上述模型的建立是假定過(guò)程無(wú)相變發(fā)生，否則不能使用。

2 氣體的焓

對(duì)焓建立局部模型需要以理想氣體焓變公式為基礎(chǔ)來(lái)進(jìn)行一些新的推理。式(17)為理想氣體焓變的確切表達(dá)式。

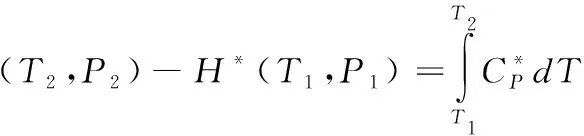
(17)

式中，H為焓；上標(biāo)*代表理想氣體狀態(tài)；CP為等壓熱容。

眾所周知，理想氣體的焓與壓力無(wú)關(guān)。一般可將理想氣體的熱容表示為溫度的多項(xiàng)式。因此，焓的一個(gè)合乎邏輯的局部模型可以用式(18)表達(dá)：

H=a+bT+cT2+dT3+……

(18)

通常，一個(gè)包含三次方的多項(xiàng)式可適用于很寬的溫度范圍。四次方多項(xiàng)式可用于0～1000K的范圍。只要壓力變化不大，這樣的模型就已足夠準(zhǔn)確。

壓力對(duì)理想氣體的焓有影響，建立模型時(shí)可將這一點(diǎn)考慮進(jìn)去。例如，利用Peng-Robinson(PR)狀態(tài)方程[3]來(lái)計(jì)算組成為表3的酸性氣體混合物的焓，見表4。

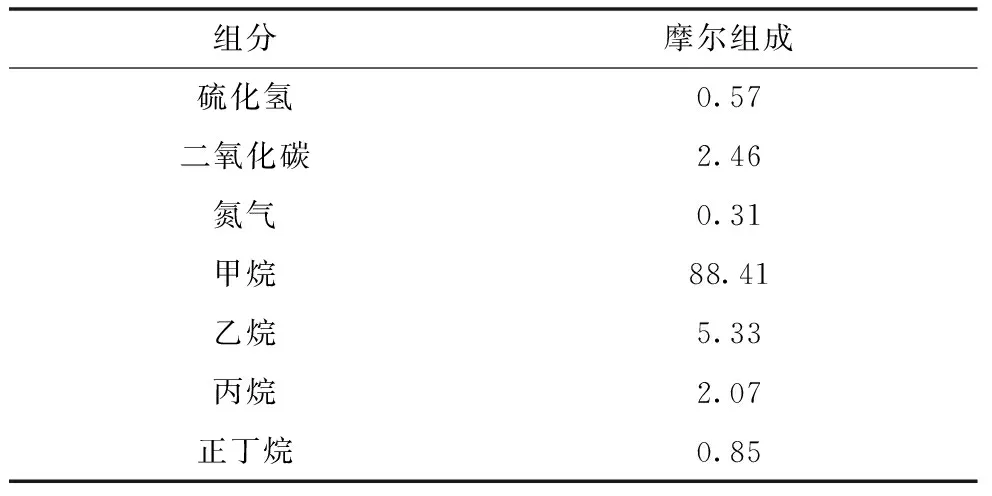
表3 某種酸性氣體混合物的組成 (%)

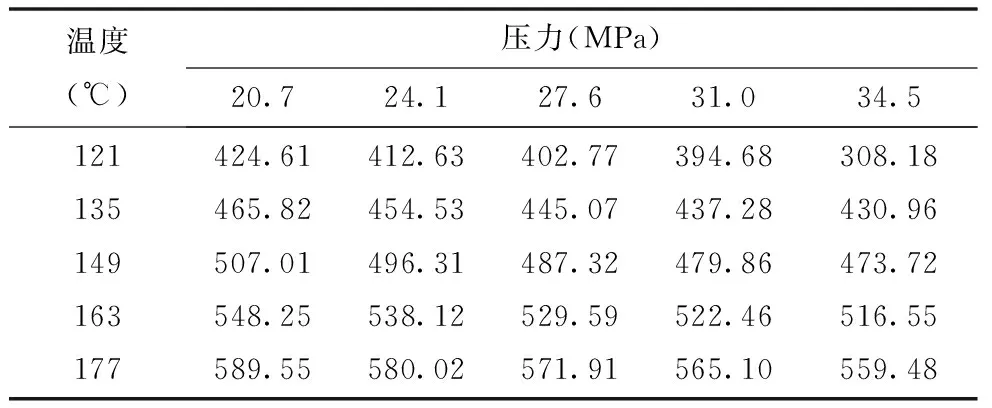
表4 某酸性氣體混合物的焓 (kJ/kg)

現(xiàn)分步建立模型。如果焓是溫度的線性函數(shù)，與壓力無(wú)關(guān)，那么可推出近似式(19)：

H=37.02+3.04t

(19)

式中，H為焓，kJ/kg；t為溫度，℃。

該模型的誤差為：AE=-0.08%，AAE=2.15%，MaxE=4.70%。而式(20)為二次項(xiàng)模型：

H=38.25+3.02t+5.85×10-5t2

(20)

其誤差分別為：AE=-0.13%，AAE=2.16%，MaxE=4.66%。

對(duì)上述線性模型和二次模型而言，單純從其AE值較小來(lái)判斷，兩個(gè)模型均具有不錯(cuò)的相符度。然而，其相對(duì)較大的AAE值顯示，在模型和數(shù)據(jù)之間存在系統(tǒng)誤差。

最后，在模型中加入一個(gè)壓力項(xiàng)P(單位為MPa)，得到方程式(21)：

H=38.25+3.02t+5.85×10-5t2+1721.3/P

(21)

該模型的誤差為：AE=-0.00%，AAE=0.16%，MaxE=0.50%。同前面兩個(gè)壓力無(wú)關(guān)的模型相比，該式有了非常顯著的改進(jìn)，因?yàn)閺谋?可清楚看出焓與壓力有關(guān)。

3 氣體的粘度

根據(jù)動(dòng)力學(xué)理論，理想氣體的粘度與溫度的平方根成正比，而與壓力無(wú)關(guān)。

(22)

這是建立關(guān)聯(lián)式的良好基礎(chǔ)。一般地使用平方根函數(shù)很可能是最好的，但是，就其應(yīng)用場(chǎng)合和簡(jiǎn)單計(jì)算工具而言，有必要尋求一個(gè)線性溫度函數(shù)。

式(10)表示將溫度的平方根表示為線性函數(shù)的近似關(guān)系式。因此，局部模型就簡(jiǎn)單地變?yōu)椋?/p>

μ=δ+λT

(23)

以低壓下的氫氣為例，其粘度見表5。

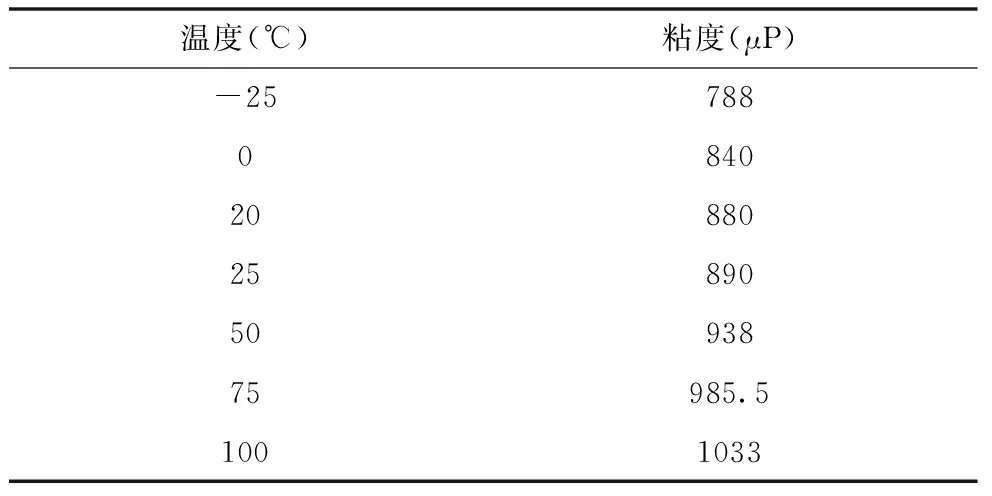
表5 低壓下氫氣粘度

像很多低壓氣體一樣，氫氣粘度是隨溫度的升高而增加的。

若按線性關(guān)系構(gòu)建模型，可得到函數(shù)關(guān)系見式(24)：

μ=306.5+1.95T

(24)

式中，μ為粘度，cP；T為溫度，K。

該線性模型的AE=0.00%，AAE=0.15%，MaxE=0.34%。誤差相當(dāng)小，所以線性模型在大多數(shù)情況下使用是合適的。

如前所述，理想氣體的粘度與壓力無(wú)關(guān)。然而，真實(shí)氣體的粘度卻隨壓力的增加而增加。這一現(xiàn)象可用式(25)表示。

μ=f(T)+AP

(25)

當(dāng)設(shè)計(jì)包含壓力的氣體粘度模型時(shí)，最簡(jiǎn)單的方法是先將數(shù)據(jù)作圖，直觀上看對(duì)壓力的依賴性。因篇幅關(guān)系，在此不舉實(shí)例。

4 液體的粘度

對(duì)液體粘度，還沒有基于什么基本原理的比較好的理論。但我們都知道，液體粘度是隨溫度的升高而降低的，用式(26)來(lái)表示：

lnμ=A+BT

(26)

該式含有對(duì)數(shù)，這對(duì)局部模型來(lái)說(shuō)是不希望有的。為避免對(duì)數(shù)的存在，將該式變化為式(27)的指數(shù)形式：

(27)

對(duì)該式采用近似關(guān)系見式(28)：

(28)

把式(27)改寫為式(29)：

(29)

這是溫度倒數(shù)的指數(shù)數(shù)列。因此，局部模型就可壓縮為式(30)：

(30)

為簡(jiǎn)化起見，將常數(shù)命名為Ci。項(xiàng)數(shù)的多少影響局部模型的準(zhǔn)確性。僅留一項(xiàng)(即假定粘度是個(gè)常數(shù))近似程度不好。一般情況下，保留三項(xiàng)可能就足夠。如果壓力范圍不太寬，那么一般可忽略壓力的影響。然而，增加壓力，液體粘度也趨于增加。作為第一次近似，可假定粘度與壓力成正比。因此，一個(gè)類似于式(25)的模型就可由式(31)來(lái)表示：

(31)

以建立計(jì)算液態(tài)二氧化碳粘度的局部模型為例，一定溫度和壓力范圍內(nèi)液態(tài)二氧化碳的粘度見表6。

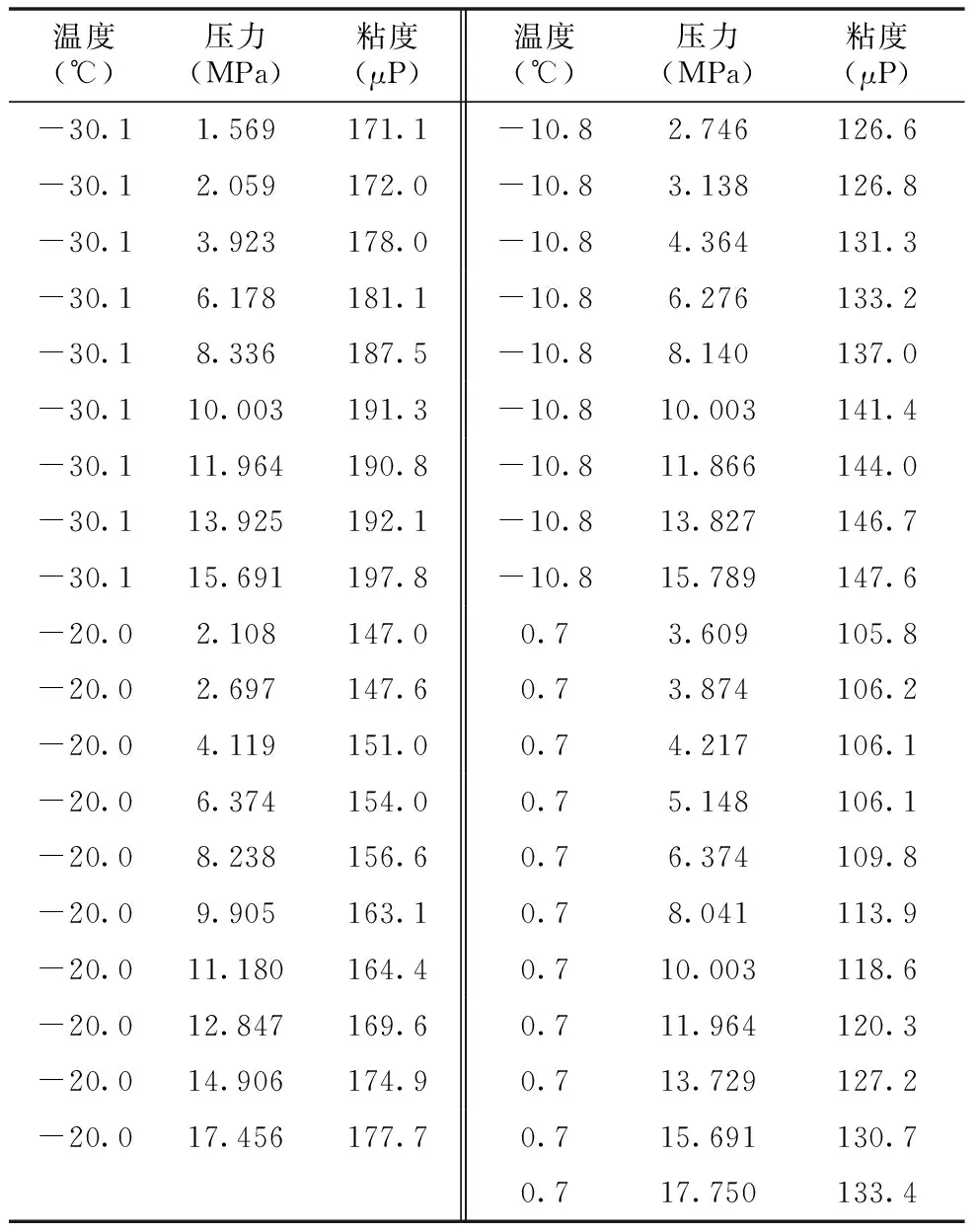
表6 液態(tài)二氧化碳的粘度

如果將表中數(shù)據(jù)作圖，可以看出溫度不變時(shí)，當(dāng)壓力增加，粘度也增加，而且?guī)缀躏@示出線性關(guān)系。并且線性關(guān)系似乎與溫度無(wú)關(guān)，就是說(shuō)，對(duì)所有等溫線，其斜率近乎相同。

利用這些信息以及上面的近似關(guān)系式(31)，就可以建立起局部模型式(32)：

μ=-458.8+(1.524×105)/T+1.951P

(32)

式中，μ為粘度，μP；T為溫度，K；P為壓力，MPa。

該模型對(duì)數(shù)據(jù)具有良好的相符程度：AE=-0.06%，AAE=0.92%，MaxE=3.60%。

5 需要注意的事項(xiàng)

(1)正因?yàn)榫植磕Ｐ秃?jiǎn)單，所以就不應(yīng)超出限定的條件范圍使用。得出的模型是針對(duì)單相體系的，不要企圖將對(duì)氣體推出的模型通過(guò)關(guān)聯(lián)來(lái)估算液體的性質(zhì)，反之亦然。

(2)要避開臨界點(diǎn)附近的區(qū)域，因?yàn)樵谂R界點(diǎn)區(qū)域的物性變化很快。即便是嚴(yán)格的模型，在臨界點(diǎn)附近區(qū)域使用也難得到良好的結(jié)果。

參 考 文 獻(xiàn)

1 Van Ness, H.C.et al, Classical Thermodynamics of Nonelectrolyte Solutions with Applications to Phase Equilibria [M].McGraw-Hill, New York, 1982.

2 Wagner, W.and de Reuck K. M., Methane. International Thermodynamic Tables of the Fluid State-13 [M].Blackwell Science, Oxford, UK, 1996.

3 Peng, D. Y.and Robinson, D.B.A New Two-constant Equation of State [J]. Ind. Eng. Chem. Fund., 15, 1976.

4 王松漢主編. 石油化工設(shè)計(jì)手冊(cè)[M].北京: 化學(xué)工業(yè)出版社，2004.