二次曲率引力場方程非球對稱解

曹學靜,許揚,陳貽漢

(湖北大學 物理學與電子技術學院,湖北 武漢 430062)

現代宇宙觀測表明,宇宙中幾乎所有旋渦星系的旋轉曲線都趨于平坦[1],此觀測事實與旋渦星系已有的發光物質的分布相矛盾；對引力透鏡效應的觀測發現,透鏡星系中總的發光物質質量遠小于觀測所推算得到的質量[2].鑒于牛頓引力理論對這些宇宙觀測事實無法解釋的困難,有人提出在Einstein廣義相對論引力作用量中加上時空曲率平方項來解釋旋渦星系旋轉曲線趨于平坦與引力透鏡質量問題.文獻[3]從引力規范理論角度提出了一含有曲率平方項的拉格朗日函數,給出了二次曲率引力場方程,文獻[4-5]在弱場線性近似條件下,求得二次曲率引力場方程的靜態球對稱解,其中包含了兩項Yukawa勢,表明二次曲率引力場作用量中的曲率平方項在小范圍對引力相互作用給出弱的修正.本文中在弱場線性近似條件下,首先將二次曲率引力場方程分解為3個二階線性偏微分方程,通過這3個偏微分方程的解得到二次曲率引力場方程的一般引力推遲勢解；然后利用球諧函數將二次曲率靜態時空作多偶極矩展開,求得非球對稱靜態二次曲率引力場,討論有質標量引力場和有質張量引力場對廣義相對論的局域修正.

1 二次曲率引力場方程的推遲勢解

(1)

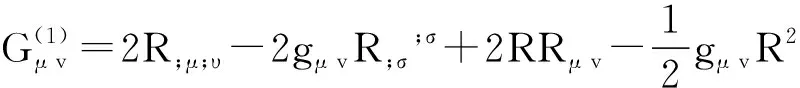
考慮弱場,時空流形M的度規張量gμ v可寫成 gμ v=ημ v+hμ v

(2)

式中ημ v為平坦時空的Mikowski度規,hμ v為小的擾動.按文獻[5],方程(1)的弱場線性近似解為

(3)

(4)

的解,ψμ v和φ分別是場方程

(5～6)

方程(4)～(6)的波動解分別為

(7)

(8)

(9)

2 靜態時空的球多偶極矩展開

對于靜止松散的物質系統(壓強p=0),方程(4)～(6)的解(7)～(9)式簡化為

(10)

(11)

(12)

式中

(13)

這里ρ(x)為物質系統的靜止質量密度,uμ為四維速度.

(14)

(15)

式中Il(x)和Kl(x)分別為l階第一類和第二類虛宗量貝塞爾函數,腳指標i=0,1.

下面我們僅考慮物質系統外部的引力場.

將(13)和(14)式代入(10)式,我們有

(16)

其中

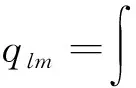
(17)

定義為Einstein引力場的多偶極矩.

同理,將(13)和(15)式代入(11)式,有質標量場可寫成

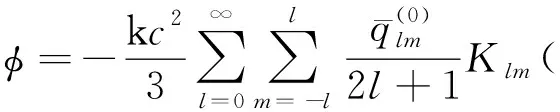
(18)

類似地,(13)和(15)式代入(12),可將有質張量場寫成

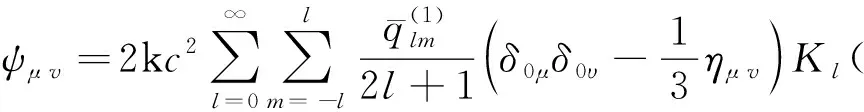
(19)

其中

(20)

(21)

利用(16)、(18)和(19)式,將(21)式引力勢寫成球諧函數的展開形式

(22)

虛宗量貝塞爾函數Kl(x)為單調衰減函數,x→∞時,Kl(x)→0.因此,當參數λ0和λ1趨于無窮,或r→∞,(22)式簡化為

(23)

此為牛頓引力勢的多極矩展開表達式.

3 結論

參考文獻:

[1] Faber S M, Gallagher J S.Masses and mass-to-light ratios of galaxies[J].Ann Rev Astron. Astrophys,1979,17:135-187.

[2] Dar A. Tests of general relativity and Newtonian gravity at large distances and the dark matter problem[J]. Nucl Phys B Proc Suppl,1992,B28:321-326.

[3] 陳貽漢,邵丹,邵亮,等.引力的曲率平方理論[J].數學物理學報,2002,22A(4):477-481.

[4] 肖明,龍蕓,鄧永菊.曲率平方引力場方程的靜態軸對稱解[J].湖北大學學報:自然科學版,2008,30(3):257-259.

[5] Chen Yi han, Shao Chang gui. Precession of orbiting gyroscope in higher-order gravitational field caused by rotating body[J].Intern J of Theor Phys,2002,41(7):1377-1387.