一道競賽題的多角度思考

●

(盱眙中學 江蘇盱眙 211700)

同一個數學問題，不同的認識角度將會帶來不同的解題思路，這就需要我們在日常的解題過程中，善于變換角度，從不同的層面分析問題，把握問題的實質.筆者通過以下一道試題的多角度思考，從中展示數學思想方法的精妙，從平凡中顯現不平凡的數學魅力，讓大家體會數學美之所在．

題目求滿足下式的銳角x:

思路1轉化思想——構造余弦定理.

解法1原式可化為

圖1

∠BCD=90°-x．

如圖1，得

|AE|+|BE|=4≥|AB|.

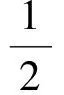
即

1=sin(x+30°),

解得

x=60°.

思路2轉化思想——聯系柯西不等式.

解法2由題意可得

16,

評注柯西不等式在不等式中的運用非常廣泛，應用它往往可以簡化運算量．

思路3方程思想——構造方程.

解法3可以利用條件進行分子有理化，建立另一方程的形式，通過方程組消元求解．

因此

從而

于是

解得

x=60°.

評注該解法由學生熟悉的分子有理化入手，再過渡到方程思想，思路如行云流水般自然.

思路4化繁為簡——樸素的化簡運算．

解法4原式可化為

兩邊平方得

即

兩邊平方得

即

sin(x+30°)=1，

解得

x=60°．

思路5消元思想.

由cos2x+sin2x=1得

a4-12a3+54a2-108a+81=0,

即

(a-3)4=0，

解得

a=3，

從而

解得

x=60°.

思路6數形結合思想——幾何法.

從幾何的角度考代數問題，可以使問題存現的方式更生動．對于本題，可以從不同的角度來考慮：一是利用兩點間公式轉化成直線，再利用點在直線上求解．二是用兩點間距離轉化后，結合余弦定理，建立等式，實現問題的求解．

解法6原式可化為

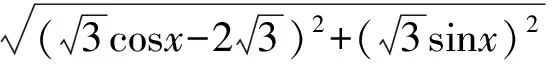
|PA|+|PB|=4.

由|AB|=4，得點P在AB上，從而AB的方程為

則

解得

x=60°．

解法7原式可化為

圖2

(1)

由余弦定理知

因此

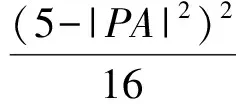
即

令|AP|=t，則

即

解得

從而

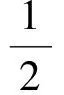
解得

x=60°．

評注數形結合思想能將代數問題生動、形象地呈現出來，因此平時要有意識地運用數形結合思想解題．