分類討論 數形結合 解題賞析
——2010年浙江省數學高考自選模塊解題體驗

●

(溫嶺中學 浙江溫嶺 318000)

分類討論數形結合解題賞析——2010年浙江省數學高考自選模塊解題體驗

●孫海琴

(溫嶺中學 浙江溫嶺 318000)

2010年浙江省數學高考自選模塊“數學史與不等式選講”考查的是含參數的絕對值不等式.作為選拔性的題目，含參數的絕對值不等式有一定的難度，需要對參數進行合理地分類討論，在討論過程中運算也很復雜.下面給出這道題的其他解法.

題目已知m∈R，解關于x的不等式:

1-x≤|x-m|≤1+x.

1 考生答題反饋

解法1等價變形去絕對值符號.原不等式等價于

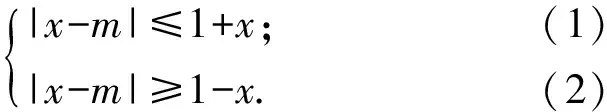
由式(1),得

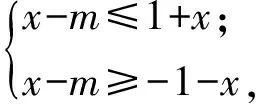
即

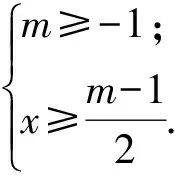
(3)

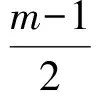
x∈φ.

(4)

由式(2),得

x-m≥1-x或x-m≤x-1,

即

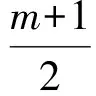
(5)

實際上,式(5)等價于當m≥1時，x∈R；當m<1時，

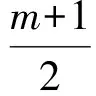
(6)

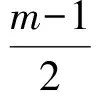
等價變形對大部分學生來說是比較簡單的，但對式(3)、式(5)的等價變形是此題的難點.絕大多數學生因為無法理解式(3)和式(5)而無法繼續完成此題.原因有2個：一是對變量參數的理解沒到位；二是沒有真正理解“且”與“或”.

解法2零點分區間討論去絕對值符號(參考答案的解法,此處略)，此法解題的困難同解法1.

2 巧妙解法

其實對于含參數的絕對值不等式，不應急于去絕對值符號.如果采用數形結合的方法，那么不僅可以大大降低難度，而且可以變抽象為直觀，有利于學生理解.

解法3利用數形結合,分別作出函數y=1-x，y=|x-m|，y=1+x的圖像，則不等式1-x≤|x-m|≤1+x表示介于直線y=1+x下方和直線y=1-x上方之間.

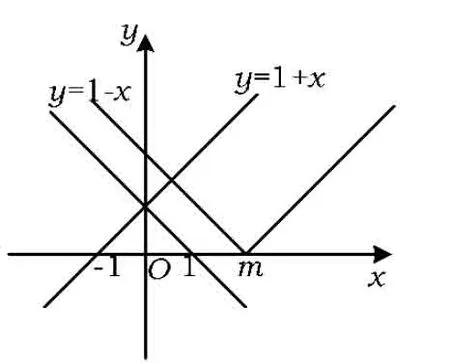
圖1

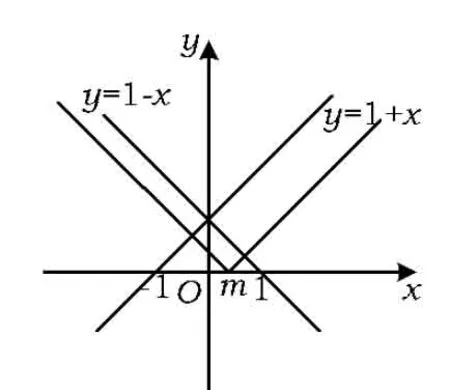
圖2

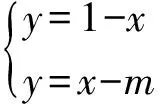
當m<-1時，不等式的解集為φ，如圖3所示.

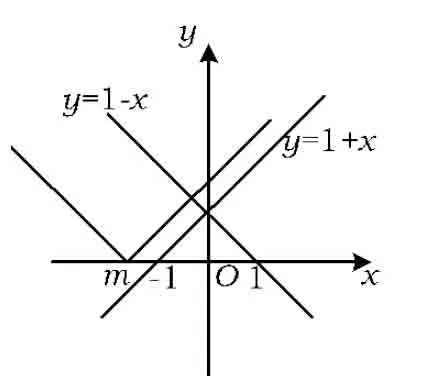
圖3

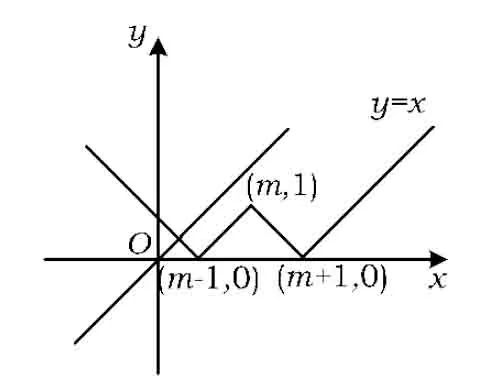
圖4

解法4利用數形結合,不等式1-x≤|x-m|≤1+x等價于

-x≤|x-m|-1≤x，

即

||x-m|-1|≤x，

于是作出函數y=||x-m|-1|和函數y=x的圖像.

當m-1≥0，即m≥1時，由

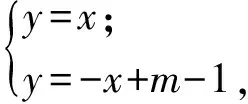
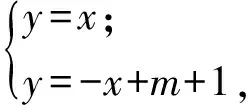
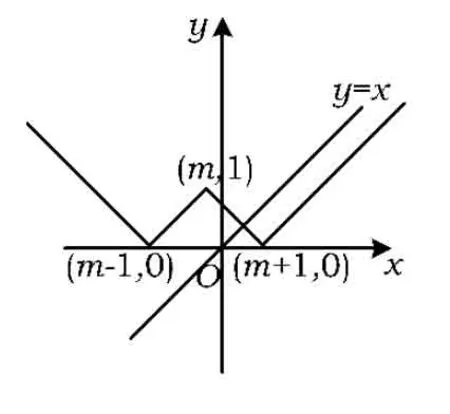
圖5

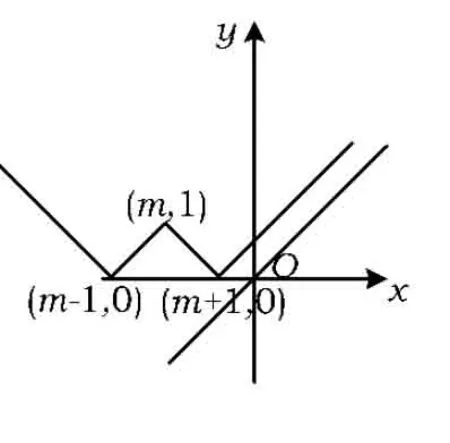
圖6

數形結合的方法其優勢是讓討論變得自然，讓分類標準明確，答案簡潔明了.其局限性是學生作圖能力差，數形結合的意識淡薄，自行處理圖像有困難.

3 教學思考與啟示

3.1 應加強學生對數學基礎知識的學習

從學生不完善的解法中可以發現，出現的問題主要是學生對一些基本概念(譬如交、并)、基本技能(數形結合)沒有掌握好.在教學中應強調對基本概念和基本思想的理解和掌握，對一些核心概念和基本思想(如函數、空間觀念、運算、數形結合、向量、導數、統計、隨機觀念、算法等)要貫穿于高中數學教學的始終，幫助學生逐步加深理解.熟練掌握一些基本技能，如重視運算、作圖、推理、處理數據以及科學計算器的使用等基本技能訓練,但應注意避免過于繁雜和技巧性過強的訓練.這些對學好數學都是非常重要的.

3.2 應加強學生對數學知識整體的認識

高中數學課程是以模塊和專題的形式呈現的.因此，在教學中應注意溝通各部分內容之間的聯系，例如，在教學中要注重函數、方程、不等式的聯系；數與形的聯系等.通過類比、聯想、知識的遷移和應用等方式，使學生體會知識之間的有機聯系，感受數學的整體性，進一步理解數學的本質，提高解決問題的能力.