簡單雙足被動行走模型仿真和分析

胡運富，朱延河，吳曉光，趙 杰

(哈爾濱工業大學 機器人研究所，哈爾濱150001，huyunfu134@yahoo.com.cn)

傳統雙足機器人的研究主要是基于ZMP 穩定判據和工業機器人軌跡跟蹤的控制方法［1］.這些機器人依賴于大力矩，高增益反饋的驅動系統以及上層的軌跡規劃和姿態平衡控制.復雜的控制和驅動系統以及過高的能量消耗限制了此類機器人的實用化.相對于傳統機器人而言，被動步行機器人以其結構和控制簡單，步態自然，節能和在非結構化環境中具有更好的移動能力等特點引起廣大學者的極大關注［2］.

Mochon 和McMahon 研究僅依靠重力下坡的機器人［3］，指出人類在行走過程中，部分依靠了重力來驅動擺動腿運動，這與雙擺很相似.在1989 年，McGeer 發現［4-5］:完全不用驅動和控制的機器人也能實現穩定的步行運動，進而提出了“被動動力步行”概念.在此之后，許多人開始對被動機器人進行了研究，Garcia［6］，Collins［7］等還對機器人行走的參數匹配問題進行了研究.近年來美國Cornell 大學［8］，MIT［9］和荷蘭的Delft 大學［10］在被動機器人研究方面成績突出［11］.被動機器人具有自然的步態和類似于人類步行的能量效率，通過研究被動步行可以更好地挖掘人類步行的本質.然而，被動機器人理論研究尚不成熟，理論模型與實際樣機差異大，且所有的分析只能建立在機器人能成功行走的基礎上.

本文以此為出發點，從被動機器人模型的建立、仿真過程和運動特點，都給出了詳細的闡述;利用數值仿真的結論，在Adams 中對實際樣機模型進行驗證，給出了從機器人建模到能行走的全過程分析;這將有助于快速理解被動機器人運動的本質，為進一步深入研究被動機器人打下基礎.

1 模型

建立的最簡單的被動行走機器人模型如圖1，由兩個剛性的直腿并通過一個被動鉸鏈聯結.該模型中的兩個直腿具有完全相同的質量和幾何參數，不同于以往研究的點足模型(點足模型與實際機器人差異很大)，該模型每條腿的質量都是均勻分布的，大小為m，其相對質心的轉動慣量均為J;腿長均為l;質心距離髖關節的距離為c;考慮到運動的穩定性，采用圓弧足，半徑為r.

圖1 簡單被動行走模型

為使仿真可行，作如下假設:

1)腿是剛性的，沒有彈性變形且髖關節為無阻尼無摩擦;

2)將足與地面的碰撞理想化，認為圓弧足不發生變形和滑動，且碰撞是瞬時的，完全非彈性碰撞，無打滑和彈起現象;

3)認為地面是剛性的、平坦的，且有小角度的斜坡.

2 動力學建模

給定初始條件，該簡單被動動力模型在重力和自身的慣性作用下，可沿小坡度的斜面穩定地向下行走.其每一步運動過程可分為如下兩部分:

1)當擺動腿離開地面時，支撐腿繞支撐足做倒立擺運動(支撐足與地面是純滾動)，而擺動腿則繞髖關節做單擺運動，準確的描述是該擺動腿繞沿著弧線軌跡運動的支點做單擺運動.此過程為連續運動階段.顯然該過程中只有重力做功，故其總的機械能是守恒的.

為使所建立的動力學方程適用性更廣，將方程無量綱化:令KJ=J/ml2，Kr=r/l，KC=c/l，且將時間無量綱化為;由拉格朗日方程推導該階段的動力學方程，可得

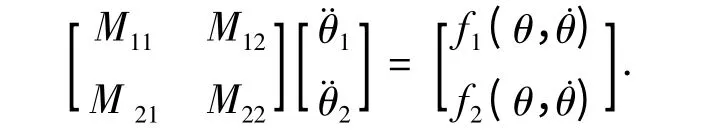
其中:

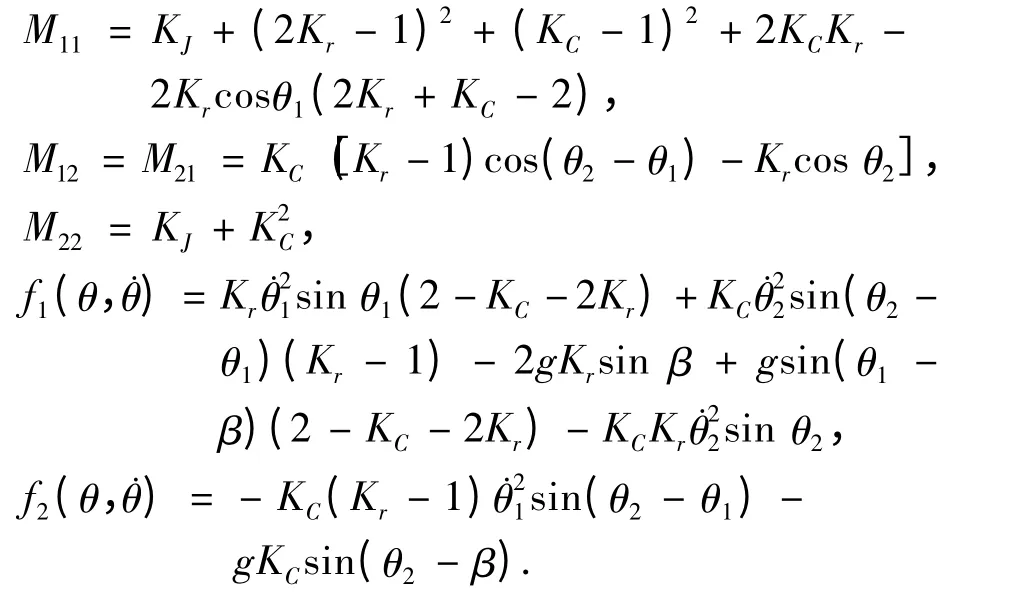
2)當擺動腿與地面碰撞后，擺動腿和支撐腿角色互換，同時碰撞是瞬時的，完全非彈性(擺動足與地面無滑動)，故在碰撞前后，兩腿角速度發生變化，而兩腿角度不變，系統滿足角動量守恒.現可基于角動量守恒方程，描述碰撞過程:設碰撞瞬間前后分別用上角標“-”和“+”表示，系統角動量用L 表示.

對于碰撞點B 和髖關節H 角動量守恒:

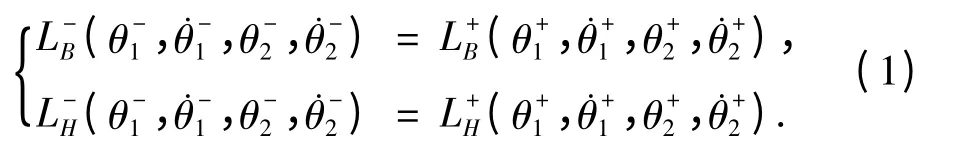
由前述分析知:

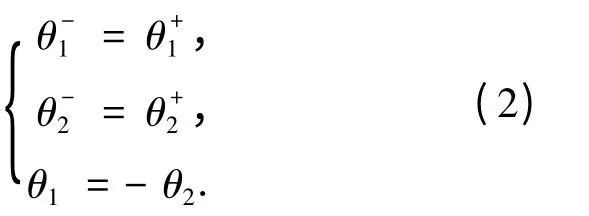
該無膝被動模型的擺動方程和碰撞方程構成了一個完整步態周期的動力學模型，為后續的仿真和穩定性分析打下基礎.

3 MATLAB 數值仿真

只要設計的模型參數合理，并且所給的初始條件恰當，該模型就能形成穩定的行走步態.現通過具體例子說明Matlab 仿真的過程.如設計的模型幾何參數如表1.

表1 每條腿的參數

非線性系統對初值極其敏感，且能控制的只是其初始條件，其以后的運動是可預知的被動運動.以機器人兩腳同時著地且碰撞發生后的瞬間為初始狀態.被動動力行走機器人對初始狀態有嚴格的要求，它應該滿足這樣的條件:機器人擺動腿的初始傾角及角速度在完成一個完整步態周期后，應具有與其上一步相同或相近的傾角和速度，從而可以實現周期性的行走運動.其初始狀態可由3 個獨立的參數來表示，即

對機器人每個完整步態包括2 次碰撞.機器人穩定行走時，在一個周期中重力所做的功ΔEP應等于這兩次碰撞造成動能的損失ΔEP.

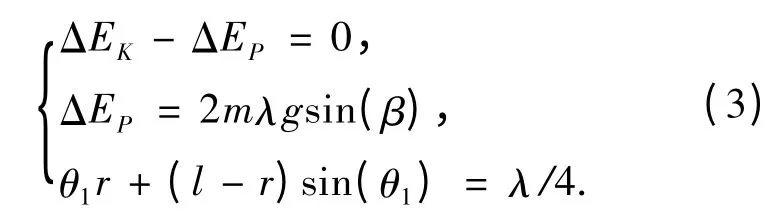
其中λ 為步長.

通常采用迭代的方法尋找能使被動行走機器人穩定行走的初值，但是迭代初值的選取帶有隨機性，合適的迭代初值很難選取.若選取不好則迭代難于收斂，無法獲得仿真初值.對于該被動行走模型的動力學方程，通過能量分析的方法，利用方程(3)尋找迭代初值范圍.在該范圍取φ01=(0.133 61，-1.390 00，-1.310 00).在Matlab 中作出仿真曲線，如圖2 所示.

圖2 中反映了該模型運動前15 步的曲線變化，實線和虛線分別對應圖1 中的腿1 和腿2.可看出該模型在經過前幾步調整后，運動逐漸穩定.上圖中的小圓圈“o”分別表示雙足同時著地時各腿所對應的角度和角速度.

從圖2(a)中可看出擺動腿的角位移變化幅度大，而支撐腿的角位移變化幅度小，雙腿重合時角位移大于零，這說明雙腿在所行走的斜面垂直位置左側重合.對于擺動腿在一個周期內的角度變化曲線可以看出:擺動腿離地時首先有個反向回擺的過程，然后向前擺動，最后回落與地面碰撞.

從圖2(b)中可看出支撐腿的角速度時刻小于擺動腿的角速度.擺動腿的角速度變化范圍比較大，從負值到正值，再減小到負值;而支撐腿的角速度始終為負值，這說明支撐腿是始終向前運動的.碰撞時兩腿速度的絕對值同時減小，故此刻機器人動能是減小的.

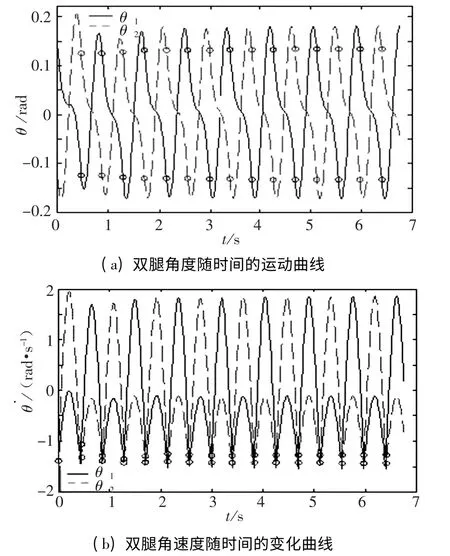
圖2 雙腿運動狀態隨時間的變化曲線

圖3(a)反映了該被動模型在所給的初始條件下，腿1 隨時間變化的相圖，每個線圈對應一個完整步態，該圖中體現了模型運動的兩個階段:A點為初始狀態，從A 到B 階段為腿1 是支撐腿階段;在B 點擺動腿(腿2)與地面碰撞造成支撐腿(腿1)角速度突變(絕對值變小)，同時支撐腿和擺動腿角色互換，故從B 到A 腿1 為擺動腿階段，在A 點腿1 與地面碰撞其角速度突變(絕對值變小)，此時兩腿角色再次互換.從圖中還可看出腿1 作為支撐腿時因擺動腿與地碰撞造成的速度損失要大于其自身作為擺動腿時與地面碰撞造成的速度損失.經過前2 圈的調整后，腿1 的狀態隨時間變化，收斂到同一個線圈中，這是后面要說的“極限環”，它反應了該機器人的行走能呈現穩定步態.

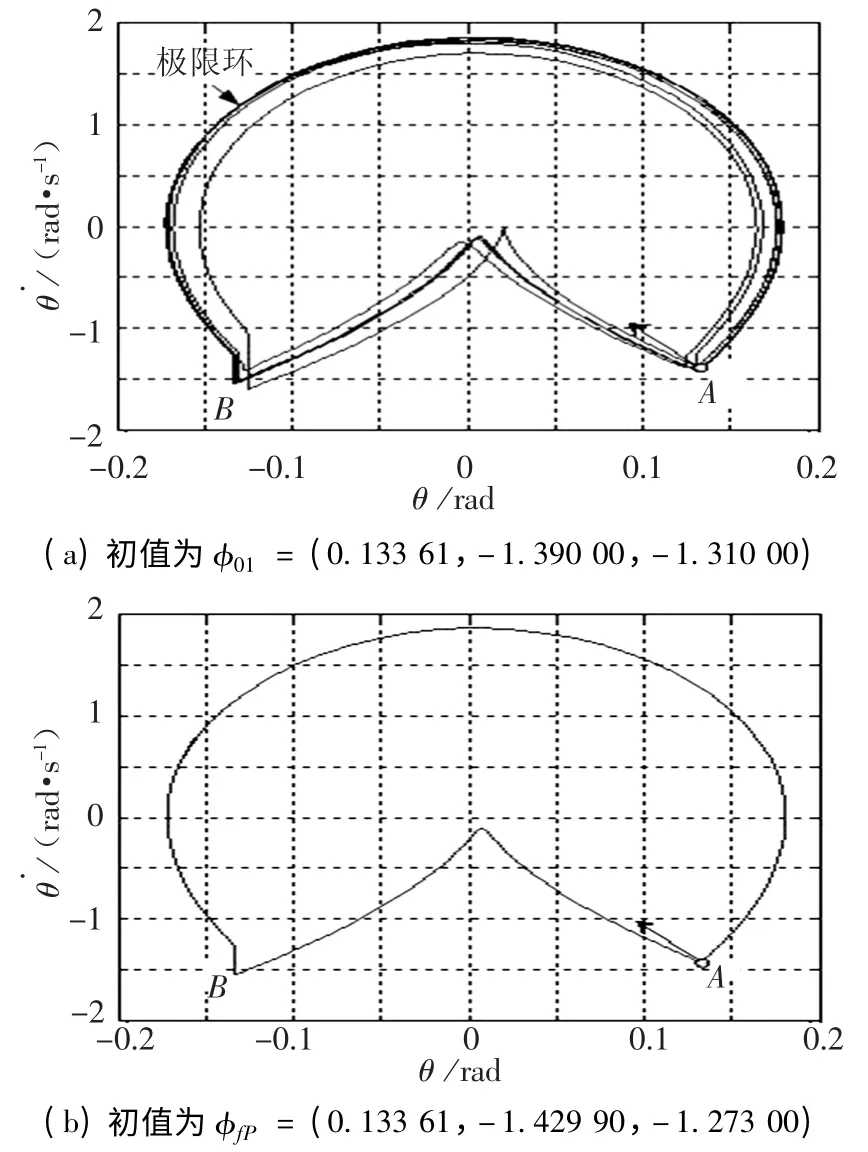
圖3 腿1 的相圖

當經過幾個步態后，如果機器人的運動在其對應的相圖中重復在一個環線上運動時，該機器人的運動就是穩定的，該環線即為“極限環”.該環線上所對應的起始點為“不動點”;如果所給的初始條件偏離不動點在一個小的范圍內，那么經過若干步后，機器人的運動相圖軌跡會回到“極限環”上，形成穩定步態.那么多小的范圍能保證運動收斂到極限環?這就需要求該不動點的吸引盆，這不在本文討論范圍內.

現考慮如何求不動點.假設“相空間”中的不動點為φfP，由于系統強的非線性，故可以用非線性函數S 來表示空間中的點

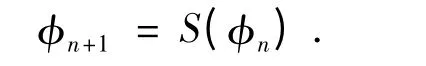
這里的S 是包括碰撞在內的一次完整的動態步行的表達式，它反映了φn+1和φn之間的關系，所有的初始條件可以寫為不動點和偏差的和:

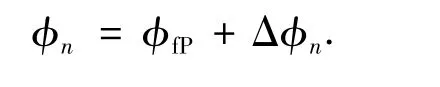
雖然S 高度非線性，但對于偏離不動點的小的偏差Δφn，仍然可用線性化的方法來估計相空間

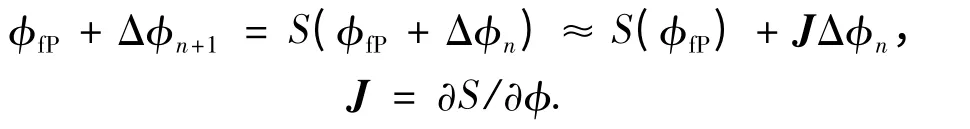
重復

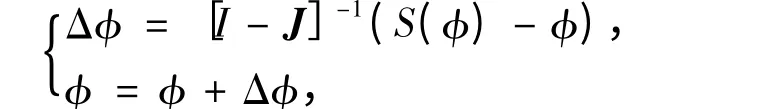
直到

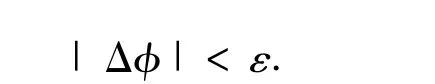
對于上面所給的初值φ01= (0.133 61，-1.390 00，-1.310 00)，求得不動點為φfP=(0.133 61，-1.429 90，-1.273 00)，將該不動點作為模型運動的初始條件，由圖3(b)知此時腿1 的相圖軌跡完全重復同一個線圈，此線圈也為腿1 所在相平面的“極限環”.

圖4 從能量的角度給出了模型在運動過程中，動能、勢能及其總的機械能的變化曲線，從圖中可以看出:在一步過程中，動能是先減小，后增大，再減小，最后再增大;而勢能的曲線變化趨勢正好相反，這說明擺動腿和支撐腿之間存在某種耦合關系.每步結束時的動能幾乎和該步開始時的動能大小一樣;每步結束時的勢能幾乎相當該步開始時的勢能的等差遞減.在每一步的擺動階段，因為只有重力做功，故總的機械能守恒;在碰撞階段，因為動能突變，而勢能不變，故總的機械能也突變(減小).在一個完整的步態周期中，重力對系統所做的功等于因碰撞損失的動能.

圖4 模型運動過程中能量變化曲線

4 Adams 仿真驗證

由于雙足被動行走機器人系統是復雜的非線性動力系統，建立其動力學數學模型時需要對機械結構參數、行走環境參數進行簡化、優化，而ADAMS 的仿真環境更逼近實際的實物試驗環境.為了驗證以上所分析的結果對以后實際物理樣機的成功行走有實際的指導意義，可將由Matlab 求出的不動點

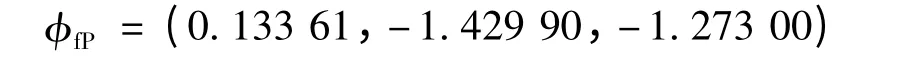
帶入Adams 的虛擬樣機中作為初始條件，來驗證分析的合理性.

根據圖1 的模型，設計出該模型相對應的實際的物理樣機造型，其可通過兩對對稱的腿做成一個“兩直腿”模型如圖5 所示.該模型的建立，解決了模型行走過程中側向平衡問題;同時圖中棋盤路面的設計，避免了運動過程中擺動腿與地面相碰的“擦地”現象.下面在Adams 中通過一些仿真曲線來分析樣機模型的運動特點.

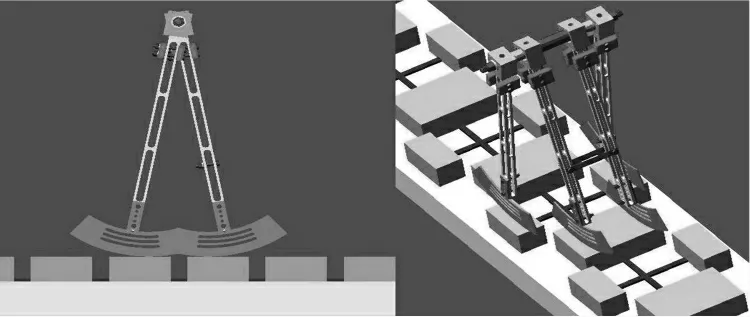
圖5 Adams 虛擬樣機仿真模型

從圖6(a)可以看出經過及其短暫的調整(幾乎不用調整)，機器人的運動很快收斂到“極限環”上，呈現穩定的周期運動.可見，通過數值仿真獲得的不動點，可作為相應的實際的樣機行走的初值條件.

從圖6(b)中可看出，在同一完整步態周期中，腿1(實線)作為擺動腿時角速度極值大于腿2(虛線)作為擺動腿時的角速度極值，可見雖然腿1 和腿2 在結構上是對稱的，但在實際的運動過程中表現出的運動形態并不對稱.

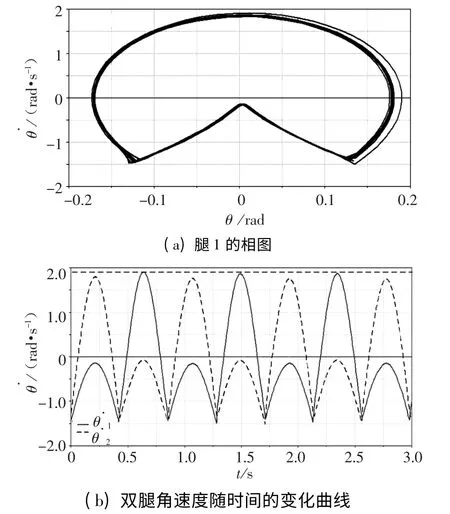
圖6 雙腿運動狀態隨時間的變化關系曲線

圖7 中實線為腿2 的足距離地面的高度，兩條虛線為兩腿運動過程中的角度曲線.當高度小于0時，說明腿2 在擺動過程中足有“擦地”現象，該現象起始于C 點，在E 點處結束，圖中D 點兩腿角度相等，即兩腿重合，可見“擦地”發生在兩腿重合之前;“擦地”現象在實際的機器人行走中是不允許的，而棋盤狀路面的運用，可避免這種現象.

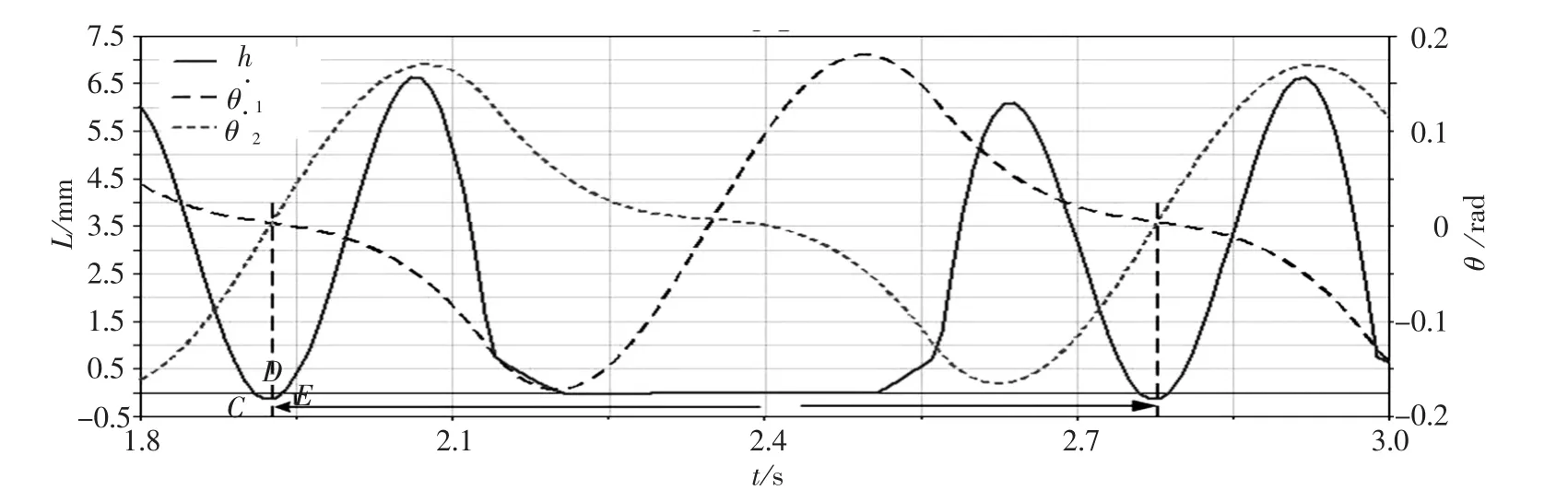
圖7 穩定行走時雙腿角度變化曲線和腿2 的足距地面高度

5 結 論

1)采用拉格朗日法建立了簡單兩桿直腿圓弧足機器人行走步態的數學模型.

2)Matlab 仿真分析并得出了理想化模型能夠行走的初值條件、運動特點和運動過程中的能量變化關系，體現了雙足機器人運動的本質特征.

3)將Matlab 仿真結果作為Adams 仿真的初始條件，獲得了更加接近真實機器人樣機穩態行走步態分析.而且在此虛擬樣機平臺上，可方便地進行參數優化和性能預測，提早發現設計問題，減少時間和經費的消耗，也可減少對物理樣機的危險操作.

4)仿真所提供的腿的長度、質量以及質心位置等參數，為最終做出物理樣機，成功在路面行走奠定了基礎.

［1］ESPIAN B，SARDAIN P.The anthropomorphic biped robot B IP2000［C］//Proceedings of the 2000 IEEE Conference on Robotics and Automation.San Francisco，CA:［s.n.］，2000:3997-4002.

［2］HUANG Q，YOKOI K，KAJITA S，et al.Planning walking pattems for a biped robot［J］.IEEE Transactions on Robotics and Automation，2001，17(3):280-289.

［3］MOCHON S，MCMAHON T A.Ballistic walking［J］.Biomechan，1980，13:49-57.

［4］MCGEER T.Passive dynamic walking［J］.International Journal of Robotics Research，1990，9(2):62-82.

［5］MCGEER T.Passive dynamic biped catalogue［C］//Proc Experiment Robotics II:The 2nd International Symposium.Berlin:Springer-Verlag，1992:465-490.

［6］GARCIA M，CHATTERJEE A，RUINA A，et al.The simplest walking model:stability，compiexity，and scaling［J］.ASME Journal of Biomechanic Engineering，1998，120(2):281-288.

［7］COLLINS S H，WISSE M，RUINA A.A 3-d passive dynamic walking robot with two legs and knees［J］.International Journal of Robotics Research，2001，20(7):607-615.

［8］COLLINS S H，RUINA A.A bipedal walking robot with efficient and human-like gait［C］//Proceedings of the IEEE Conferenceon Robotics and Automation.Piscataway，NJ，USA:IEEE，2005:1983-1988.

［9］TEDRAKE R，ZHANG T W，SEUNG H S.Stochastic policy gradient reinforcement learning on a simple 3D biped［C］//Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems.New York，NY，USA:IEEE，2004:2849-2854.

［10］SCHUITEMA E，HOBBELEN D G E，JONKER P P，et al.Using a controller based on reinforcement learning for a passive dynamic walking robot［C］//Proceedings of the IEEE/RAS International Conference on Humanoid Robots.New York，NY，USA:IEEE，2005:232-237.

［11］COLLINS S，RUINA A.Efficient bipedal robots based on passive-dynamic walker［J］.Science Magazine，2005，307:1082-1085.