采用AKF 神經網絡的直擴系統抗干擾技術

徐定杰，趙丕杰

(哈爾濱工程大學 自動化學院，哈爾濱150001，zhaopijie407@163.com)

擴頻系統除了具有保密性強、可實現碼分多址和高精度測量的優點外其抗干擾能力也很強，因此被廣泛應用于無線電及衛星導航中.它通過本地偽碼信號與接收信號進行相關得到的擴頻增益來抑制干擾信號［1］，具有一定的抗干擾能力，但由于實際信號發射功率限制及作用距離上的衰減，接收到的擴頻信號功率非常低，在強干擾條件下，尤其在有意的敵對干擾條件下，干擾強度很容易超出其干擾容限，擴頻系統便不能正常工作，這就需要采取其它技術措施增強擴頻系統的抗干擾能力.

針對擴頻系統時域上的抗窄帶干擾技術，人們進行了很多的研究并提出相應的解決方案.文獻［2］中給出了一種線性自適應最小均方差(LMS)干擾預測器，這種線性干擾預測器將引入一定誤差，因此需要一種非線性干擾預測器.文獻［3］中給出了一種非線性自適應近似條件均值(ACM)干擾預測器，它需要已知擴頻信號的數量等信息，從而得到擴頻信號與環境噪聲的聯合概率密度分布，然后得出其非線性關系.但在實際環境中，擴頻信號的數量是未知的，因此很難得到準確的非線性預測函數.文獻［4］和［5］中給出了一種基于遞歸神經網絡(RNN)的非線性干擾預測器，當擴頻信號的數量未知時，它能夠有效地改善干噪比.但它采用的實時遞推學習(RTRL)權值修改算法是基于一階微分統計量的，因此收斂速度慢，對快時變干擾信號很難準確跟蹤.

本文提出了一種基于自適應卡爾曼濾波(AKF)的遞歸神經網絡預測器(RNNP)來消除窄帶干擾.它采用一種強有力的非線性工具—全連結神經網絡［6-7］來預測干擾信號，然后運用適合于非線性系統的AKF 來反饋修改權值，克服了經典卡爾曼濾波需要精確已知系統的數學模型和噪聲統計的缺點和局限性.

文中給出了抗干擾擴頻系統的結構框圖，并詳細描述了RNNP，然后給出了基于漸消記憶指數加權的AKF 權值修改算法的遞推公式，最后對基于AKF 學習算法的RNNP 相對于常規抗干擾技術的性能進行了計算機仿真.

1 抗窄帶干擾擴頻系統

圖1 給出了抗窄帶干擾擴頻系統的簡化結構框圖.它采用相關前抗干擾模式，主要由RNNP 和一個加法器組成，通過這個干擾消除模塊可以對混雜在接收擴頻信號中的窄帶干擾信號進行估計并消除［8］.

圖1 相關前干擾抑制擴頻系統結構圖

設接收信號可以表示為

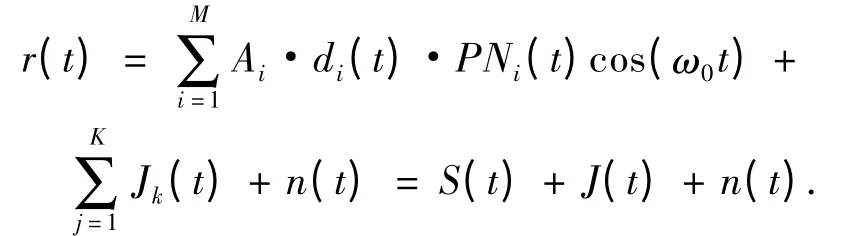
其中Ai為第i 路擴頻信號的幅值;di(t)為第i 路二進制數據信息;PNi(t)為第i 路擴頻序列，其碼片速率遠遠大于數據信息速率;ω0=2πf0為調制載波角頻率;S(t)由M 路擴頻信號組成;n(t)為加性高斯白噪聲，其均值為零，方差為σ2;干擾信號Jk(t)是指窄帶干擾，它的主要來源為接收機附近的雷達及其它射頻發射裝置發射的強功率信號或敵方針對本擴頻系統載波頻率而發射的頻率在中心頻率ω0附近的壓迫式干擾，可分為三種形式:音頻干擾、自回歸(AR)干擾和低速率數字干擾.

接收信號r(t)經過帶通濾波器、AGC 固定增益放大、下變頻及低通濾波器后，以采樣速率fs=1/Ts進行采樣，得到的第k 時刻的采樣信號為

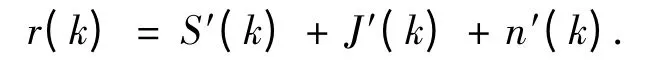
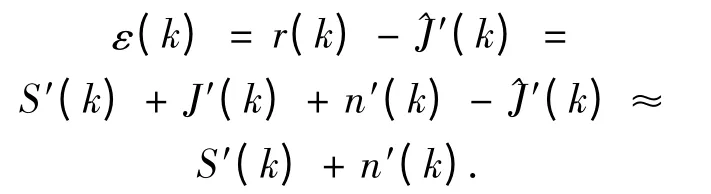
2 基于AKF 的遞歸神經網絡

2.1 遞歸神經網絡預測器

圖2 給出了遞歸神經網絡預測器(RNNP)的詳細結構，這個模塊是一種全連結的神經網絡，它由P 個外部輸入層神經元、N 個隱層神經元及一個輸出層神經元組成.與前向神經網絡不同，每個隱層神經元都延遲一個采樣周期反饋到輸入層，輸入層除了P+N 個節點外，還有固定值為+1 的偏值輸入.

RNNP 的非線性狀態方程及線性觀測方程可以表示為

圖2 遞歸神經網絡預測器(RNNP)結構框圖

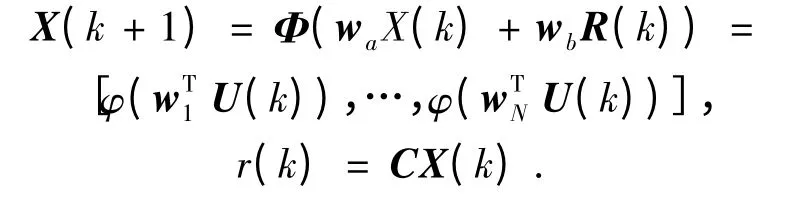
其中

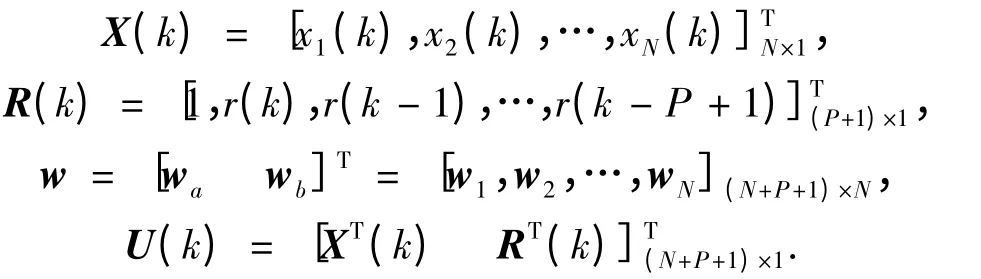
其中:wa為隱層反饋到輸入層節點的權值，wb外部輸入信號節點的權值，C 為輸出層輸入輸出線性權值系數，X(k)為RNNP 的狀態向量，R(k)為外部輸入向量，所以總的輸入層向量為U(k).輸入層的輸入輸出關系采用直接賦值的方式.

輸出層的輸入為隱層的輸出，輸出y(k)為輸入的線性組合，即其值為RNNP 預測的干擾信號.

2.2 基于漸消記憶指數加權的AKF 學習算法

根據上面神經網絡模型可以得到隱層反饋到輸入層權值W(k)的線性狀態方程和非線性觀測方程為

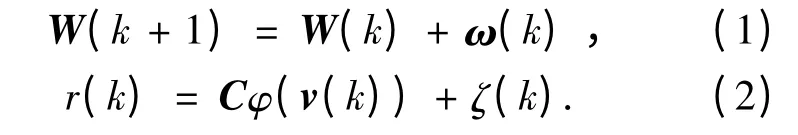
為解決式(2)中非線性觀測方程的估值問題，常用的方法是擴展 Kalman 濾波器(EKF)［9-10］，它的缺點和局限性有兩點，一是它要求已知狀態和觀測噪聲統計特性，然而實際應用問題中噪聲統計特性卻常常是近似的、時變的.運用不準確或錯誤的噪聲統計特性設計EKF 將使濾波器性能變壞，甚至使濾波發散.二是EKF的基本原理是將非線性系統線性化，然后用線性化常規Kalman 濾波器解決非線性系統狀態估值問題，其中忽略了非線性化引入的模型誤差，將導致濾波性能變差.為了解決上述問題，本文采用基于漸消記憶指數加權的AKF 學習算法來修改遞歸神經網絡的權值系數，其原理為:在進行狀態濾波的同時，利用觀測數據提供的信息，在線估計未知噪聲統計特性，構成狀態和噪聲統計特性估計的兩段互耦自適應卡爾曼濾波算法.Sage 和Husa的噪聲統計估值器可在線互耦估計狀態和噪聲統計，算法簡單且具有良好的性能，因此被人們廣泛應用.它由互耦的常規卡爾曼濾波算法和噪聲統計估值器組成.Sage 和Husa 的噪聲統計估值器是次優無偏極大后驗估值器，適合估計未知的噪聲統計，其缺點是不能處理時變噪聲統計估計問題，且精度有待于進一步提高.本文引入基于漸消記憶指數加權的改進的Sage 和Husa 噪聲估值器，它可處理時變噪聲統計估值問題，且計算效率高，能加快收斂速度，提高算法的跟蹤性能，使得濾波過程穩定、可靠、精度高.

由于噪聲的統計特性未知，將式(2)中的φ在W(k)的預測值)處用泰勒級數展開有

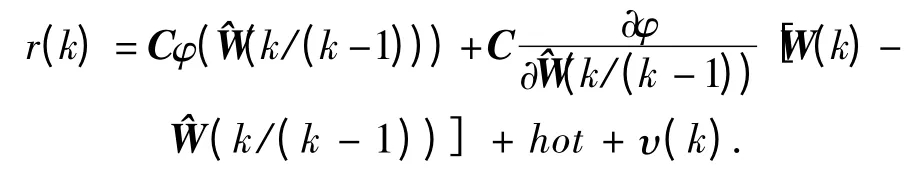
這里引出線性化觀測方程

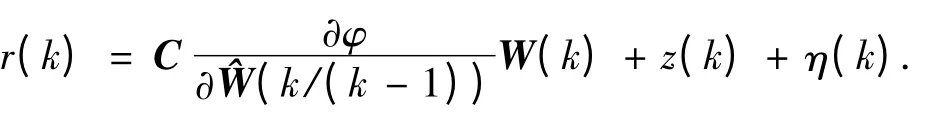
其中

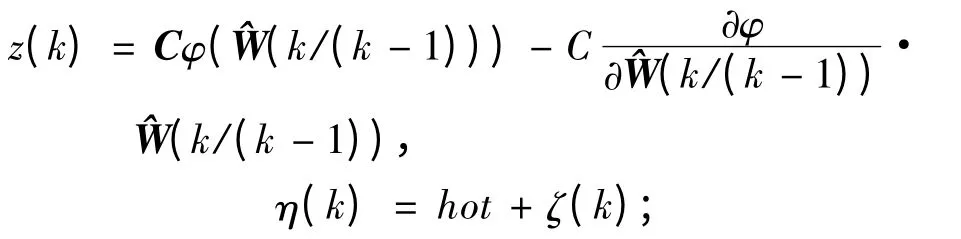
其中:hot 為泰勒級數展開的高階項;η(k)為虛擬觀測噪聲，用以補償線性化誤差hot，它的時變統計特性為

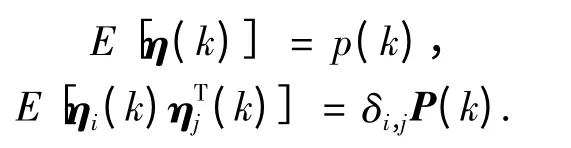
設隱層輸出矩陣φ(v(k))關于權值W(k)的偏微分矩陣為Ω(k)，它是N×L 階矩陣，可以表示為

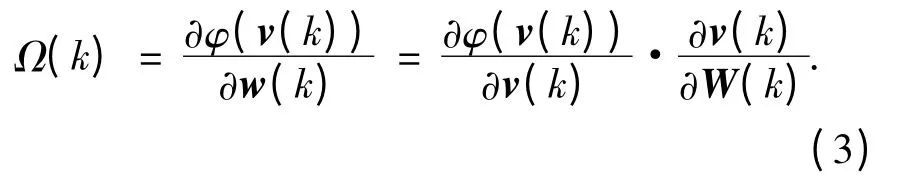
其中

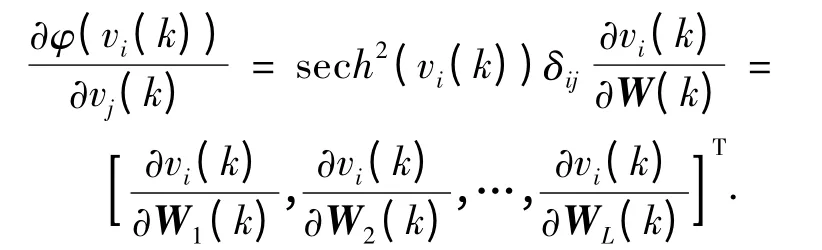
因此帶未知噪聲統計的非線性方程(1)和(2)的自適應卡爾曼濾波狀態一步預測的遞推公式為

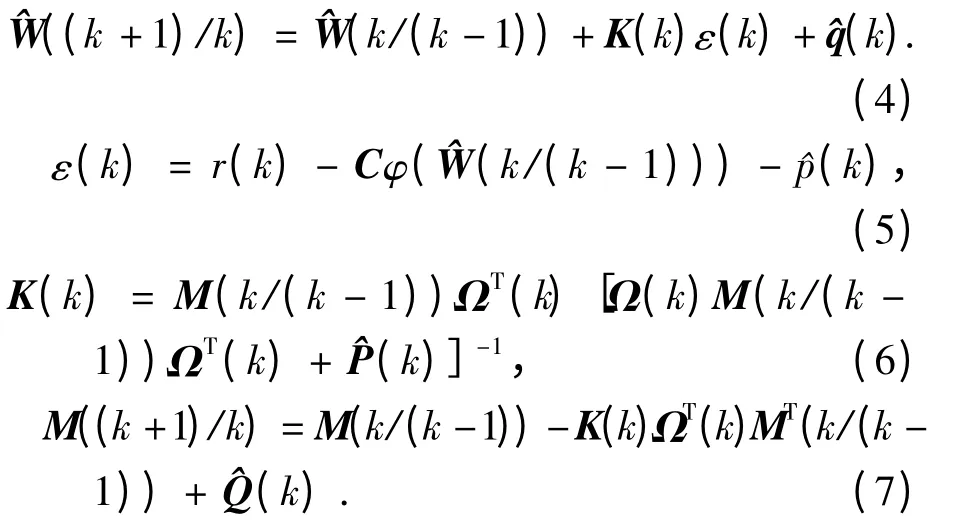
其中Ω(k)由式(3)定義，基于漸消記憶指數加權的噪聲統計特性估值器為

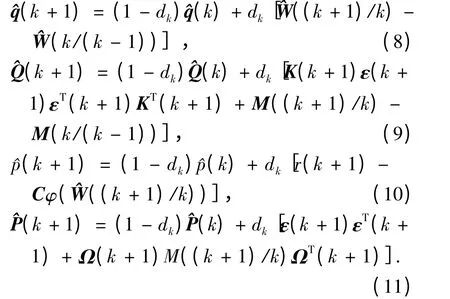
其中:

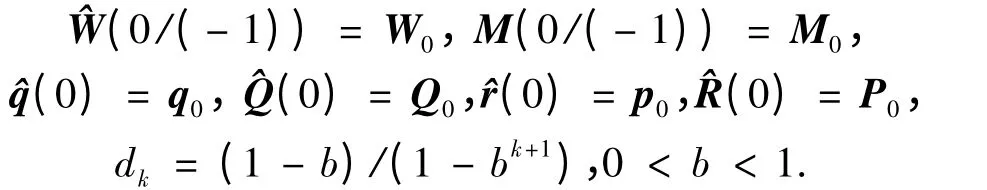
式中:b 為遺忘因子，其取值范圍一般b ∈(0.95 ～1)，對于慢時變噪聲b 取值較大，接近于1.則狀態噪聲統計估值的兩段互耦自適應Kalman 濾波學習算法的程序流程為

步驟1 初始化權值向量W0，誤差協方差矩陣M0，噪聲統計估值q0，Q0，p0和P0;

步驟2 根據式(4)和式(5)計算k 時刻預測誤差ε(k)和濾波增益矩陣K(k);

步驟3 根據式(6)和式(7)更新k+1 時刻的權值預測值和誤差協方差矩陣M((k+1)/k);

步驟4 根據式(8)～(11)更新k+1 時刻時變噪聲統計估計值，

步驟5 時刻k 遞增準備下一時刻的窄帶干擾預測抑制.

3 仿真結果

為了比較基于AKF 學習算法的RNNP 相對于自適應線性LMS 干擾預測器、自適應ACM 干擾預測器和基于RTRL 算法的RNNP 的抗干擾性能，進行了計算機仿真.首先，介紹輸入信號的組成;其次，介紹衡量抗干擾性能的標準;最后，給出各種抗干擾技術的性能比較.

3.1 輸入信號組成

仿真中的輸入有用擴頻序列采用15 級m 序列，環境噪聲是方差為0.1 的加性高斯白噪聲，干擾信號只考慮下面兩種形式:

1)單頻連續載波干擾(CWI).它是一種最為常見的干擾信號，例如射頻干擾，CWI 時域上的數學表達式為j(k)=2sin(0.01k);

2)自回歸干擾(ARI).它是由高斯白噪聲遞推產生的隨機信號，其時域上的數學表達式為

j(k)=1.980 0j(k-1)-0.980 1j(k-2)+n0(k).其中n0(k)是方差為0.01 的高斯白噪聲.

3.2 抗干擾性能標準

為了對各種預測器的抗干擾性能進行比較，主要參考下面兩個性能指標:干噪比(JNR)改善量和信噪比(SNR)損失量，它們可以表示為

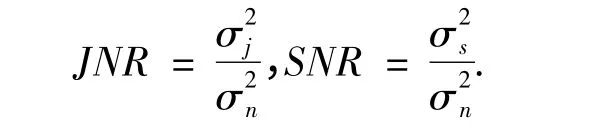
圖3 仿真中SNR 和JNR 的計算方式

在上面仿真中，擴頻信號與噪聲及干擾與噪聲的互相關很小，接近于零，可以忽略.所以信號+噪聲與信號的互相關值表示信號的能量，干擾+噪聲與干擾的互相關值表示干擾的能量，信號+噪聲及干擾+噪聲與噪聲的互相關值都表示噪聲的能量，所以通過圖3 可以計算窄帶干擾抑制技術的JNR 改善量和SNR 損失量，表示為

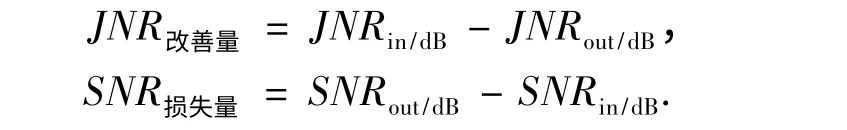
3.3 仿真結果與性能分析

RNNP 中輸入層節點個數為4，隱層節點個數為5，輸出層節點個數為1，輸出層輸入輸出線性權值系數C=［1，1，1，1，1］，權值初始值為零，初始誤差協方差矩陣為100E，其中E 為單位矩陣，噪聲統計初始估計值為零或單位矩陣.圖4 和圖5 給出了當干擾分別為頻率500 Hz 的CWI 和低頻段的ARI 時，基于AKF 學習算法的RNNP 干擾抑制前后的信號的頻譜圖.可以看到，基于AKF學習算法的RNNP 能準確估計并消除混雜在接收信號中的強窄帶干擾信號.

圖6 和圖7 給出了當干擾分別為CWI 和ARI時，基于AKF 學習算法的RNNP 干擾抑制前后的信號的偽碼相關特性.可以看到，強窄帶干擾存在時，偽碼相關特性不再滿足理想的相關特性，導致接收機無法正常工作，而基于AKF 學習算法的RNNP 能很大程度的抑制干擾信號，并且對有用擴頻信號的損傷比較小，經過干擾抑制后，可以明顯地在偽碼相關曲線中碼片延遲為511 chip 時發現相關峰值，使得接收機能夠在強窄帶干擾環境下正常捕獲和跟蹤擴頻信號.

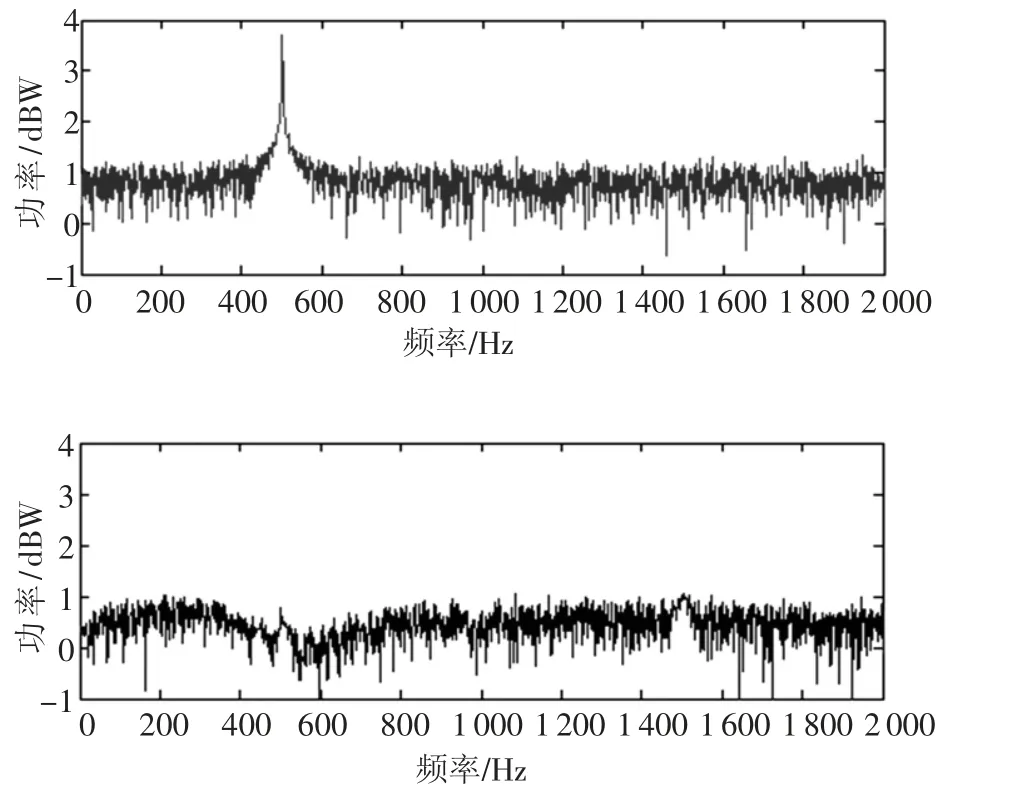
圖4 CWI 及其干擾抑制前后效果

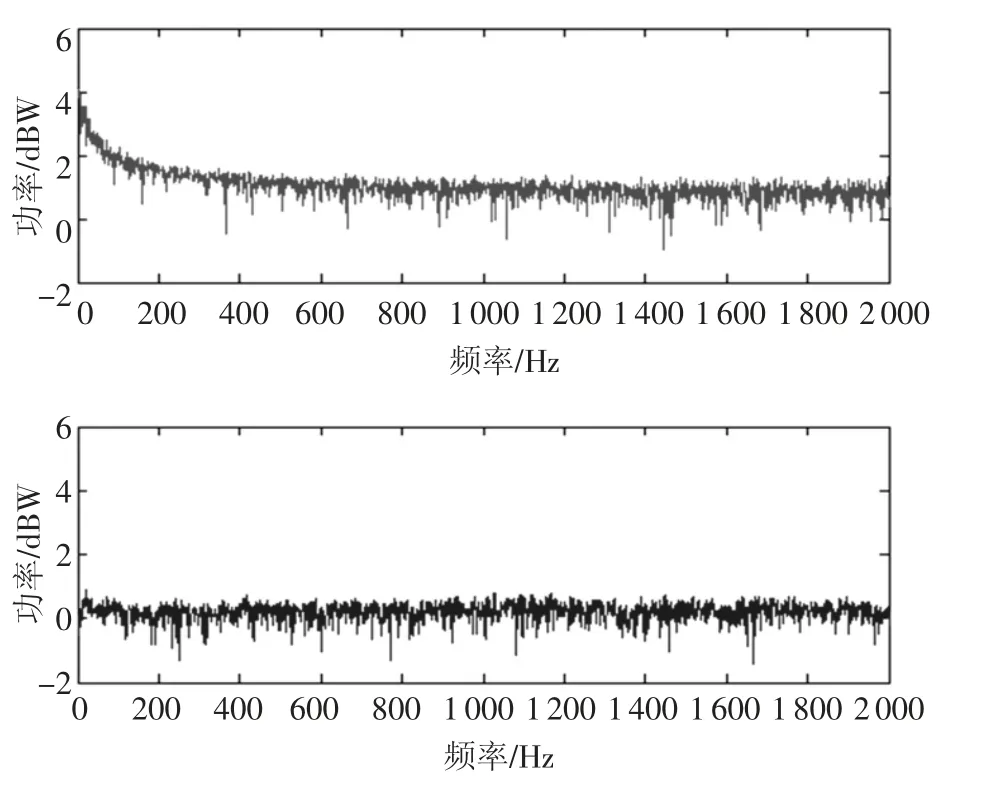
圖5 ARI 及其干擾抑制前后效果

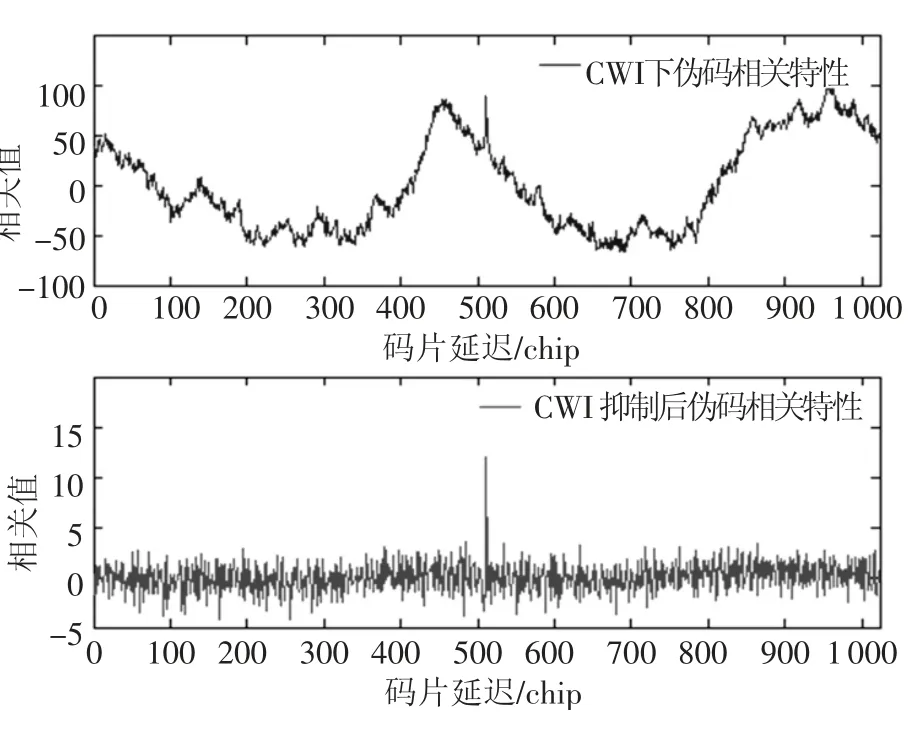
圖6 CWI 抑制前后偽碼相關特性

圖7 ARI 抑制前后偽碼相關特性

圖8 和圖9 給出了當干擾分別為CWI 和ARI時，基于AKF 學習算法的RNNP 誤差輸出的均方誤差曲線.可以看到:1)基于AKF 學習算法的RNNP 的窄帶干擾預測誤差比其它干擾抑制技術要小的多，說明其干擾預測精度更高;2)基于AKF 學習算法的RNNP 的窄帶干擾預測誤差的收斂速度很快，可以實時地預測并抑制窄帶干擾信號，大大改善了其它時域干擾預測抑制算法收斂速度慢和實時性差等缺點，可以適應于快時變干擾信道.

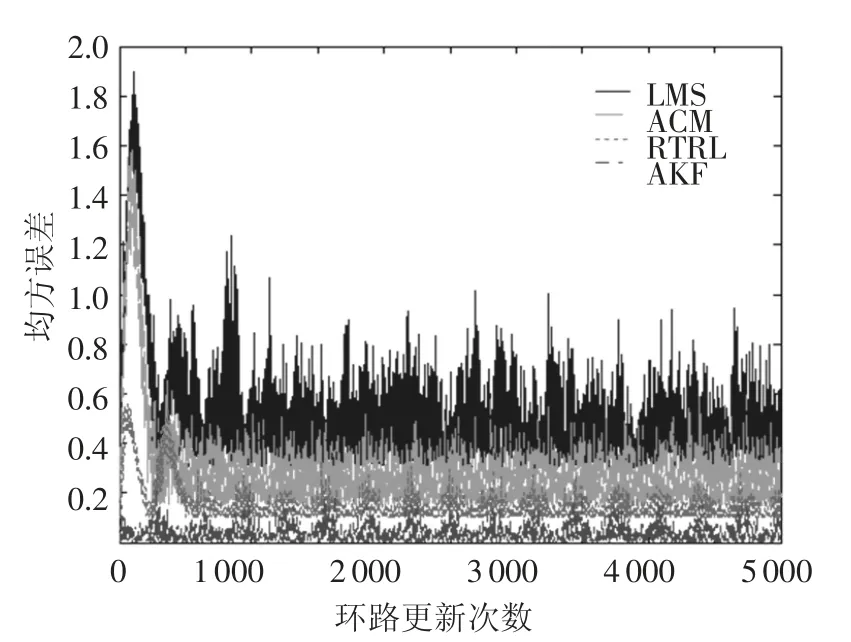
圖8 CWI 抑制后的均方誤差曲線

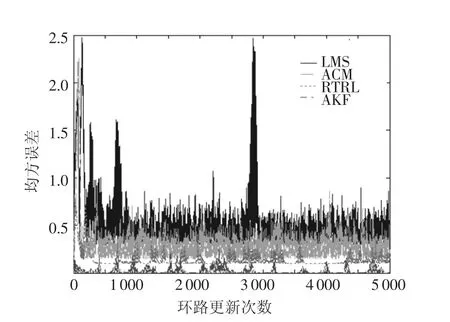
圖9 ARI 抑制后的均方誤差曲線

表1 和表2 給出了當干擾分別為CWI、ARI時，基于AKF 學習算法的RNNP 相對于其它干擾抑制技術的抗窄帶干擾性能比較.其中自適應線性LMS 干擾預測器中延遲節點的個數為5，采用最小均方差(LMS)來反饋修改權值，收斂系數為0.000 1.自適應ACM 預測器中延遲節點個數為5，采用非線性近似條件均值(ACM)來反饋修改權值，初始收斂系數為0.001，初始估計方差為1，遺忘因子為0.9.基于RTRL 算法的RNNP 與AFK 算法的遞歸神經網絡相同，權值初始值為零，初始誤差協方差矩陣為100E，其中E 為單位矩陣.輸入信噪比固定為-10 dB，輸入干噪比是變化的，可以通過改變單頻干擾信號幅值或改變噪聲n0(k)的方差來改變干擾信號的能量.可以看到:1)當干擾為CWI 時，基于AKF 學習算法的RNNP 在干噪比改善量上相對于自適應LMS、ACM 和 RTRL 干擾抑制技術分別平均有15.4 dB，14.5 dB 和8.9 dB 的改善，而對于ARI干擾，分別有13.5 dB，12.2 dB 和6.2 dB 的改善.輸入干噪比越大，干噪比改善量越大.2)當干擾為CWI 時，基于AKF 學習算法的RNNP 在信噪比損失量上比其它干擾抑制技術分別平均減少2.3 dB，1.4 dB 和0.7 dB，而對于ARI 干擾，分別平均減少2.6 dB，1.4 dB 和0.5 dB.輸入干噪比越大，對有用信號的損傷越大.

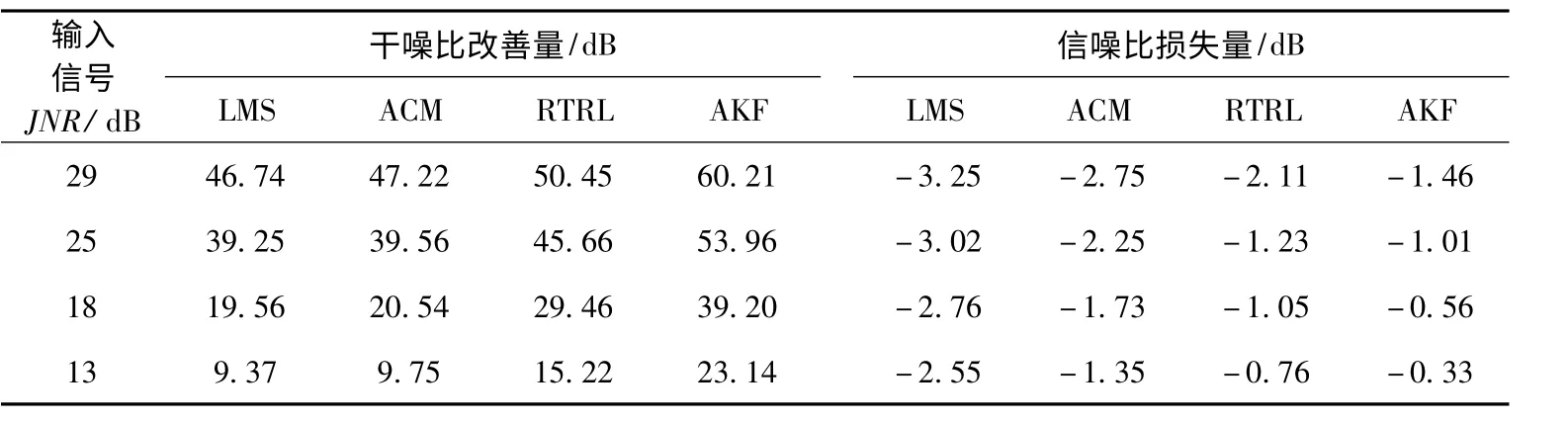
表1 CWI 下干噪比提高量和信噪比損失量

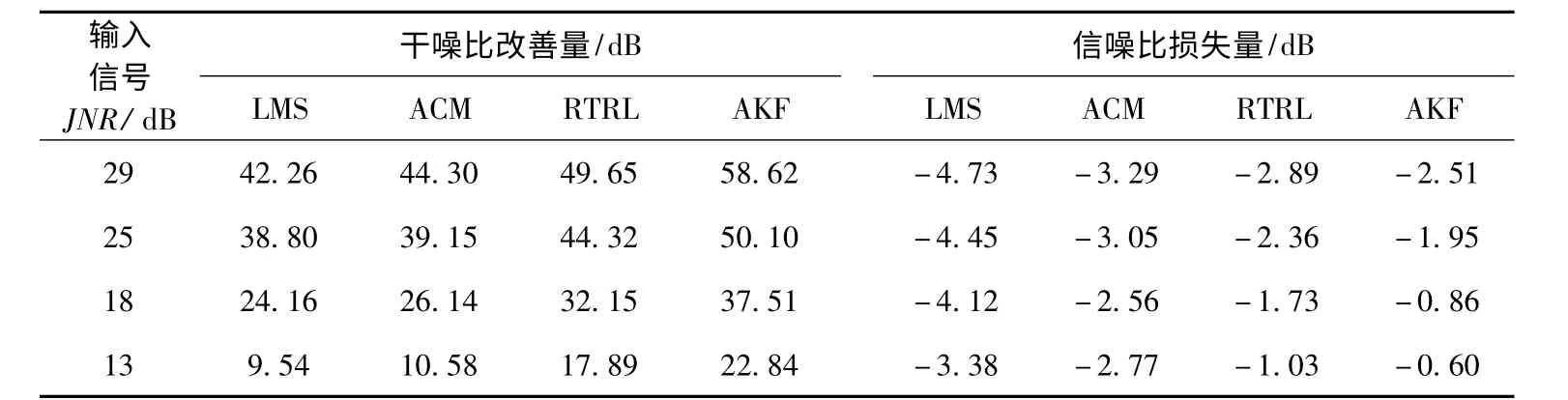
表2 ARI 下干噪比提高量和信噪比損失量

4 結 論

本文將基于漸消記憶指數加權的自適應卡爾曼濾波應用于遞歸神經網絡的學習算法中，從而準確地預測并抑制擴頻系統中的窄帶干擾.該方法不需要已知信道參數，能夠準確地預測窄帶干擾信號，并且收斂速度相對于基于自適應LMS、ACM 算法和基于RTRL 算法的RNNP 的干擾抑制技術大大提高.仿真試驗表明:當干擾信號為單頻連續載波干擾(CWI)和自回歸干擾(ARI)時，它的干噪比改善量和信噪比損失量相對于其它干擾抑制技術有不同程度的改善.

［1］PARKINSON B W，SPILKER J J.Global Positioning System:Theory and Applications:Volume I［M］.Reston:American Institute of Aeronautics and Astronautics，1996.

［2］ILTIS R A，MILSTEIN L B.An approximate statistical analysis of the widrow LMS algorithm with application to narrow-band interference rejection［J］.IEEE Transactions on Communications，1985，COM-33:10-19.

［3］VIJAYAN R，POOR H V.Nonlinear techniques for interference suppression in spread-spectrum systems［J］.IEEE Transactions on Communications，2004，38(7):1060-1065.

［4］CHANG Po-Rong，HU Jen-Tsung.Narrow-band interference suppression in spread-spectrum CDMA communications using pipelined recurrent neural networks［J］.IEEE Transactions on Vehicular Technology，1999，48(2):467-477.

［5］CHOI J，BOUCHARD M，YEAP T H.Decision feedback recurrent neural equalization with fast convergence rate［J］.IEEE Transactions on Neural Networks，2005，16(3):699-708.

［6］胡德文，王正志，王耀南，等.神經網絡自適應控制［M］.長沙:國防科技大學出版社，2005.

［7］PARISI R，DI CLAUDIO E D，ORLANDI G，et al.Fast adaptive digital equalization by recurrent neural networks［J］.IEEE Transactions on Signal Processing，2007，45(7):2731-2739.

［8］MAO Wei-Lung.Novel SREKF-based recurrent neural predictor for narrowband/FM interference rejection in GPS［J］.International Journal of Electronics and Communications，2008，62(3):216-222.

［9］謝勝利，何昭水，高鷹.信號處理的自適應理論［M］.北京:科學出版社，2006.

［10］Steven M Kay.統計信號處理基礎—估計與檢測理論［M］.北京:電子工業出版社，2003.