矩陣多項式的綜合除法及其應用

謝澤嘉

（華南師范大學數學科學學院，廣東廣州510631）

矩陣多項式的綜合除法及其應用

謝澤嘉

（華南師范大學數學科學學院，廣東廣州510631）

給出矩陣多項式的綜合除法，利用微分代數的觀點，將其應用于一類常系數偏微分方程化為無窮維Hamilton系統的問題中.再結合標準型算法，將其應用于構造一類偏微分方程組通解的問題中.

無窮維Hamilton系統；帶余除法；綜合除法；矩陣多項式；偏微分方程組通解

0 引言

求微分方程（組）的等價無窮維Hamilton系統是分析力學的反問題，是經典力學的主要問題之一.阿拉坦倉[1]提出了矩陣多元多項式帶余除法的理論，并將其應用于解決常系數偏微分方程（組）的無窮維Hamilton系統的反問題.陸斌及張鴻慶[2]將矩陣多元多項式帶余除法與標準型算法相結合，獲得構造一類偏微分方程組通解的新方法.關于矩陣多元多項式帶余除法的計算，侯國林和阿拉坦倉[3]利用Mathematica系統將文獻［1］中的結果編制成矩陣多元多項式帶余除法軟件包，用于求商式與余式.本文將類比多項式的綜合除法，給出矩陣多項式的綜合除法，以解決常系數偏微分方程（組）的無窮維Hamilton系統的反問題和構造偏微分方程組通解中所涉及的矩陣多項式的帶余除法問題.

1 矩陣多項式的帶余除法

若m×n矩陣（m、n均為正整數）A（s）的每個元素都是關于s的多項式，則稱A（s）為m×n階矩陣多項式.

若矩陣多項式的次數?[A（s）]=k（其中k為正整數），則A（s）可表示為A（s）＝A0sk＋A1sk－1＋…＋Ak，其中A0，A1，…，Ak稱為A（s）按總冪次展開的系數矩陣.其它關于A（s）的按行（列）冪次展開及按指定行（列）冪次展開的情況可參考相關文獻[4].

文獻給出了當除式為方陣時的帶余除法[5]，本文將帶余除法推廣到除式為矩形陣的情況，證明從略.以下r、l、m均為正整數，Rr×l[s]表示r×l的實系數矩陣多項式環.

左除設A（s）∈Rr×l[s]為行正則，B（s）∈Rr×m[s]，?[B（s）]≥?[A（s）]，則存在唯一的商式Q（s）∈Rl×m[s]和余式R（s）∈Rr×m[s]，使得：

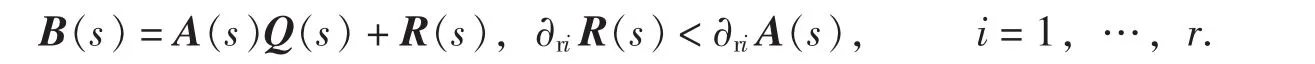
其中，?riA（s）表示A（s）第i行的次數.

右除設A（s）∈Rl×r[s]為列正則，B（s）∈Rm×r[s]，?[B（s）]≥?[A（s）]，則存在唯一的商式（s）∈Rm×l[s]和余式（s）∈Rm×r[s]，使得：

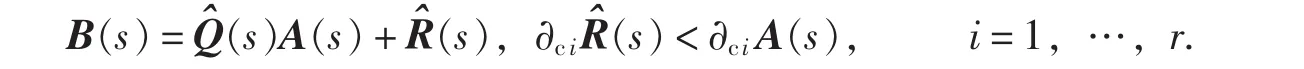
其中，?ciA（s）表示A（s）第i列的次數.

對于上面矩陣多項式的帶余除法，在具體求商與余時，左除時A（s）必須是按行冪次展開，并要求展開后的首項系數陣行滿秩，B（s）則必須是按與A（s）行冪次相同的指定行冪次展開；右除時A（s）必須是按列冪次展開，并要求展開后的首項系數陣列滿秩，B（s）則必須是按與A（s）列冪次相同的指定列冪次展開.另外，若A（s）按總冪次展開時的首項系數陣為行（列）滿秩矩陣，則同樣有類似于上面的關于按總冪次展開的左除（右除），并且被除式也是按總冪次展開.

2 矩陣多項式的綜合除法

矩陣多項式也有類似于多項式的綜合除法，當被除式與除式行數相同時可以進行左除，列數相同時可以進行右除.下面給出除式和被除式按總冪次展開的情況.

對于A（s）∈Rr×l[s]左除B（s）∈Rr×m[s]的情況（?[A（s）]=k，?[B（s）]=h，h＞k，h、k均為正整數），由矩陣多項式的帶余除法，可令B（s）=A（s）Q（s）+R（s），其中，Q（s）=Q0sh-k+

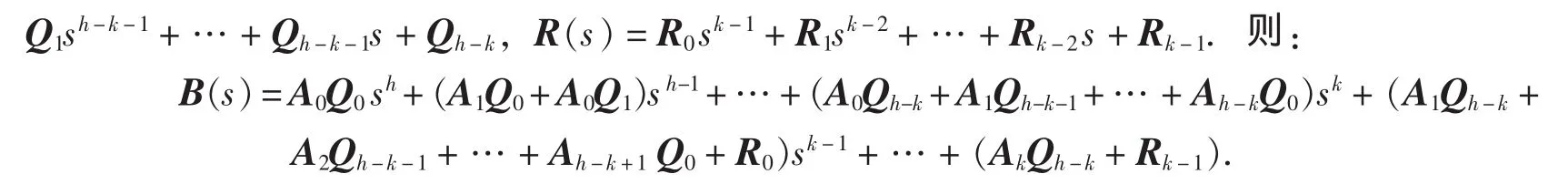
由矩陣多項式恒等可得：

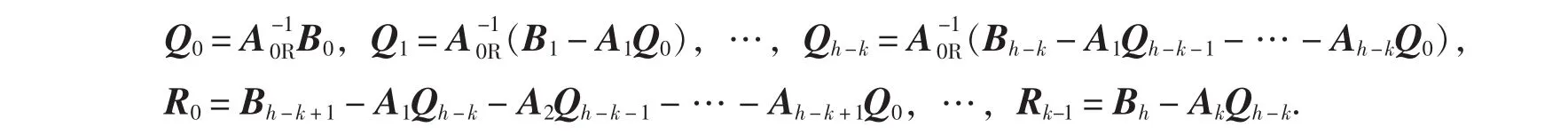
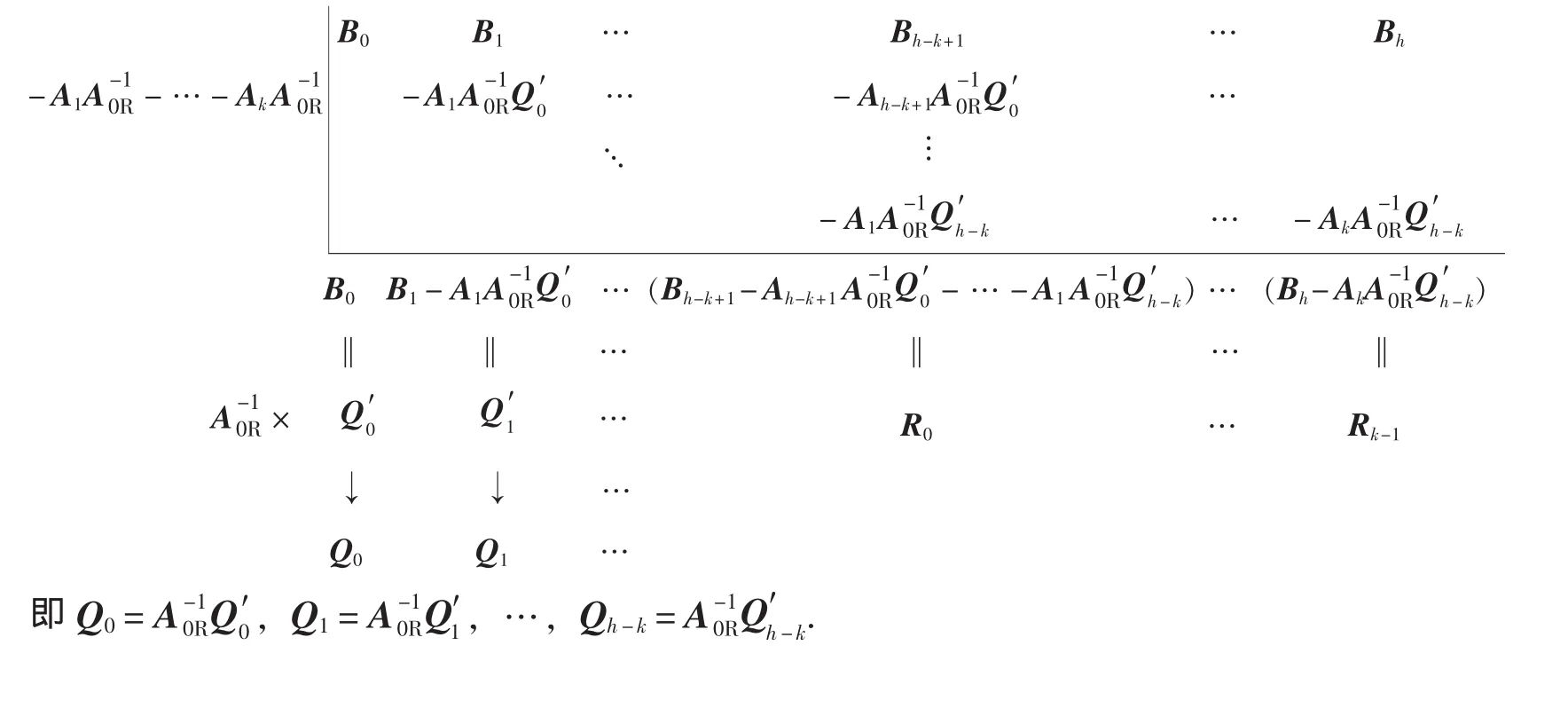
對于A（s）∈Rl×r[s]右除B（s）∈Rm×r[s]的情況（?[A（s）]=k，?[B（s）]=h，h＞k，h、k均為正整數），同理，由矩陣多項式的帶余除法，可令B（s）=Q^（s）A（s）+R^（s），其中，

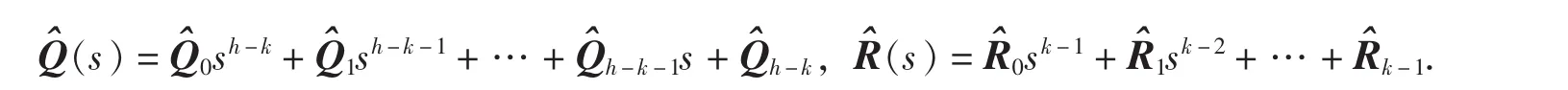
同理可得：

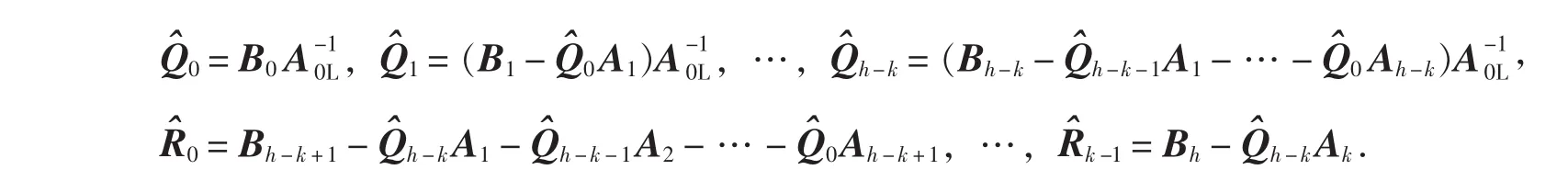
注：上面作左除和右除時，矩陣多項式的綜合除法的表示形式是不同的.對于左除，形式是“?”，而對于右除，形式則是“」”.這樣表示的原因是矩陣的乘法一般是不可交換的.

綜合除法左除按行冪次展開的情況與右除按列冪次展開的情況，分別與左除和右除按總冪次展開的情況類似.

另外，在利用矩陣多項式的綜合除法求左（右）除的商式和余式時，首先判斷除式按總冪次展開的首項系數陣是否行（列）滿秩，若是則進行綜合除法，否則再判斷除式按行（列）冪次展開的首項系數陣是否行（列）滿秩，是則進行綜合除法，否則不能.

3 矩陣多項式綜合除法的應用

3.1 在無窮維Hamilton系統中的應用

關于無窮維Hamilton系統的相關概念可參考阿拉坦倉教授的文獻[6].

解該偏微分方程可寫為多元多項式：

其中關于x的次數為2.故無窮維Hamilton系統的矩陣多元多項式為

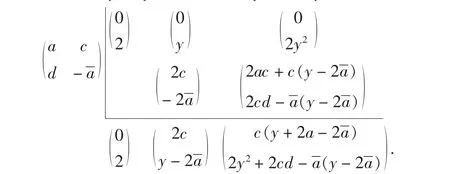
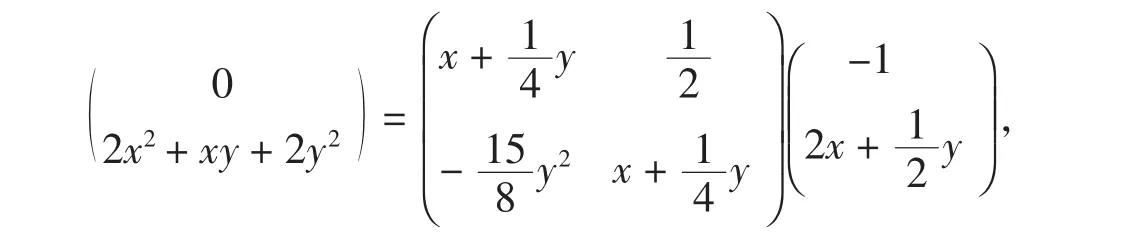
后面的步驟與文獻［6］例2.1一樣.

3.2 在構造偏微分方程組通解中的應用

文獻［2］給出了一種用機械化的方法構造一類微分方程組的通解.首先對微分方程組Au＝0在不同序下求出其標準型，從每個標準型中取只含某個未知函數的適當的方程作為目標方程Dυ＝0（其中，u，υ為函數列向量再利用矩陣多項式的綜合除法求原方程組Au＝0去除目標方程Dυ＝0所得的商與余，這時，一般情況下余式R＝0，從而得到變換公式和通解.關于標準型的概念及標準型算法可參考文獻［2］.下面以文獻［2］中的一個例子來說明矩陣多項式綜合除法的應用.

例2求方程組

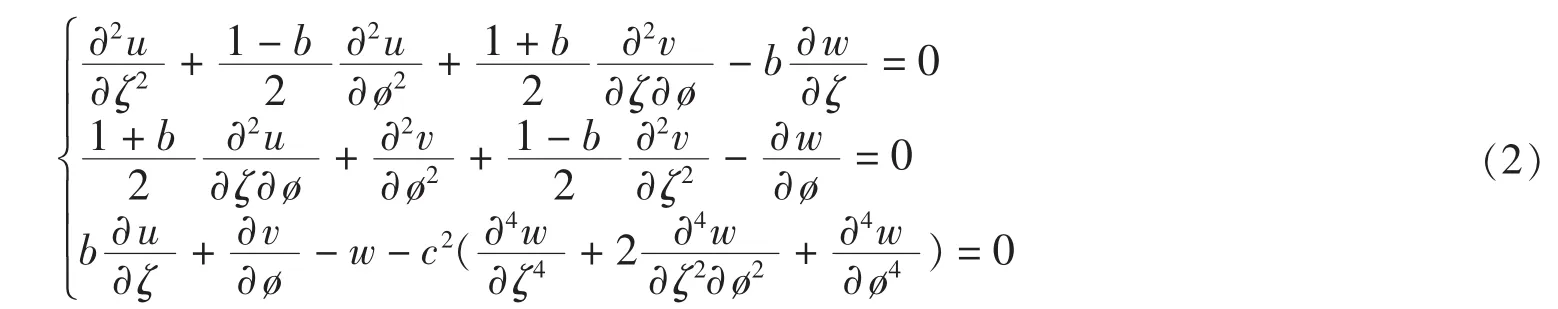
的通解（這里b、c是常數）.

解由文獻［2］可知目標方程可選為：

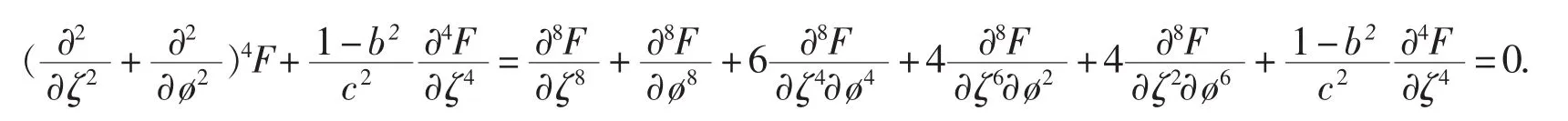
上述方程兩邊同時乘以c2，并改寫成多元多項式的形式為：

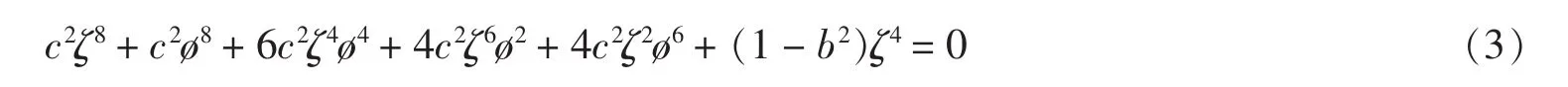
由于原方程組（2）有u、v、w3個未知函數，且關于這3個未知函數的“系數矩陣”為（偏微分算子均寫為多元多項式，并以變量ζ為主元，由于按總冪次展開時首項系數矩陣非行滿秩，故按行冪次展開）:

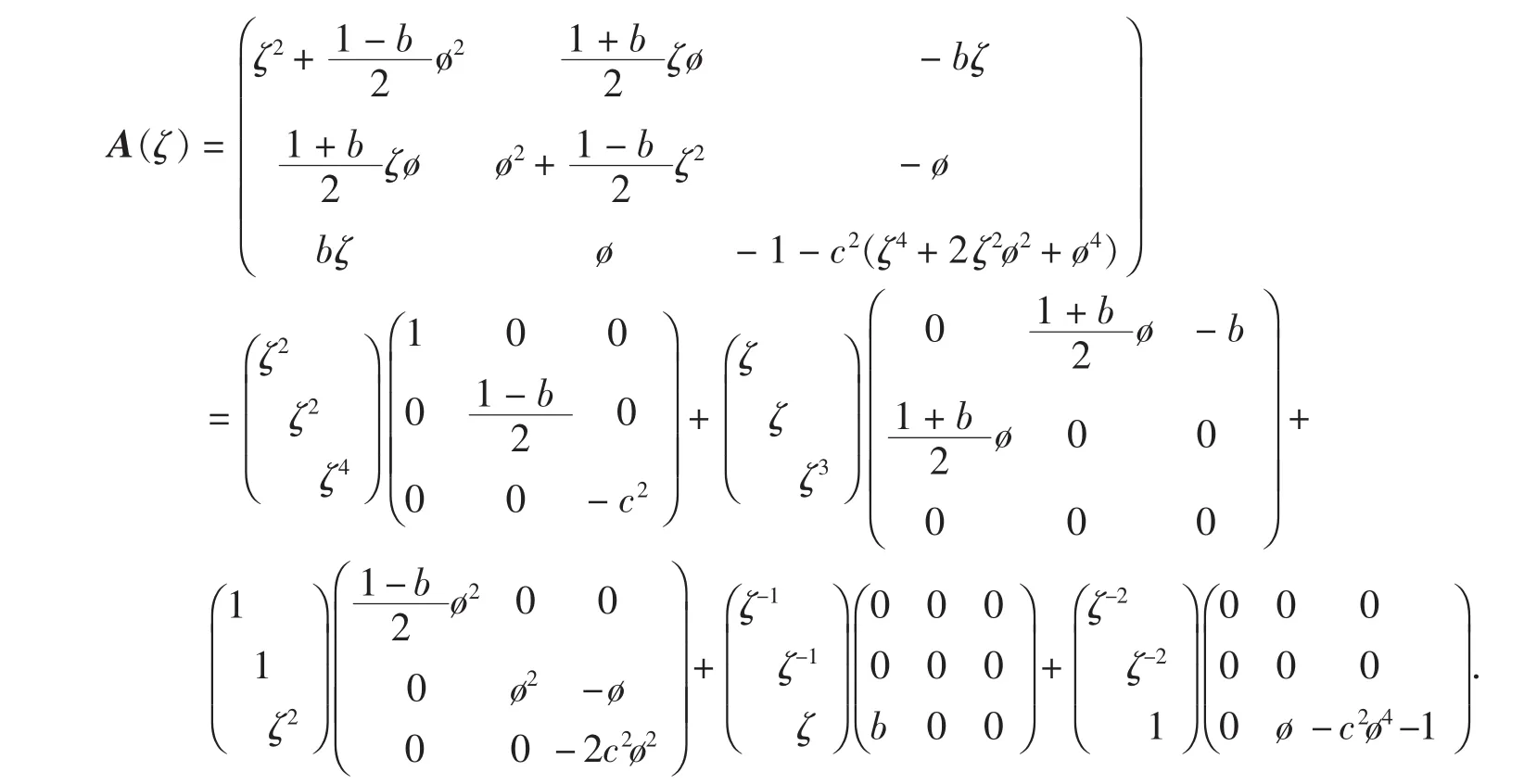
將主元為ζ的多元多項式（3）化為三階向量的形式，并按與“系數矩陣”相同的指定行冪次展開，得：

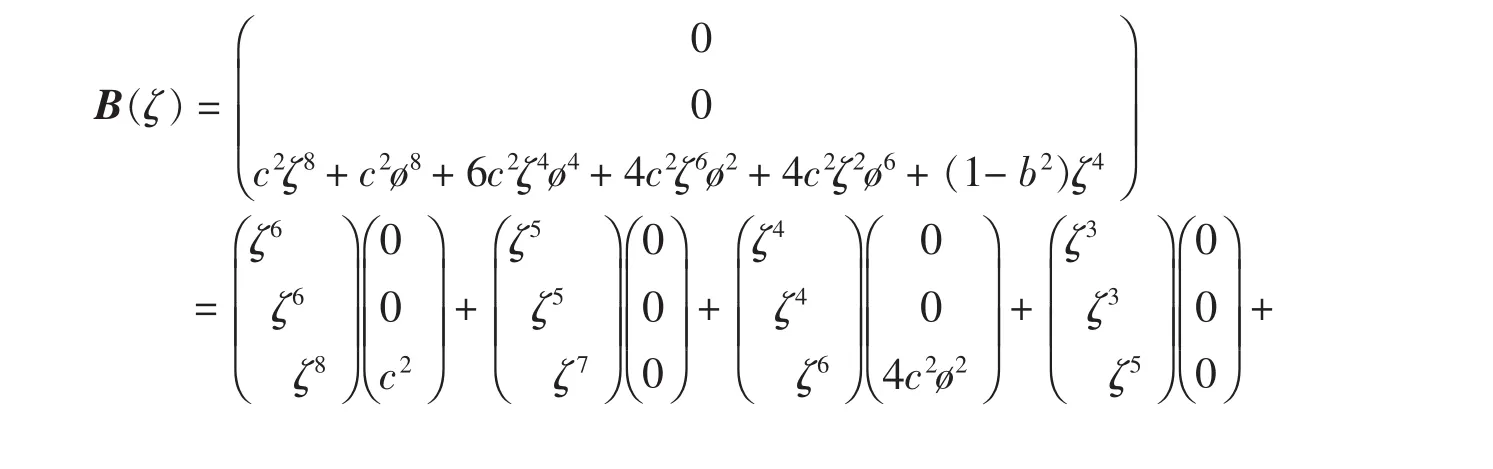
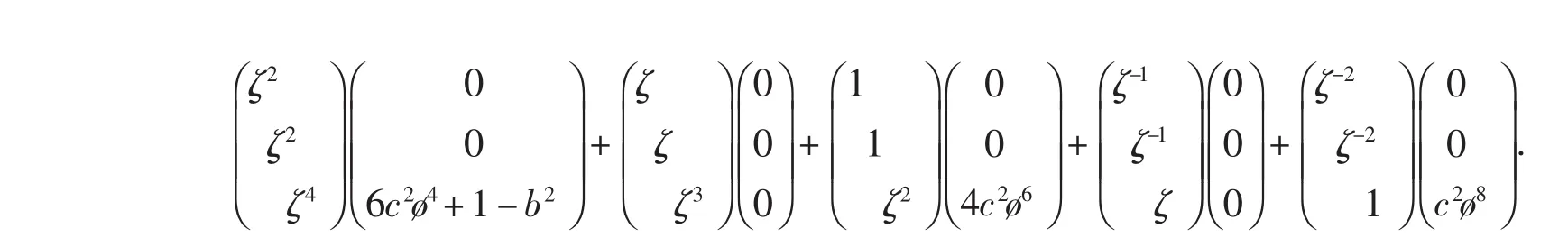
可知余式R（ζ）=O3×1（其中O3×1表示3×1的零矩陣），商式

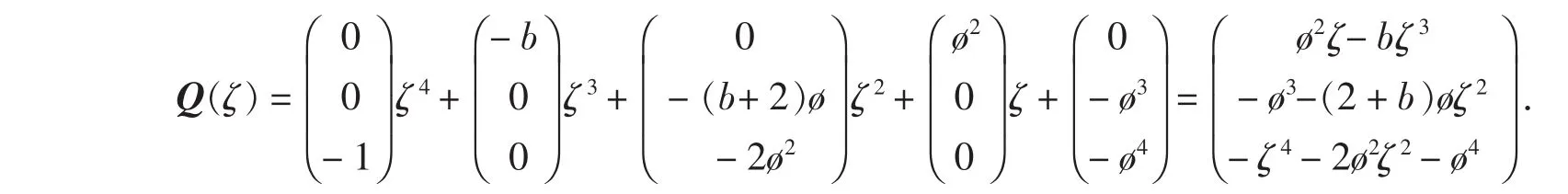
因此，有如下的分解式成立：

的通解[2].

本文類比多項式的綜合除法，給出矩陣多項式的綜合除法.該綜合除法除了解決矩陣多項式除法的求商式與余式問題，在實際應用中也有重要作用，如本文的例1和例2.不足之處就是礙于綜合除法的“形式”，需要人工計算，比較繁復.但從原理來看，該算法具有一般性，機械性，從而也可以在計算機上實現，而且有更好的計算能力.矩陣多項式的綜合除法可進一步推廣，如文獻[7]給出的升冪與降冪綜合除法.有關矩陣多項式綜合除法的更多推廣和應用仍有待于進一步的研究.

致謝：對汪立民教授的幫助謹致感謝.

[1] 阿拉坦倉，張鴻慶，鐘萬勰.矩陣多元多項式的帶余除法及其應用[J].應用數學和力學，2000，21（7）：661-667.

[2] 陸斌，張鴻慶.構造一類偏微分方程組通解的機械化方法及力學方程的自動推理[J].山東科技大學學報（自然科學版），2002，21（1）：18-24.

[3] 侯國林，阿拉坦倉.二元矩陣多項式的首一分解[J].內蒙古大學學報（自然科學版），2004，35（5）：490-494.

[4] 韓京清，許可康.線性控制系統理論——構造性方法[M].北京：科學出版社，2001：13-15.

[5] 羅宗虔.控制系統CAD常用算法基礎[M].武漢：華中理工大學出版社，1991：216-219.

[6] 阿拉坦倉.無窮維Hamilton系統的反問題[J].內蒙古大學學報（自然科學版），1998，29（5）：619-623.

[7] 謝澤嘉.升冪與降冪綜合除法在線性控制系統中的應用[J].韶關學院學報，2009，30（9）：8-13.

Synthetic Division of Matrix Polynomial and Its Application

XIE Ze-jia
（School of Mathematical Sciences,South China Normal University,Guangzhou 510631,Guangdong,China）

The synthetic division of matrix polynomial is given and will，on the basis of differential algebra,be applied in the problem solutions pertaining to the transformation fromconstantcoefficientpartialdifferentialequotiontotheinfinitedimensional Hamiltonian system.In addition，combined with thestandard formalgorithm，the synthetic division of matrix polynomial also finds application in constructing general solutions for a class of partial differential equations.

infinite dimensional Hamiltonian system；division with remainder；synthetic division；matrix polynomial；general solutions of partial differential equations

O 175.25

A

1001-4217（2010）02-0016-08

2009-12-01

謝澤嘉（1987-），男，廣東揭陽人，本科.研究方向：數學與應用數學.E-mail：1051863526＠qq.com