一種基于二次譜線生成的碼速率識別方法*
(中國電子科技集團公司第三十研究所,成都 610041)
1 引 言
正交頻分復用(Orthogonal Frequency Division Multiplexing ,OFDM)是一種多載波調制技術,由于具有較強的抗多徑、抗碼間干擾性能和高頻譜利用率,近年來在高速數據通信中得到了廣泛應用。OFDM技術還易于和其它多種接入方法結合使用,構成各種OFDM系統,其中包括MC-CDMA系統、Hop-OFDM系統,以及OFDM-TDMA系統等。這些與OFDM相關的新技術都具有良好的發展前景[1-3]。與此同時,OFDM傳輸系統也給無線電監測等領域帶來一系列新的課題,比如怎樣實現OFDM系統信號的盲接收等。其實,OFDM系統信號的盲接收技術不僅適用于監測領域,還能用于自適應OFDM系統[4]。自適應OFDM系統利用調制方式的靈活性,可以隨著信道信息的變化而自適應地調整調制參數,如編碼方式、碼元速率等,是一種智能化的通信方式。在自適應OFDM系統中,為了提高系統的頻譜效率,在接收端也采用了盲接收方式[6-7]。碼速率是數字通信系統的重要參數。碼速率未知時,就無法完成OFDM系統解調器的設計;其次,如果碼速率識別不正確,將OFDM信號進行不正確的解調也會部分或者全部破壞信號攜帶的信息。所以,識別碼速率等參數是OFDM系統的盲接收過程中一個必不可少的步驟[8-10]。
通過文獻檢索尚未搜索到對OFDM系統有較好識別率的方法,為此,本文提出了一種識別精度高、實用性強的OFDM系統碼速率識別方法,核心思想是利用了信號的二次生成譜線特性。信號的二次生成譜線能夠提供特有的信號特征用以識別碼速率。這種方法在較低信噪比條件下可以實現對OFDM系統碼速率的有效識別。
2 基于二次譜線生成的OFDM系統碼速率估計
2.1 OFDM信號模型
OFDM系統中的信號是在頻域內將信道分成多個子信道,在每個子信道上使用獨立的子載波分別調制,并且進行并行傳輸的一種信號。
在OFDM系統中,信號第二次生成的譜線具有更豐富的參數特征。要利用該特性對信號進行碼速率識別,則需要首先分析信號的二次生成譜線結構。由于OFDM調制方式的靈活性,使得發射端可以有很多組合方式,例如各子載波的信號調制方式可以是BPSK、QPSK、16QAM與64QAM等。
為描述方便而又不失一般性,OFDM系統傳輸的信號可表示為

(1)
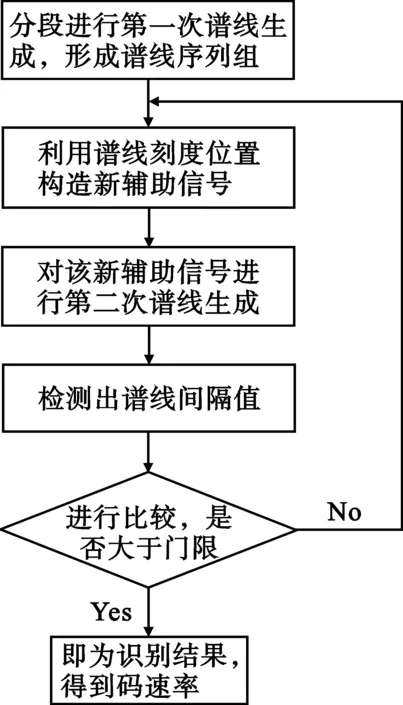
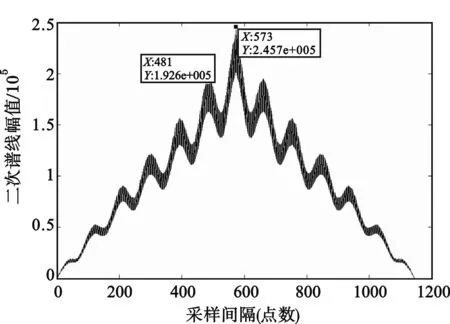
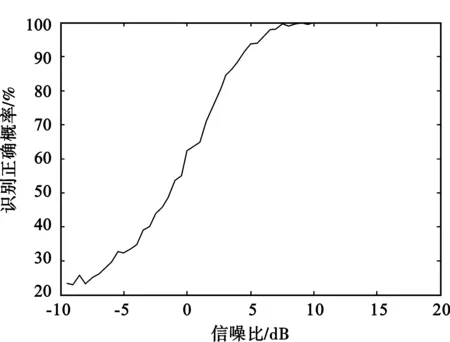
式中,f0是載頻;φ0是初始相位;ck,n來自有限符號的星座;q(t)為成形脈沖;T0為脈沖寬度;t0為脈沖的起始時間,|t0| x(t)還可以表示為 x(t)=Re{r(t)ej(2πf0t+φ0)} (2) 其中: (3) 可以得出: (4) gk(t)即為子載波上的傳輸波形,因為Δf=1/T0,所以ej2πkΔf(-nT0)=1,故: (5) (6) 式中,q(t)為成形脈沖,Q(f)是q(t)的傅里葉變換,f為第一次生成譜線刻度,F為第二次生成譜線刻度。 OFDM系統的信號二次生成譜線經推導可表示為 (7) 該方法包括以下幾個基本步驟: (1) 利用OFDM系統的信號分段進行第一次譜線生成,形成譜線序列組; (2) 對該譜線序列組,利用譜線刻度位置形成新輔助信號; (3) 對該新輔助信號序列進行第二次譜線生成,形成第二次譜線序列; (4) 對第二次譜線序列檢測出譜線間隔值,并將該值與設定的門限值進行比較,如果大于門限,即為OFDM系統碼速率,算法終止;當小于門限時,則回到步驟2。 基于二次譜線生成的OFDM系統碼速率識別流程如圖1所示。 圖1 基于二次譜線生成的碼速率識別流程圖 下面以一示例說明基于二次譜線生成的OFDM系統碼速率識別流程。假設OFDM的信號序列長度為l=m×n,即為{x(1),x(2),x(3),…,x(mn)},先對其分段,每段為m點長度序列,一共n段,如圖2所示。 圖2 OFDM的信號序列分段示意圖 然后,分別對每段序列進行傅里葉變換,得到第一次譜線生成序列,長度為l=m×n,如圖3所示。 圖3 輔助序列構造示意圖 在此基礎上,從第一次譜線生成序列中的每段數據中同一頻點(頻點任選)上的譜線生成值,選取它們出來構造輔助序列,比如可選每段數據第二個頻點譜線值構造輔助序列,即{X(2),X(m+2),X(2m+2),…,X((n-1)m+2)},用虛線框標注如圖3所示。再次對新輔助序列進行傅里葉變換,得到長度為n的二次譜線序列可表示為:Y(1),Y(2),Y(3),…,Y(n),從而得到二次譜線間隔。 最后,把得到的二次譜線間隔與根據大量的仿真試驗得到的門限相比較,如果大于門限,即可得到識別的碼速率結果;如果小于門限,重新選擇第一次譜線數據,并構造新的序列,繼續進行二次譜線和門限判決,如此循環,直至第一次譜線數據循環完結。 通過仿真對基于二次譜線生成的OFDM系統碼速率識別方法的正確性進行驗證。以下為仿真參數:在OFDM系統中,信號各路子載波采用QPSK調制,一共16個子載波,同步載頻1個子載波,數據調制載頻15個子載波,每幀信息的采樣點為93點,采樣率為7 040 Hz,采樣率和碼速率比值為3.128,加性高斯白噪聲環境。在信噪比為5 dB時,對該OFDM系統的二次生成譜線進行分析,結果如圖4所示。 圖4 信噪比為5 dB條件下的二次譜線分析圖 通過圖4可看出二次譜線出現明顯的周期性變化,計算峰值間隔為93個采樣點與OFDM系統參數相符合,從而可以推算出該OFDM系統的碼速率。 為了驗證該方法的有效性和性能,對-10~20 dB范圍的信噪比進行了大量仿真。圖5給出了在不同的信噪比條件下加性高斯白噪聲信道中,1 000次Monte Carlo的OFDM碼速率正確識別概率曲線。 圖5 基于二次譜線生成的碼速率識別方法正確率曲線 從仿真結果可見,在信噪比大于3 dB時,識別正確率在90%以上。因此,該方法能夠在較低信噪比下識別OFDM系統信號的碼速率。該仿真結果也驗證了本文提出的碼速率識別方法的有效性。 本文提出了一種基于二次譜線生成的碼速率估計方法,通過在各種信噪比下的多次仿真試驗證明該方法能夠有效地識別OFDM系統的碼速率,有效地解決了OFDM系統碼速率識別問題。不僅識別概率高,而且具有較強的抗噪性,能識別各子道相異調制模式,對OFDM系統的盲接收和自適應OFDM系統的研制等具有很強的實用價值。 同時,本方法稍加改進后也可以對其它多種信號的碼速率進行有效估計,能夠應用于多種通信系統,這將是筆者今后進一步研究的方向。 參考文獻: [1] 王文博,鄭佩.寬帶無線通信OFDM技術[M]. 北京:人民郵電出版社,2003. WANG Wen-bo, ZHENG Pei. The Technology of OFDM wide-band wireless communication[M].Beijing:People′s Posts and Telecom Press, 2003.(in Chinese) [2] 張賢達,保錚. 通信信號處理[M].北京:國防工業出版社,2000. ZHANG Xian-da, BAO Zheng. Communication signal processing[M].Beijing: National Defense Industry Press,2003. (in Chinese) [3] Michael Speth, Stefan A Fechtel, Gunnar Fock,et al. Optimum receiver design for Wireless broad-band systems using OFDM[J]. IEEE Transactions on Communications,1999, 47(11):1668-1677. [4] Swami A,Sadler B M. Hierarchical Digital Modulation Classification Using Cumulants [J]. IEEE Transactions on Communication,2000,48(3):416-429. [5] Keller T,Hanzo L. Adaptive modulation techniques for duplex OFDM transmission[J]. IEEE Transactions on Vehicular Technology,2000,49(5):1893-1906. [6] Umebayashi K,Ishii S,Kohno R. Blind adaptive estimation of modulation scheme for software defined radio[C]//Proceedings of IEEE International Symposium on Personal,Indoor,Mobile Radio Communication.London:IEEE,2000:43-47. [7] Lottici V,Luise M,Marselli M,et al. Blind Subcarrier Frequency Ambiguity Resoluntion for OFDM Signals over Selective Channels [J]. IEEE Transactions on Communication,2004,52(9):1532-1537. [8] Liu C,Li F. Spectrum modeling of OFDM signals for WLAN[J]. IEE Electronics Letters,2004,40(22):1431-1432. [9] Richard van Nee Ramjee Prasad. OFDM for Wireless Multimedia Communications[M]. Boston,London:Artech House,2000:80-88. [10] Luise M, Marselli M, Reggiannini R. Low-complexity Blind Carrier Frequency Recovery for OFDM Signals Over Frequency-selective Radio Channels[J]. IEEE Transactions on Communication, 2002,50(7): 1182-1188.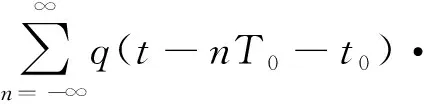
2.2 OFDM信號的二次生成譜線分析
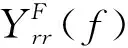
2.3 方法步驟和流程
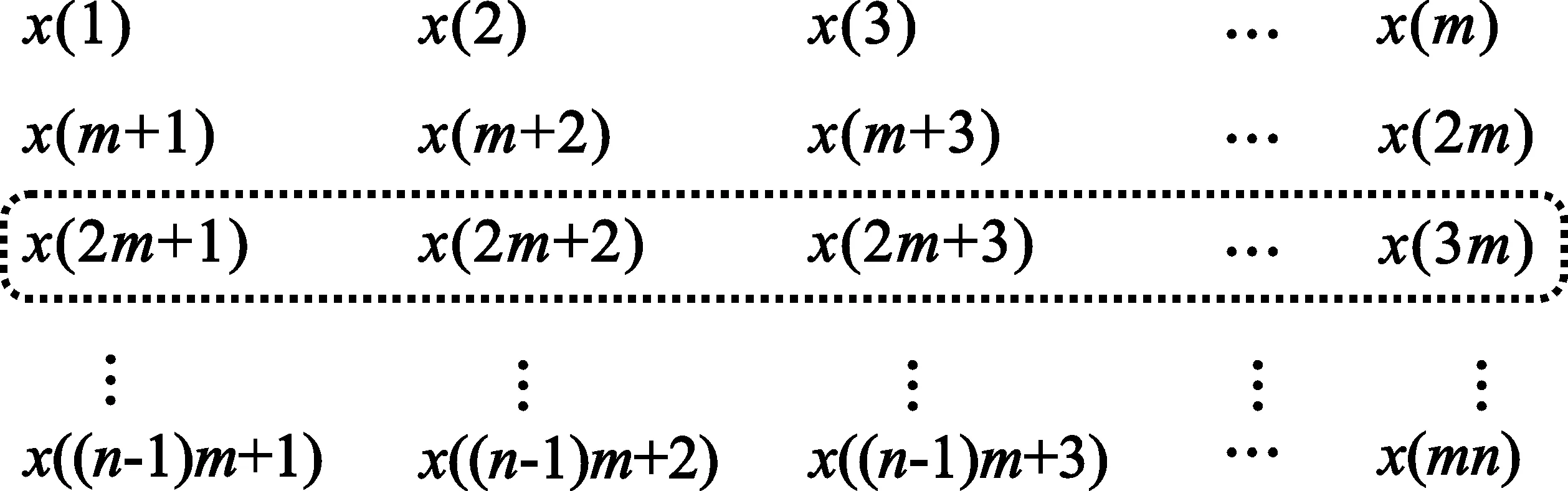
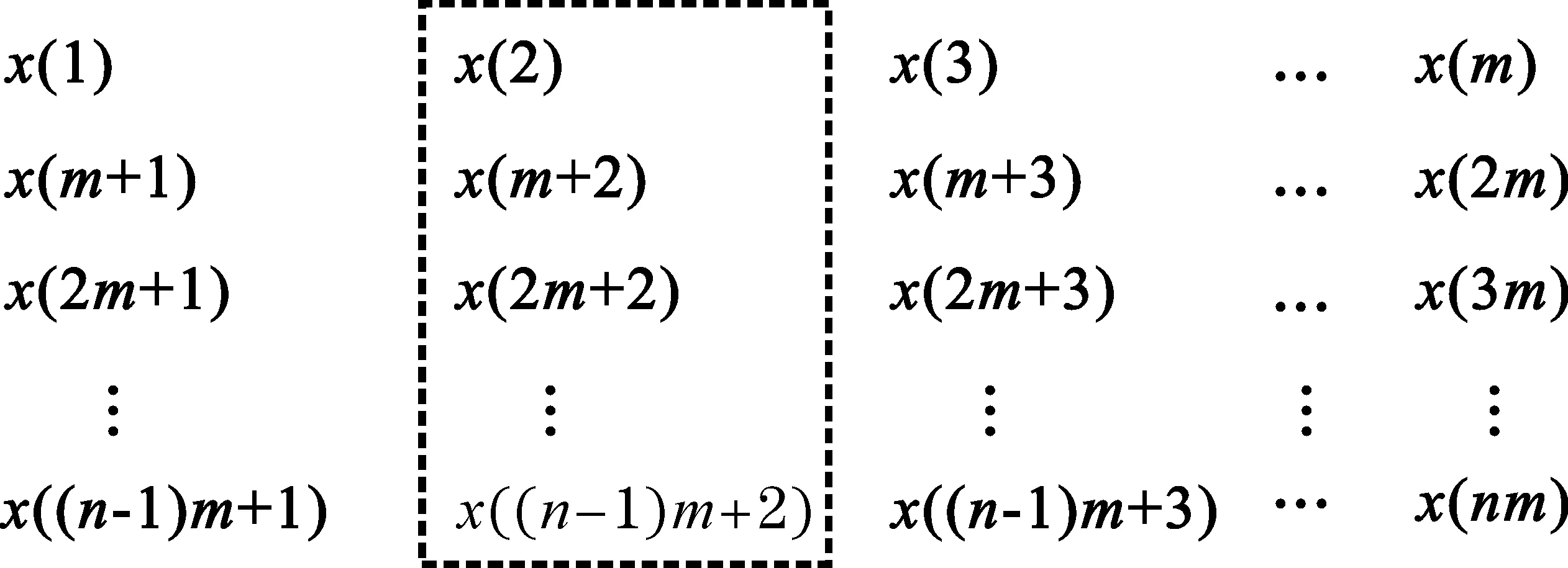
3 仿真驗證
4 結束語

