基于短時傅里葉變換的相位編碼信號分析*

(中國西南電子技術研究所，成都 610036)

1 引 言

在現代戰爭中，輻射源的識別對許多重大戰略決策具有重要的指導意義。隨著新體制雷達的不斷出現和雷達信號形式的日益復雜，傳統的分析方法己經不能滿足電子偵察的要求。電子對抗除了要求對雷達信號進行常規的分析，如到達時間、到達角、載頻、脈沖寬度、脈沖重復頻率和極化方式等之外，還必須對雷達信號脈內細微特征進行分析和提取，以便有效地識別雷達信號，判斷目標的威脅程度。因此，詳細分析雷達信號的各種細微特征，包括脈內、脈間和脈組的細微特征及有意和無意的調制，將為雷達信號的分選和識別提供有力的幫助。

雷達信號脈內調制特性分析起源于21世紀80年代初，國內外已經作了大量的研究，有多種估計算法和相關技術,主要包括譜相關分析法、調制域分析法、數字中頻處理法[1-2]等。在有些應用場合，如要求準確識別相同相位編碼調制樣式的信號時，僅僅知道其調制樣式是不夠的，還必須對編碼序列進行恢復，從而準確判斷出具有相同調制樣式但具有不同編碼序列的信號。因此，上述方法還存在一定缺陷。

由于相位編碼信號在相位跳變處有突變特性，本文提出的利用短時傅里葉變換(STFT)得到信號的時頻分布，通過相參積累的方法找到相位編碼信號的跳變位置，從而檢測碼元；最后，通過分析跳變位置處相位的變化情況，恢復得到編碼信息。該方法的優勢在于在較低信噪比情況下也可以得到較好的解碼結果，在工程上有一定的應用價值。

2 算法原理

2.1 短時傅里葉變換

對于時間信號f(t)，其窗口Fourier變換定義為

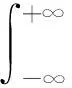
(1)

當窗口函數滿足一定的標準化條件時，具有反演公式：

(2)

滿足窗口函數條件為：t·g(t)∈L2(R)和g(t)∈L2(R)的窗口Fourier變換稱為短時傅里葉變換，二維函數F(ω,τ)(-∞<ω<∞,-∞<τ<∞)反映了信號f(t)在時刻τ附近的局部頻譜特征，隨著τ的推移，F(ω,τ)刻畫了信號f(t)在時、頻兩域的信息。

STFT是通過窗函數g(t)將一維信號f(t)映射成時間-頻率域上的二維函數。它的主要優點是若信號f(t)在給定的時間間隔和頻率間隔內具有大多數能量，則其STFT將局域化于該區域內；而在信號沒有多少能量的時間和頻率間隔處，其STFT接近為0；其主要的缺陷在于對所有頻率都使用單一的窗函數，所以STFT的分辨率在時間-頻率域內處處相同。

2.2 滑動窗的短時傅里葉變換遞歸算法

在實際應用中，需要對式(1)進行離散化，同時為了得到信號的時頻特性，還要對信號進行滑動取值。設x(m)與g(m)(m=0,1,2,…)分別為離散時間信號與窗函數，設選取窗口長度為L，則有：

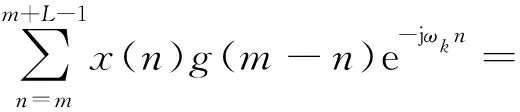
令

則：

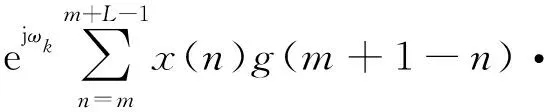
e-jωk(n-m)-x(m)g(1)ejωk+

x(m+L)g(L-1)e-jωk(L-1)=

[T(m,k)-x(m)g(1)]ejωk+

x(m+L)g(L-1)e-jωk(L-1)

(3)

式中，代表時間標尺的m在樣點范圍[0，N-1]內滑動取值；L為計算STFT的時間窗長度；頻率點ωk在信號頻率范圍[2π(f0-B/2),2π(f0+B/2)]內等間隔取樣。因此利用遞歸算法，滑窗STFT與小波變換等方法比較，可以大大提高運算速度。

2.3 相位編碼信號碼元檢測

要獲得相位編碼信號的碼元檢測曲線，需要利用短時傅氏變換的結果求出相鄰數據段之間的相參性。為此，定義如下時間序列作為信號的瞬時相參度指標：

η(m)=|T(m,ωa)|+|T(m+L,ωb)|-

|T(m,ωc)+T(m+L,ωc)e-jωcL|

(4)

式中，ωa、ωb分別為|T(m,ωk)|和|T(m+L,ωk)|的峰值頻率，而ωc的取值為

(5)

從以上定義可見，η(m)在信號相位出現不連貫突變時刻呈現出峰值。因此，通過對η(m)序列進行峰值檢測，即可以檢測出碼元及其邊緣位置(時刻)。門限可以根據η(m)中的最大值ηmax由經驗來確定。

2.4 相位的估計

要恢復相位編碼信號的編碼序列，需要獲得跳變點處的相位信息。為適應較低的信噪比要求，可將長脈沖數據按樣點數L均勻分割成M段，對每段進行相關積累以提高信噪比。假設已經粗測得信號的頻率為fc，對各段信號進行相關積累如下：

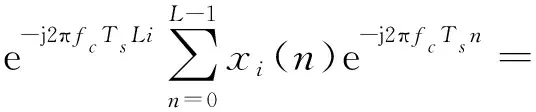
L·Aej(φi-2πfcTsLi+θ)+ni

(6)

式中，θ=π(fo-fc)(L-1)為常量，ni為混在信號中的噪聲分量的譜相關結果。對于常規信號，由于第i段數據的初相φi=φo+2πfoTsiL，因此，yi可表示為

yi=L·Aej(φo+θ+2π(fo-fc)TsiL)+ni=

L·Aej(β0+2πfΔTsiL)+ni

(7)

式中，相位常量β0=φo+θ，頻率殘差fΔ=fo-fc。測量yi的相位并解相位模糊得：

βi=β0+2πfΔTsiL,i=0,1,2，…,M-1

(8)

利用最小均方誤差準則由式(8)可以估計頻率殘差分量和初相，其估計式為

(9)

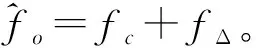
2.5 相位編碼信號分析

對PSK信號的分析主要利用測量到的碼元初相參數，同時也必須利用頻率測量結果來進行時間上的同步。總結以上分析可得解碼步驟如下：

(1) 求出頻率序列的平均頻率作為信號的中心頻率；然后從第一個碼元初相測量值開始，根據中心頻率預測下一碼元的初相，與該碼元的實測值相減，得到相鄰碼元的相位差序列；

(2) 令第一個碼元的符號為零，下一個碼元符號則根據它與前面碼元的相位差來確定，若相位差是π/2的k倍(四舍五入)，則其符號為上一碼元符號加上k；

(3) 依此往下推，解算出所有碼元；

(4) 對所有碼元按4取模運算，將符號值調整在0～3之間；

(5) 檢測編碼符號中是否有1或3，如果無則信號被識別為二相編碼信號，并將所有符號除以2，得到二相編碼信號的解碼；如果有，則信號被識別為四相編碼信號，其解碼結果不變。

3 仿真實驗

3.1 相位編碼信號分析結果

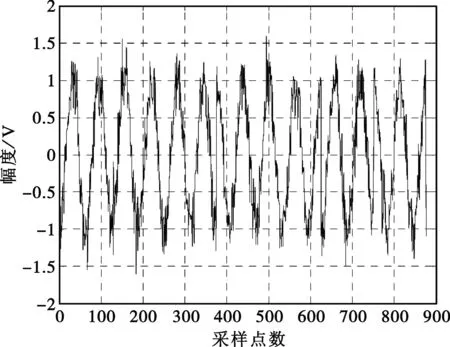
圖1 10 dB BPSK信號

圖2 短時傅里葉變換結果

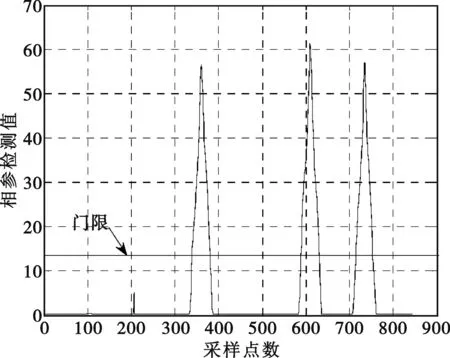
圖3 檢測碼元跳變點曲線

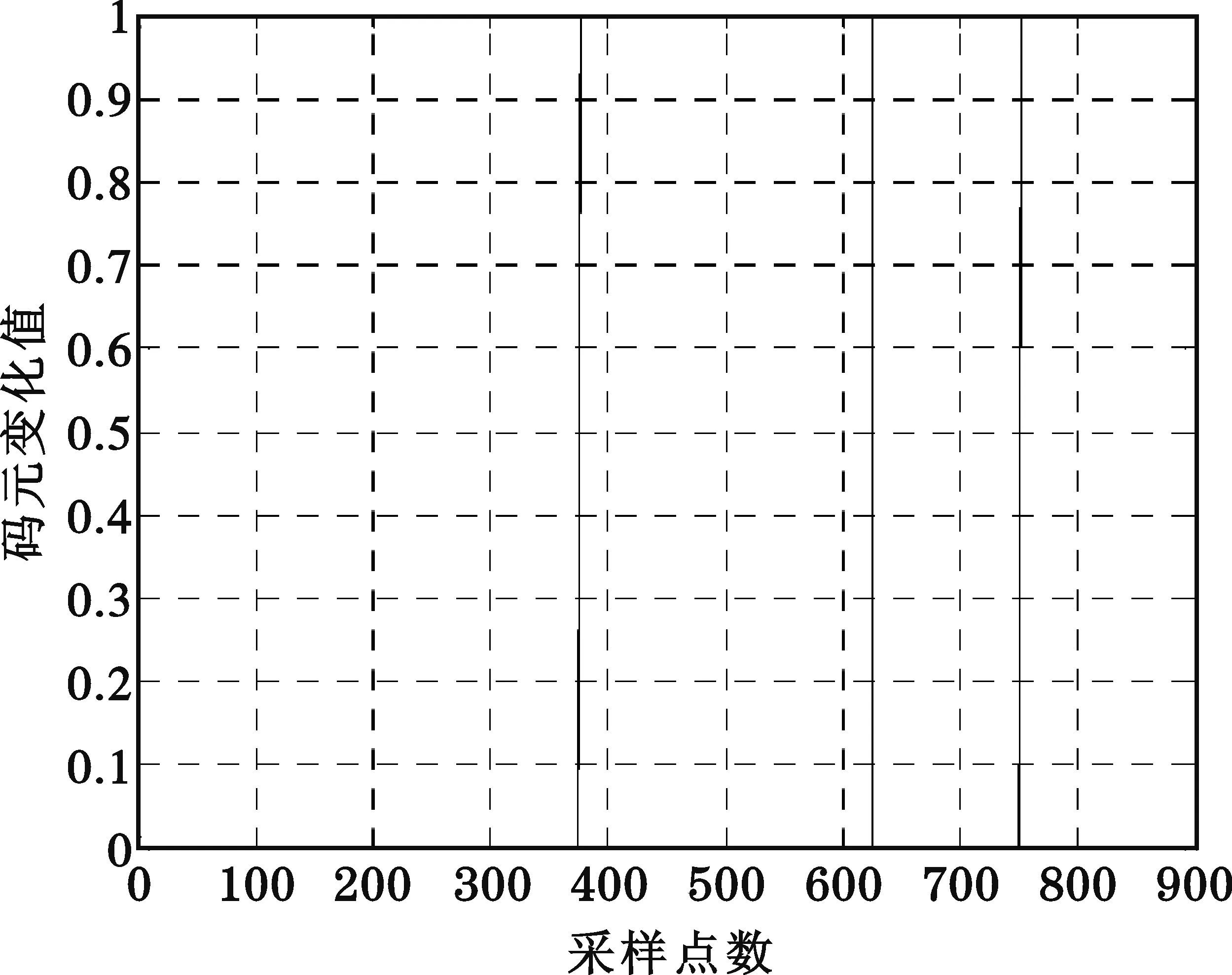
圖4 解碼結果

為了驗證方法的有效性，我們分別對BPSK和QPSK信號進行了仿真分析。圖1～4是BPSK信號的分析結果，其中BPSK信號選用了7位Barker碼，信號載頻4 MHz，碼寬0.5 μs，采樣頻率為250 MHz，信噪比為10 dB。

圖5～8是QPSK信號的分析結果。其中QPSK信號選用了16位Frank碼，信號載頻4 MHz，碼寬0.5 μs，采樣頻率250 MHz，信噪比10 dB。

由圖1～8可以看出，該方法能夠在較低信噪比情況下實現對相位編碼信號的頻率測量和解碼。

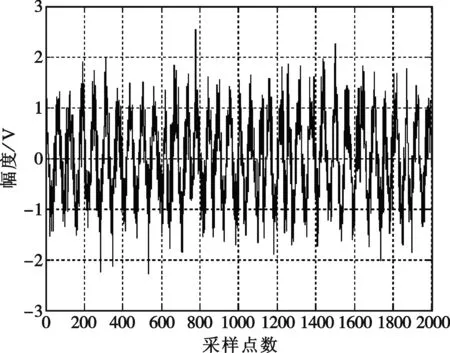
圖5 10 dB QPSK信號

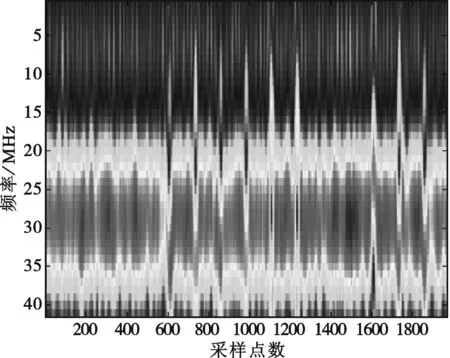
圖6 短時傅里葉變換結果

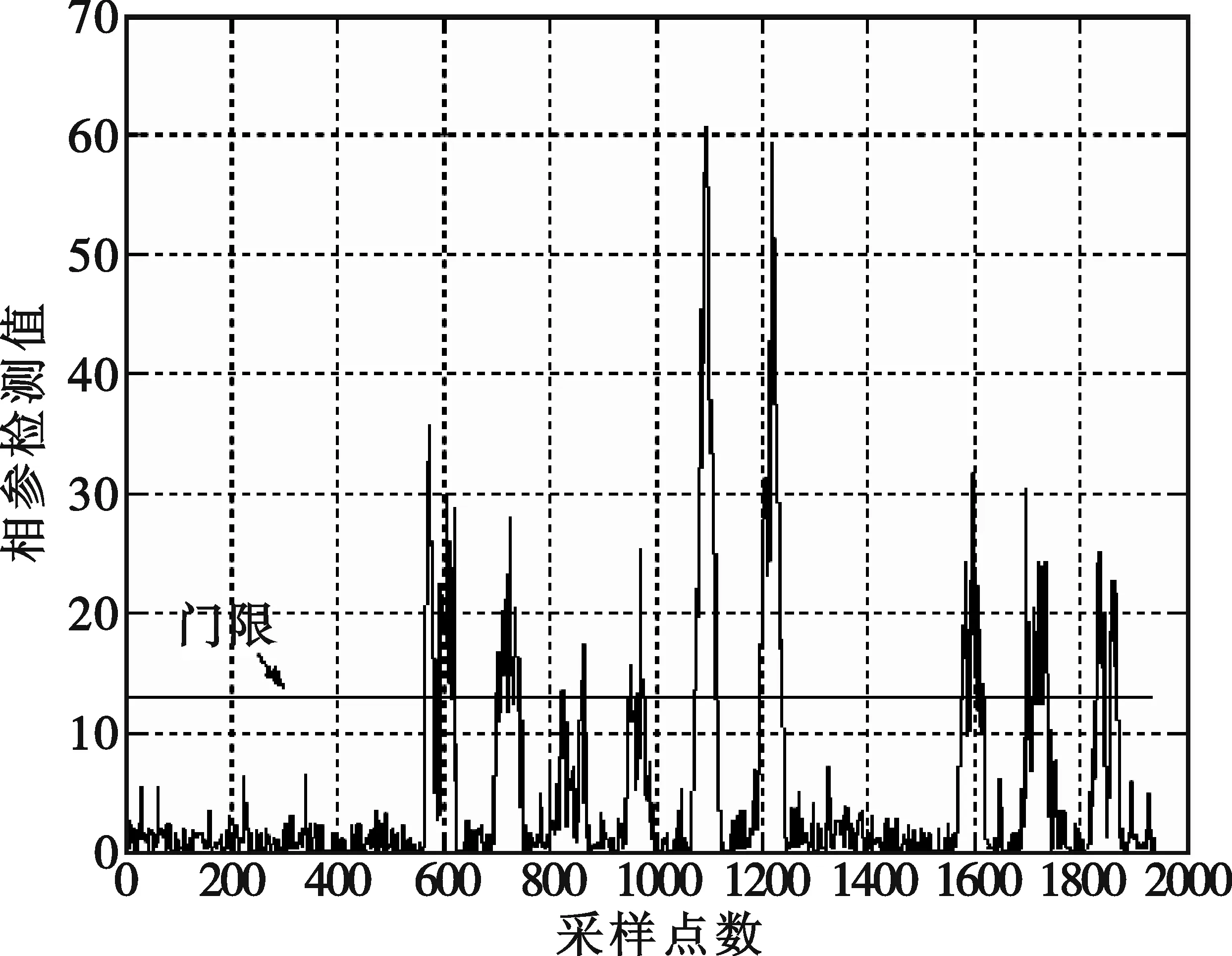
圖7 檢測曲線

3.2 窗函數選擇對算法的影響

為了分析短時傅里葉變換中窗函數對算法的影響，我們在不同信噪比和不同窗函數條件下分別對BPSK和QPSK信號進行了蒙特卡羅試驗。我們選取較有代表性的窗函數，包括矩形窗、漢明窗、Blackman窗、切比雪夫窗和Kaiser窗，最后統計得到解碼正確率，如圖9和圖10所示。

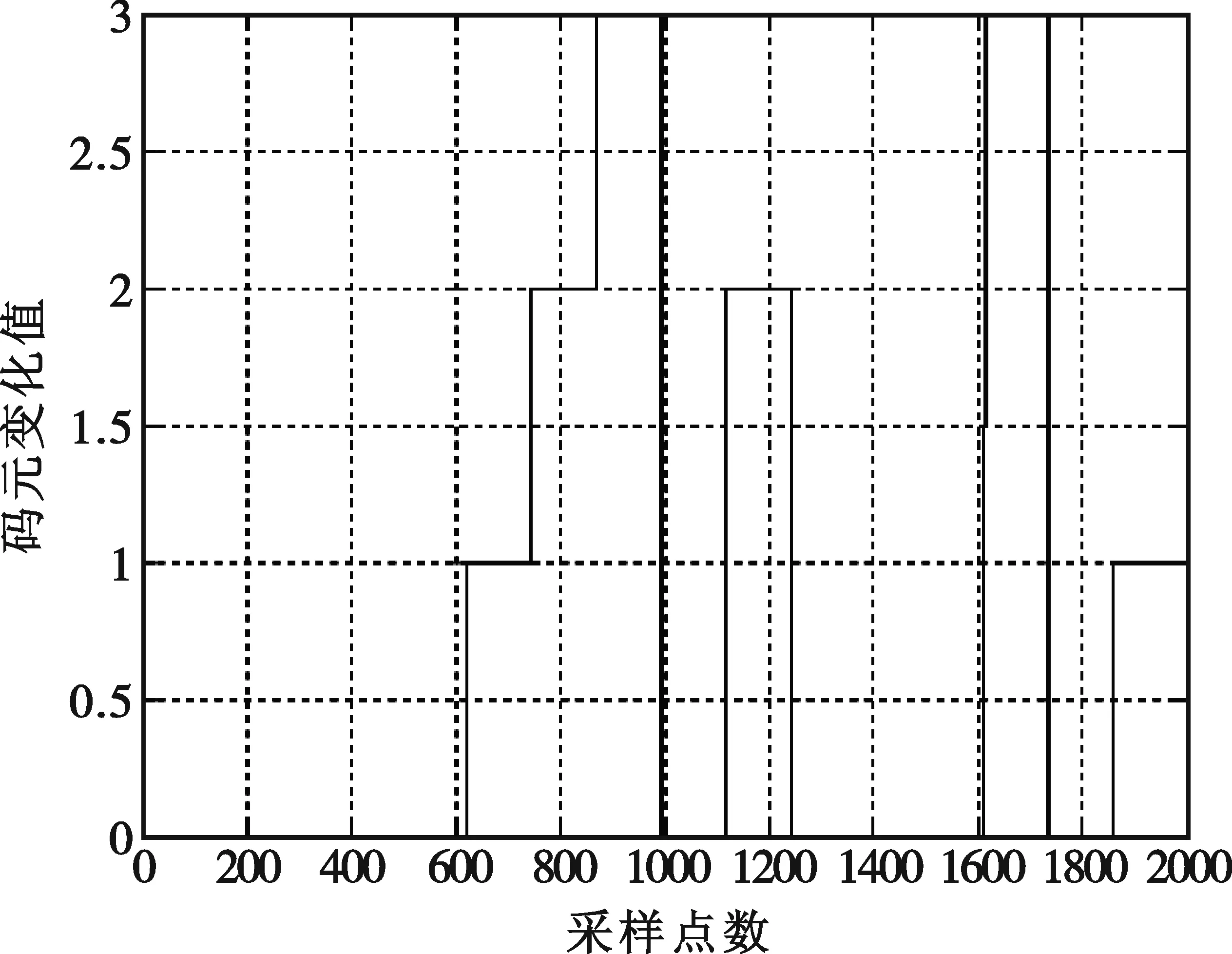
圖8 解碼結果

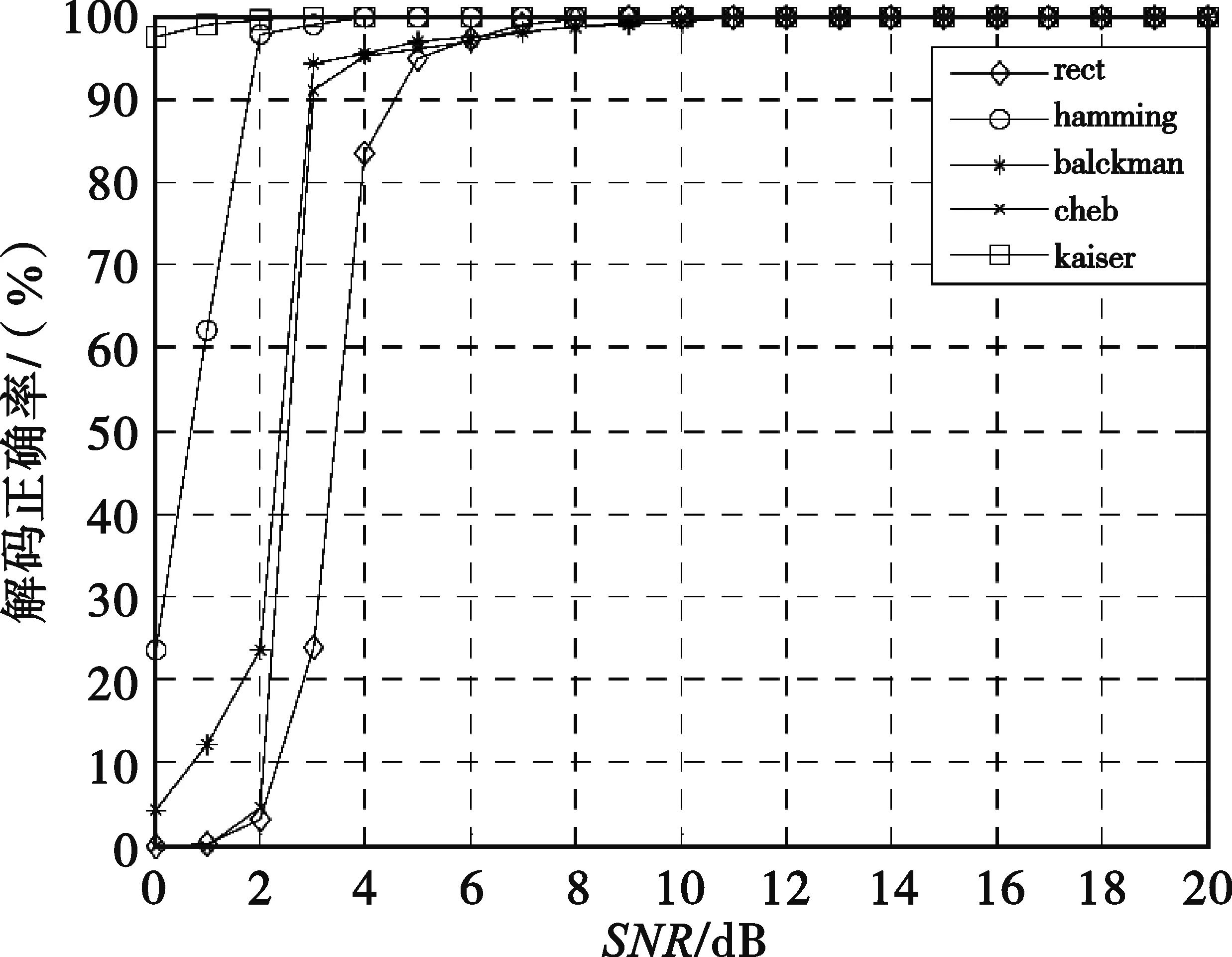
圖9 BPSK信號解碼正確率與窗函數的關系

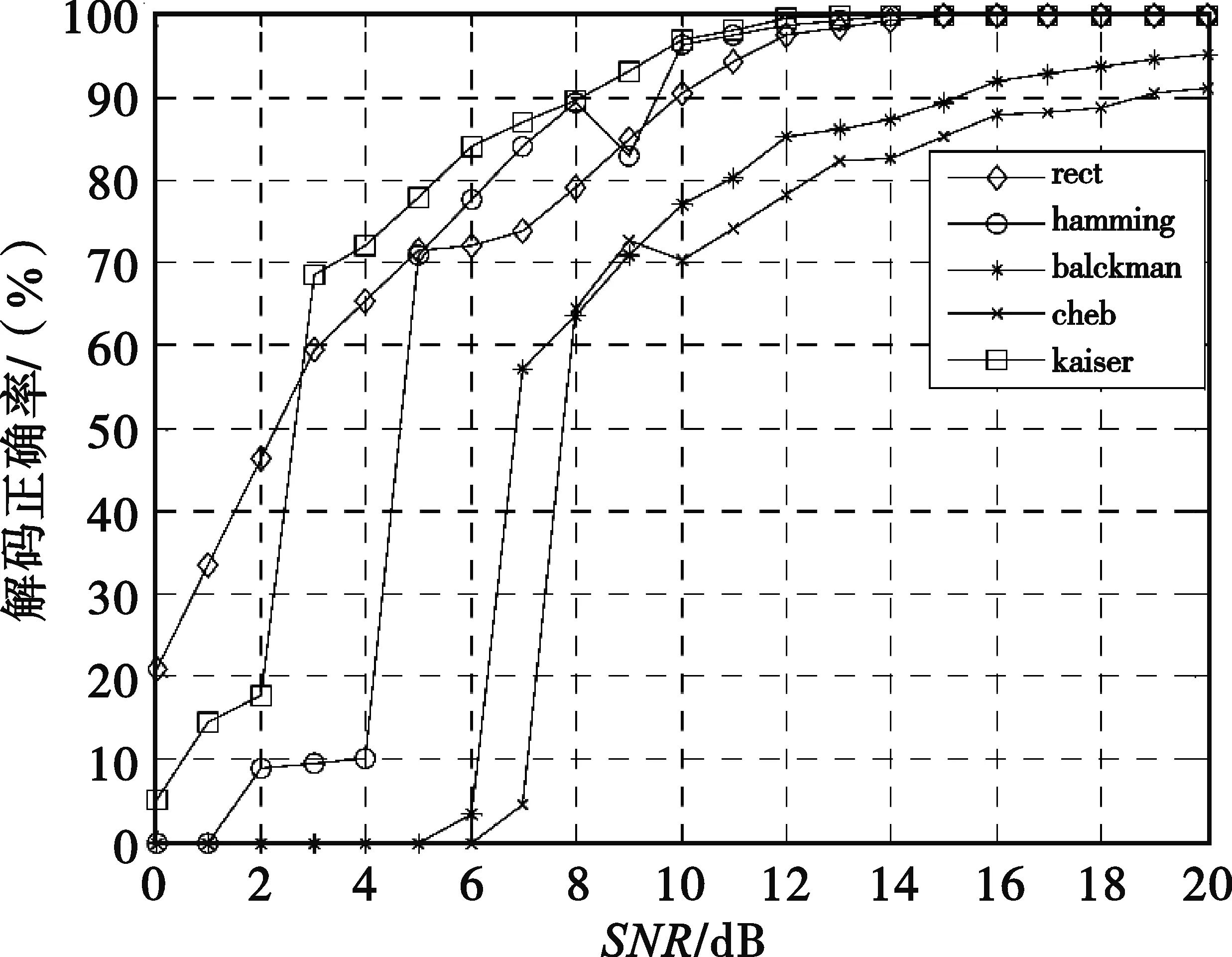
圖10 QPSK信號解碼正確率與窗函數的關系

由圖可見，窗函數的選擇對算法有一定影響，通過選擇合理的窗函數如漢明窗，能夠進一步降低算法對信噪比的要求。

4 結 論

本文根據相位編碼信號在相位跳變處的突變特性，采用短時傅里葉變換(STFT)結合相參積累的算法找到相位編碼信號的跳變位置，從而檢測到碼元；然后通過分析相位在跳變位置處相位的變化情況，恢復得到編碼信息。該方法與時頻分布、小波變換等方法比較，處理速度較快，在較低的信噪比情況下也可以得到較好的處理結果，在雷達信號細微特征分析等方面有一定的工程應用價值。

參考文獻：

[1] 黃知濤,周一宇. 一種有效的BPSK/QPSK信號調制識別方法[J]. 電子對抗技術, 2005, 20(2): 10-13.

HUANG Zhi-tao,ZHOU Yi-yu.An Effective Approach to the Recognition of BPSK/QPSK Signals[J].Electronic Warfare Technology,2005,20(2):10-13.(in Chinese)

[2] 趙冰,羅豐,吳順君. 相位編碼信號的譜相關分析與調制參數估計[J]. 雷達與對抗,2005(3):34-37.

ZHAO Bing,LUO Feng,WU Shun-jun.Spectral Correlation analysis and moducation Parameor Estimation of PSK Signals[J].Radar&Ecm,2005(3):34-37.(in Chinese)

[3] 穆世強，熊健，陳天麒. 脈內調制特性的中頻解調分析[J].電子科技大學學報,1993, 22(3):237-242.

MU Shi-qiang,XIONG Jian,CHEN Tian-lin. Analysis of IF Demodulation with intra-pulse Modulation Characteristics[J].Joural of University of Electronic Technology of China,1993,22(3):237-242.(in Chinese)