采用偏心率和傾角矢量聯合隔離法實現雙星共位*

(解放軍61081部隊，北京100094)

1 引 言

隨著航天技術的不斷發展，氣象衛星、導航衛星、通信衛星等在各自領域發揮了日益重要的作用。全球每年發射的衛星數量在不斷增多，其中地球同步軌道衛星占有比例最高。根據國際電聯相關規定，地球同步衛星的位置保持精度約為±0.1°，并且衛星之間需要保持一定的安全距離，因此地球同步軌道資源極為有限。然而，某些衛星由于工作頻段需要，必須工作在特定的地球同步軌道位置區域，如果該特定區域已有衛星正在運行，新發射衛星就需要和已有衛星長期共位運行，在滿足每顆衛星位置保持精度的前提下不能發生相互碰撞和相互遮擋。在國際上，多星共位技術比較成熟，雙星共位較為普遍，最多達到五星共位。國內衛星共位技術正在不斷成熟，但理論方法應用于工程實踐還有許多問題需要解決。目前，工程實施上比較可行的方法有絕對偏心率隔離法、相對偏心率隔離法、偏心率矢量和傾角矢量聯合隔離法以及經度隔離法等[1-2]。本文對偏心率矢量和傾角矢量聯合隔離法進行雙星定位的工程實踐進行了論述，通過雙星定位的成功實踐能夠驗證該方法及控制策略的合理性和有效性。

2 偏心率矢量和傾角矢量聯合隔離法

用于描述衛星軌道位置的主要參數[1-3]有：

平經度漂移率：D=-1.5(a-as)/as；

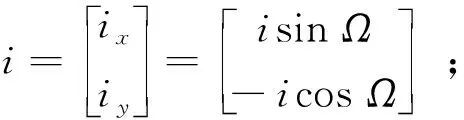
平赤經：L=Ω+ω+M；

式中，a為衛星半長軸，as為理想地球同步軌道半長軸，Ω為升交點赤經，ω為近地點幅角，M為平近點角。

為了避免兩個衛星相互碰撞和相互遮擋，需要調整和控制兩顆衛星之間的距離，使之始終大于安全距離，從而保證兩顆衛星各自運行在安全可控的軌道范圍之內。調整兩星距離的手段主要是利用合理的衛星隔離方法制定工程上可行的衛星軌道控制策略，并分階段實施，從而達到衛星軌控效果。衛星隔離的原理是將衛星之間距離分解為3個方向的距離分量，即徑向距離分量、切向距離分量和法向距離分量，只要保證其中一個或一個以上距離分量大于安全距離的最低要求，即可保證兩顆衛星的安全隔離。也可用偏心率矢量和傾角矢量來描述兩星之間的距離，兩顆衛星傾角矢量之差可用兩星之間法向距離表示；兩星偏心率矢量之差可用兩星在徑向和經度方向的距離表示。因此，衛星共位的前提是保持兩星偏心率矢量之差和傾角矢量之差大于安全距離。

偏心率矢量和傾角矢量聯合隔離法的基本思想是使兩顆衛星的偏心率矢量差和傾角矢量差滿足一定條件，即當兩顆衛星在地球垂直赤道面的法向距離相等時，確保兩顆衛星徑向距離不相同，從而實現兩星隔離。應用偏心率矢量和傾角矢量聯合隔離技術時，應考慮兩顆衛星的軌道特性、軌道測量和控制精度、允許控制頻度(間隔多少天作一次東西保持控制、南北控制次數/年)、推進劑消耗量、控制策略修改限制及可擴展性、定點保持精度等主要因素[4]。

當兩顆星在法向距離相等時，徑向距離差可以表示成：

Δr=(a1-a2)?asΔecos (φi-φe)

(1)

式中，φe、φi分別為相對偏心率矢量和相對傾角矢量的幅角；Δe為相對偏心率矢量的幅值；a1、a2、as分別為兩顆星的半長軸和同步軌道的地心距。

此時聯合隔離的條件可以表示成：

|Δr|=|asΔecos(φi-φe)|-|Δa|>d

(2)

式中，d為兩星的徑向隔離距離(約2 km)，Δa為兩顆星的半長軸之差。由于兩顆衛星南北方向控制策略和東西方向策略不相同，相對傾角矢量的幅角變化很大，因此只能適當增大相對傾角矢量和偏心率矢量的幅值，以滿足聯合隔離的條件。

3 偏心率矢量和傾角矢量聯合控制策略

3.1 傾角矢量控制策略設計

A星和B星的傾角矢量控制策略設計包括各自的傾角矢量初值控制、南北控制方向及傾角矢量控制等。A星在傾角矢量初值控制時，需要適當調整傾角控制時間，將傾角矢量控制到(-0.16°,-0.07°)附近。每次南北控制的傾角控制方向為

(3)

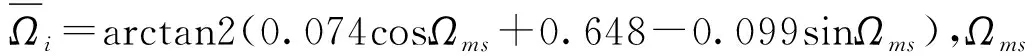
若控制前的傾角矢量為(ix,iy)，則傾角矢量控制目標為

iyT=-0.07°

(4)

根據偏心率矢量和傾角矢量聯合隔離的要求，B星傾角矢量控制要求為

ix>-0.02°

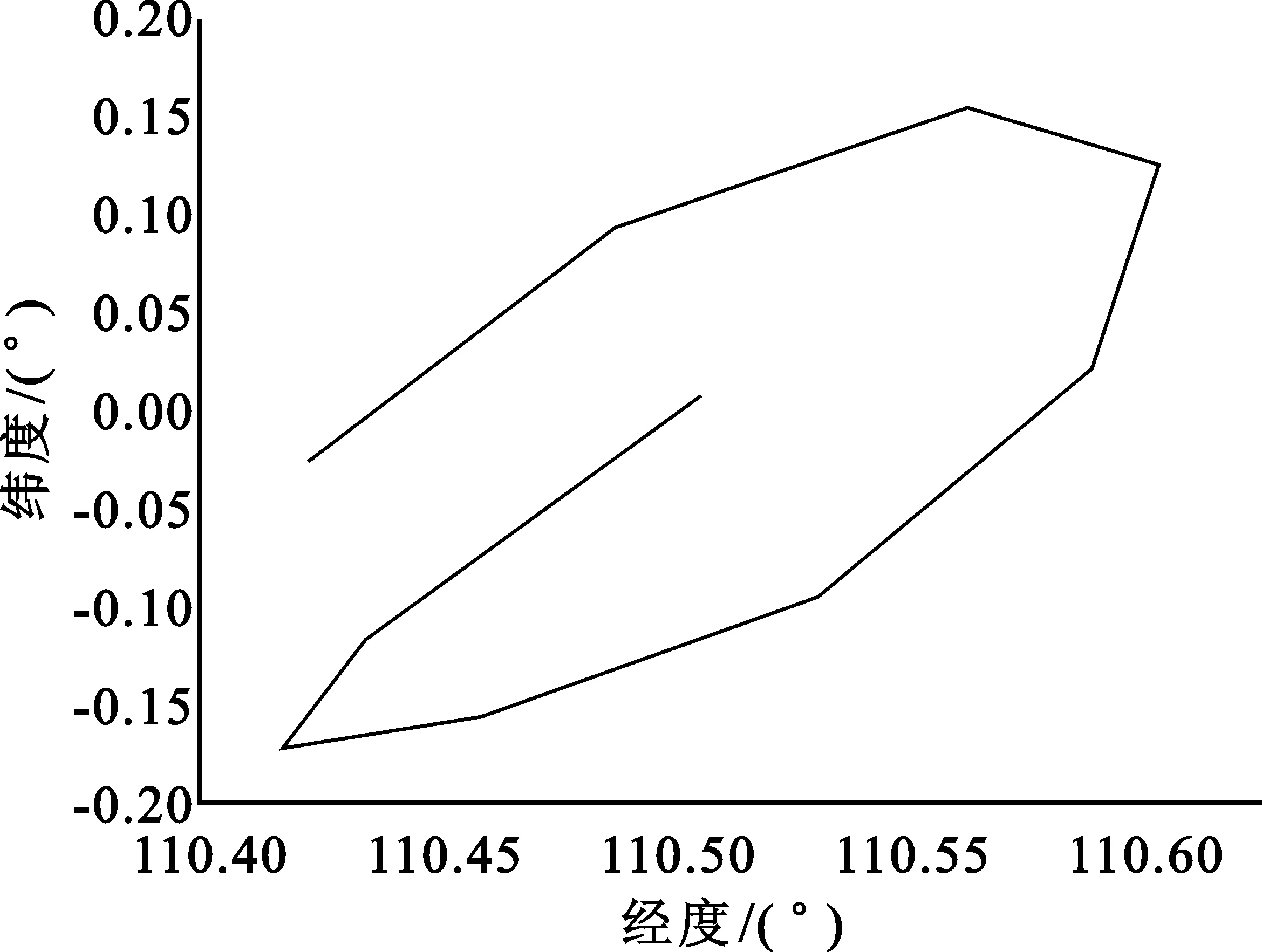
-0.1°

B星每次南北控制的傾角控制方向與A星的傾角控制方向相同，即：

B星若兩個月不進行南北控制，傾角必然超過0.1°，在這種情況下可以每年進行2次或4次非最優時刻的南北控制，以提高南北控制精度。

3.2 偏心率矢量控制策略設計

根據上面的聯合隔離參數，A星和B星共軌運行期間，希望兩星的偏心率矢量沿某一特定的圓軌跡變化。但當偏心率初值不同時，偏心率攝動圓就不同。日月引力、地球非球形攝動、太陽光壓會引起偏心率矢量周期性變化。另外，衛星東西位置保持和南北位置保持引起的東西耦合都會導致偏心率矢量變化。因此，相對偏心率矢量控制策略包括兩顆衛星的偏心率矢量初值設置、東西位置保持過程中的偏心率矢量控制策略和南北位置保持后的偏心率矢量控制策略。 A星需要將平偏心率矢量控制到：

eBx=eBxc+ec2cos (αs-β)

eBy=eBxc+ec2sin (αs-β)

(5)

式中，ec2=2.9×10-4為偏心率控后圓半徑，αs為當天的太陽赤經，β=23°為偏心率矢量遲后太陽方向的角度。平偏心率矢量不包含各種日周期項和月亮引力引起的半月周期項。在正常情況下，偏心率矢量控制通過東西控制實現，傳統的偏心率矢量控制采用雙脈沖控制。為了減少東西控制量產生的總控制誤差，因此偏心率矢量控制由雙脈沖控制改為單脈沖控制。實際控制時，需要對計算出來的控制時刻進行限制，于是采用如下限制策略：

若L-αs>360°，則L取L-360°；

若L-αs<180°，則L取L+360°；

若L-αs>165°，則L=αs+165°。

(6)

當A星南北位置保持時對東西位置保持耦合影響比較大，可能需要進行多次東西位置控制，修正衛星的平經度漂移率和星下點位置以及控制衛星的偏心率矢量，此時偏心率矢量的控制目標同偏心率矢量初值設置。

為了適當提高兩顆星的徑向隔離距離，要求B星偏心率矢量控制時，適當考慮傾角的影響。根據前面的隔離原則，B星的偏心率矢量應滿足如下條件：

(7)

式中，ec=0.000 27為偏心率控制圓半徑，β1=25°，Ki=0.000 5為傾角矢量對偏心率控制的影響因子。當B星的偏心率矢量的攝動圓半徑為4.5×10-4，向西控制的標稱時刻遲后太陽赤經75°左右，于是采用如下限制策略：

若L-αs>165°，則L=αs+165°

(8)

4 衛星定軌方法和實施策略

為了實時監測在軌衛星的軌道位置用以評估雙星定位的實施效果，需要利用衛星地面控制系統的多個地面標校站作為測軌站對衛星進行實時測軌。根據定軌幾何需求，可利用分布于國內東部、西部和南部的多個測軌站對A星和B星進行實時測軌。平時，測軌站數據入站頻率為5秒/次；衛星軌位保持期間，多個測軌站的測軌數據采樣率可提高至1秒/次，可為測軌計算提供相當于平時5倍的測軌數據，以保證軌控期間衛星軌道計算精度。

在對A星和B星進行測軌時采用了3種不同的定軌計算方法：三站交匯的幾何定軌法、兩個站以上的卡爾曼濾波法和最小二乘法。幾何定軌法是利用3個以上的已知點的觀測，根據衛星和測站的幾何關系，解算衛星觀測瞬間的位置坐標。由于幾何法可用來實時提供衛星的位置，因此在對衛星軌控期間，可以利用幾何法實時計算衛星的軌道和預報短時間內的星歷。卡爾曼濾波法即利用兩個以上測軌站跟蹤數據確定衛星軌道，該方法得到一組測距量，就完成一次軌道確定，適用于一個特定的測量周期內。根據卡爾曼濾波法的特點，在對衛星軌控前調整測軌站采樣頻率，輸入衛星機動文件(時間、推力和推力方向)和衛星姿態及面質比，即可提供衛星的星歷。卡爾曼濾波法和幾何法在軌控期間并用，經軌道精度評估后選優。最小二乘法是用使衛星軌道的計算觀測量和實際觀測量的差的平方和最小的辦法來確定衛星某歷元時刻的位置速度與攝動(地球非球形引力場攝動、日月引力攝動、太陽光壓攝動、潮汐攝動)模型參數。最小二乘法用于衛星軌控前和軌控后日常運行中的星歷預報。系統根據衛星位置保持期間的不同狀態分別采用幾何法、卡爾曼濾波法和最小二乘法按照一定的策略完成衛星軌道計算。日常運行中，采用最小二乘法進行星歷預報；軌道控制期間，采用幾何法或卡爾曼濾波法實時計算星歷，以保障軌控期間軌位計算精度。

5 衛星共位效果評估

為了直觀體現雙星共位的效果，可以利用雙星共位運行后其中一顆衛星的星下點軌跡來表示。如果衛星星下點軌跡在位置保持控制精度范圍內，即可表示衛星在正常軌道范圍內運行。當兩顆衛星都在保持相對距離不變的正常軌道范圍內運行時，即可實現雙星共位穩定運行。以A星為例，在共位試驗中，其南北位置保持控制頻度由三個月改為兩個月；東西位置保持控制頻度為半個月或一個月。A星在南北位置保持控制期間星歷變化如圖1和圖2所示。圖1表示第1次南北軌道控制期間的衛星星下點軌跡。由此可看出本次南北位置保持控制期間，衛星經緯度漂移范圍是：東西方向為-0.08°～0.10°，南北方向為-0.17°～0.16°。圖2表示最后1次南北軌道控制期間的衛星星下點軌跡。由此可看出本次南北位置保持控制期間，衛星經緯度漂移范圍是：東西方向為-0.08°～0.11°，南北方向為-0.06°～0.14°。

圖1 第1次南北位置保持期間衛星星下點軌跡

圖2 最后1次南北位置保持期間衛星星下點軌跡

A星在東西位置保持控制期間星歷變化如圖3和圖4所示。圖3表示A星在共10余次東西軌道控制期間的某一次東西位置保持后的衛星星下點軌跡。由此可看出此次東西位置保持控制期間，衛星經緯度漂移范圍是： 東西方向為-0.16°～0.13°，南北方向為-0.16°～0.17°。圖4表示A星最后一次東西位置保持后的衛星星下點軌跡。由此可看出此次東西位置保持控制期間，衛星經緯度漂移范圍是： 東西方向為-0.132°～0.034°，南北方向為-0.116°～0.117°。

圖3 南北位置保持期間衛星星下點軌跡1

圖4 南北位置保持期間衛星星下點軌跡2

綜上所述，在近1年的雙星共位試驗中，A星的位置保持精度為東西方向優于±0.1°，南北方向優于±0.18°，滿足B星東西方向優于±0.1°、南北方向優于±0.2°的精度要求。因此，無論是衛星南北位置保持后的衛星軌道還是東西位置保持后的衛星軌道都能證明衛星的位置精度滿足雙星共位要求，即利用偏心率矢量和傾角矢量聯合隔離的方法能夠有效地實現雙星共位。

6 結束語

本文對偏心率矢量和傾角矢量聯合隔離法進行雙星定位的工程實踐進行了詳細論述，探討了如何利用該方法制定合理可行的衛星軌位控制策略，并通過有效的衛星定軌方法進行雙星共位效果評估。通過雙星共位效果可以證明利用該方法制定的衛星軌位控制策略的有效性。雙星共位的成功實踐證明我國衛星共位技術已經從理論成果推進到了工程實踐，今后將會有越來越多的衛星實現共位運行。衛星共位技術能夠提升我國的衛星軌道控制能力，并為我國爭取到更多的衛星軌道資源。

參考文獻：

[1] 石善斌,董光亮,羅強.兩種靜止軌道多星共位位置保持策略比較[J].上海航天,2009,26(2):55-60,64.

SHI Shan-bin,DONG Guang-liang,LUO Qiang. The Comparison of Two Station-Keeping Strategies for Collocation of Geostationary Satellites[J]. Aerospace Shanghai, 2009,26(2)：55-60, 64.(in Chinese)

[2] 李建成,袁勇,王西京,等.基于絕對偏心率隔離的一點雙星共位實現[J].西北工業大學學報,2006,24(1):1-4.

LI Jian-cheng,YUAN Yong,WANG Xi-jing,et al. A Method of Collocating Two Chinese Geostationary Satellites with Two Eccentricity Vectors[J]. Journal of Northwestern Polyechical University, 2006,24(1)：1-4.(in Chinese)

[3] 張曉欣. 共位衛星距離分析[J]. 無線電工程, 2007, 37(12):43-45,48.

ZHANG Xiao-xin. Distance Analyze of Common Orbit Satellite[J]. Radio Engineering of China,2007,37(12)：43-45, 48.(in Chinese)

[4] 戴光明, 王茂才. 多目標優化算法及在衛星星座設計中的應用[M]. 武漢：中國地質大學出版社, 2009.

DAI Guang-ming,WANG Mao-cai. Multi-Objective Optimization Algorithms and its Application in Satellite Constellation Design[M]. Wuhan: Chinese Geology University Publishing House, 2009.(in Chinese)