圖的反符號星k控制數

徐保根，孔祥陽，陳悅

(華東交通大學基礎科學學院，江西南昌330013)

圖的反符號星k控制數

徐保根，孔祥陽，陳悅

(華東交通大學基礎科學學院，江西南昌330013)

反符號星k控制函數;反符號星k控制數;反符號星控制函數;反符號星控制數

在1998年美國圖論學者W T Haynes等人出版了專著，該著作較為全面而又系統地總結了近些年在圖論方面的一些重要研究成果。但這些成果幾乎都是關于圖的點控制問題，與圖的邊控制問題相關的結果卻比較少。為了將圖的控制理論內容進行進一步健全和豐富，我們將由對圖的點控制問題的研究轉向對圖的邊控制問題的研究，我們已經得到了一些研究成果，例如，符號邊控制，符號星控制和符號圈控制等。在本文中，我們將引入一個新概念，即圖的反符號星k控制概念。

本文所考察的圖均為無向簡單圖，文中的符號和術語若無特別說明則均與文獻相同。

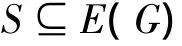
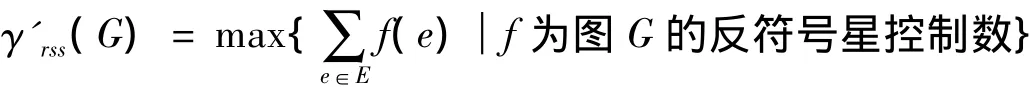
下面我們將圖的反符號星控制概念進行推廣，從而引入一種新的圖的邊控制概念。

對于空圖，所以反符號星k控制概念既是對反符號星控制概念的一種推廣，也是對符號星k控制概念的一種推廣。關于圖的反符號星控制數，文［6］中指給出了如下結果:

本文在對文［7］中的結果進行了推廣——給出了一般圖的反符號星k控制數的若干上界，在此基礎上，給出了n階路Pn和n階圈Cn的反符號星k控制數的表達式。

定理1對于任意n階圖G，當δ≥1，1≤k≤n－1時，有

其中:δ=δ(G)，Δ=Δ(G)分別表示圖G的最小度和最大度。

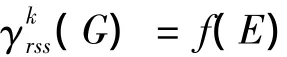
其中:δ=δ(G)和Δ=Δ(G)分別為圖G的最小度和最大度。

另外，我們還可得到

可見結論是成立的，定理證畢。

根據定理2，我們可得到如下推論:

推論對任意n階r－正則圖G，若r≥1，且1≤k≤n，則有

最后我們給出n階路Pn和n階圈Cn的反符號星k控制數的表達式。

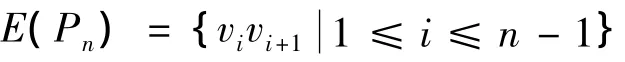
可以驗證:f為Pn的一個反符號星k控制函數且有

結合(3)知結論(Ⅰ)成立。同理可知結論(Ⅱ)也成立，定理證畢。

［1］HAYNES T W，HEDETNIEMI S T，SLATER P J.Domination in graphs［M］.New York:Marcel Dekker，INC，1998.

［2］XU BAOGEN.On signed edge domination numbers of graphs［J］.Discrete Math，2001，239(1/2/3):179－189.

［3］XU BAOGEN.Two classes of edge domination in graphs［J］.Discrete Appl Math，2006，154(10):1 541－1 546.

［4］XU BAOGEN.On signed cycle domination in graphs［J］.Discrete Math，2009，309(4):1 007－1 012.

［5］BONDY J A，MURTY V S R.Graph Theory with Applications［M］.Elsevier，Amsterdam，1976.

［6］趙華，徐保根，趙金鳳，帥春萍.關于圖的反符號星控制數［J］.華東交通大學學報，2008，25(5):84－87.

［7］徐保根，李春華.圖的符號星k控制數［J］.純粹數學與應用數學，2009，25(4):638－641.

(責任編輯 王建華)

Reverse Signed Star k－subdomination Numbers of Graphs

Xu Baogen，Kong Xiangyang，Chen Yue

(School ofBasic Sciences，East China Jiaotong University，Nanchang 330013，China)

signed star k－dominating function;signed star k－domination number;signed star dominating function;signed star domination number

O157.5

A

1005－0523(2010)04－0068－03

2010－04－25

國家自然科學基金項目(10661007);江西省教育廳科研項目(GJJ09215)

徐保根(1963－)，男，教授，研究方向為圖論與組合數學。