基于組合優化方法的平面葉柵優化設計

朱國俊，羅興锜，郭鵬程，戴辰辰

（西安理工大學水利水電學院，西安 710048)

基于組合優化方法的平面葉柵優化設計

朱國俊，羅興锜，郭鵬程，戴辰辰

（西安理工大學水利水電學院，西安 710048)

采用奇點分布法與貝塞爾(Bezier)曲線參數化方法相結合的平面葉柵設計方法進行葉柵的初步設計與參數化表達。該方法在完成設計的同時為基于現代優化算法的葉柵粘性流動最優化設計提供設計變量，以實現葉柵翼型的變形控制。然后結合N-S方程流場數值模擬，采用多目標遺傳算法(NCGA)和序列二次規劃法(NLPQL)組合的優化算法，通過調節葉柵翼型的形狀控制參數對葉柵的總壓損失和空化性能進行了優化。結果表明，優化效果良好。

貝塞爾曲線; 平面葉柵；優化設計; 多目標遺傳算法; 序列二次規劃法

1 引言

水輪機的性能在很大程度上決定了整個電站的經濟效益，而轉輪作為整個水輪機的核心部件，其工作性能又影響著整個水輪機組的優劣，因此，轉輪的設計及其優化在水輪機改進和提高的過程中具有不可替代的重要地位。

長期以來，人們力圖通過理論計算設計出優良的轉輪，但轉輪內部的流動規律極為復雜，其流動參數和幾何參數之間的關系也難以確定，所以試驗技術和CFD數值模擬技術在轉輪性能的改善過程中處于絕對地位。而由于試驗需要耗費大量的資金和時間，因此，“初始設計→CFD數值模擬→修改設計”的方法更被國內各大廠家所青睞。但是在“修改設計”這一步多靠人工經驗，缺乏計算機輔助優化，這也導致了該方法的設計周期變長。

近年來國內外流行的優化設計方法提供了新的葉片設計思路，即先通過初始設計方法設計出葉片的幾何形狀，然后將其表達成設計參數，而性能則表達成隨設計參數變化的目標函數。所以優化設計過程就是根據目標函數，選擇設計參數使得性能最佳。該過程是一個自動化的過程，無需人工干預，因此，大大縮短了設計周期。

本文根據上述新的葉片優化設計思路，開發了基于奇點分布法和貝塞爾（Bezier）曲線參數造型方法的軸流式水輪機平面葉柵設計方法，并通過多目標遺傳算法（NCGA）和序列二次規劃法（NLPQL）相結合的組合優化方法對生成的平面葉柵翼型進行了優化。

2 平面葉柵的設計與參數化

葉柵的設計方法是先采用奇點分布法設計出翼型骨線并將骨線用Bezier曲線參數化，這樣可以通過控制參數的變化來變化骨線形狀。然后把優秀翼型的厚度疊加到骨線上，這樣就形成了通過控制參數的變化來變化葉柵翼型。

奇點分布法是在假定來流為無旋有勢流動、葉片無限薄的前提下用一系列分布在翼型骨線上的奇點來代替葉柵中的翼型對水流的作用，這些奇點是一系列的源、匯和旋渦，原來翼型圍成線的位置是流線。只要恰當地選擇奇點的分布規律，就可以使奇點和來流所造成的流場和原來葉柵繞流的流場完全相同。因此，葉柵繞流的計算就可轉化為基本勢流的疊加計算。

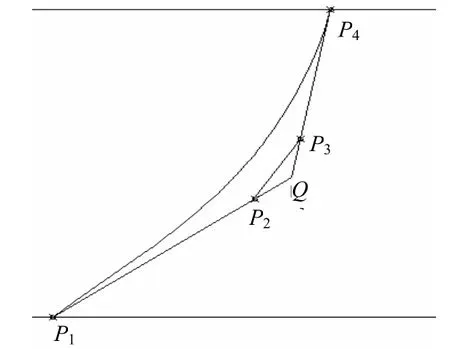
圖1 骨線參數定義

采用奇點分布法設計出骨線后，用三次Bezier曲線將其參數化為P1、P2、P3、P4四個控制參數。其中，保持P1、P4的切線方向不變，Q為始末點P1、P4切線的交點，如圖1所示。根據Bezier曲線的性質，控制點P2、P3將在直線P1Q和P4Q上變化，令P2＝P1+C1×（Q－P1），P3＝P4－C2×（P4－Q），C1、C2為小于1的系數。給定 C1、C2的大小，則可以確定控制點P2、P3。這樣，根據P1、P2、P3、P4四個控制參數就可以得出骨線形狀，然后通過加厚程序將優秀翼型的厚度分布疊加到骨線上就得出有厚翼型，如圖2所示。這樣，就可以通過控制C1、C2兩個參數來控制翼型的變化。因此，在優化過程中，只要對C1、C2兩個參數進行控制，就可以實現對翼型的控制。

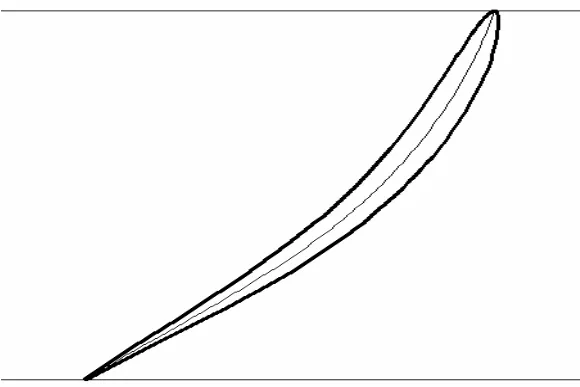
圖2 套加到骨線上的有厚翼型

3 流場分析

3.1 網格劃分

取兩個翼型間的通道進行葉柵流場分析，流場計算網格采用六面體的結構化網格，單周期通道網格拓撲結構如圖3，計算網格如圖4，網格數為80×40。

在優化的過程中，葉柵翼型是在不斷變化的，所以，計算網格也需要隨著翼型的變化而不斷調整，為此，采用程序將相同的網格拓撲結構應用到不同的翼型通道上，并讓其自動映射，即可實現網格的調整。

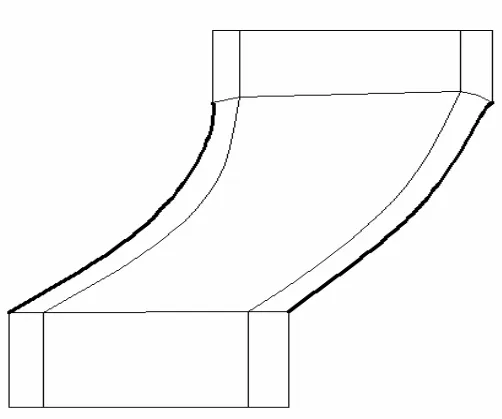
圖3 計算網格拓撲

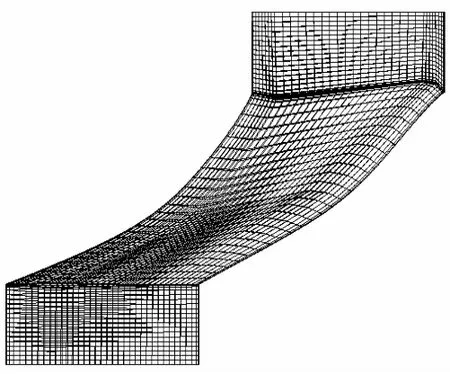
圖4 計算網格

3.2 控制方程求解

平均化Navier-Stokes 如下：

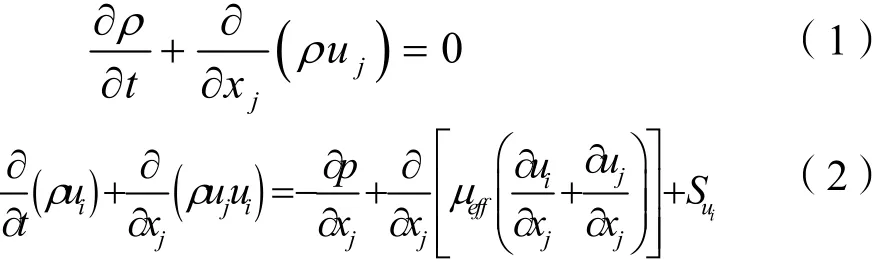
這里采用商業CFD軟件CFX11提供的不可壓縮時均化3D Navier-Stokes方程。通過標準k－ε雙方程湍流模型來封閉N-S方程組，并在近壁區采用壁面函數法求解流場。然后根據流場計算結果得出翼型通道損失和翼型上的最低壓力。

3.3 邊界條件

給定適當的邊界條件對于流場計算是很重要的。在優化過程的流場計算中，進口給定流速條件，出口給定靜壓條件，固體壁面采用無滑移邊界條件，即Uwall=0。

4 優化方法

在葉柵翼型優化問題中，以C1、C2兩個翼型控制參數作為設計參數，以葉柵損失和翼型上的最低壓力值作為優化目標，進行多目標優化。

優化問題可以表述如下：

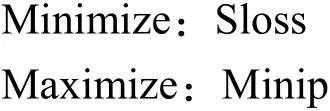
目標函數約束：

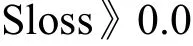
設計變量約束：

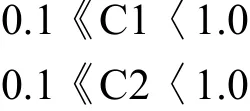
式中：Sloss為葉柵通道的損失，Minip為在翼型上最低壓力值。

圖5 優化流程

由于描述轉輪內部流動的N-S方程組是復雜的非線性方程組，目標函數與設計參數之間呈高度非線性關系，存在很多局部極值點，這就會使在尋優過程中出現局部最優解。為了避免最后產生局部最優解，先采用多目標遺傳算法（NCGA）進行整體尋優，然后采用序列二次規劃法（NLPQL）加快收斂速度，從而快速尋出最優解。

多目標遺傳算法 NCGA中采用二進制的編碼方式，并采用單點交叉和基本位變異來進行交叉和變異操作。它與標準遺傳算法GA不同的地方就在于進行交叉操作時，不是在種群個體中兩兩隨機配對進行，而是在具有一定程度的類似性的個體之間進行，也就是說在進行交叉操作時，將適應值接近的個體放在一塊進行交叉，旨在提高其探索性。

在本次優化中，先采用多目標遺傳算法NCGA對整個解空間進行全局搜索，使解收斂到最優解附近，然后再采用序列二次規劃法以 NCGA算法的收斂解作為起始點進行局部搜索。采用這種組合優化方法是因為遺傳算法的局部搜索能力不強，盡管它搜索到了全局最優解附近，但要達到最優解是要花費較大代價的，因此，在局部搜索時，采用穩定性良好的數值優化方法——序列二次規劃法來進行搜索，這樣既能避免陷入局部最優，又能加快收斂的速度。優化流程如圖5所示，整個優化過程全部由計算機仿真完成，不需要進行干預。

5 算例及分析

以 ZZ440軸流式水輪機為研究對象，對半徑為0.8R1處的平面葉柵進行優化設計。表1和表2給出了設計的參數。

表1 基本參數

表2 給定設計參數

通過上述參數，可以直接得出或間接給出計算所需參數。然后采用編制的結合了Bezier曲線參數化的奇點分布法程序，在設計工況下計算出半徑為 0.8R1處的平面葉柵初始翼型并將其參數化，然后取該翼型控制參數C1、C2作為設計參數進行優化。優化前后的設計變量見表3，優化的結果見表4。

采用的多目標遺傳算法的交叉概率為0.8，變異概率為0.01，代數為25代。由于設計變量較少，因此，每代的種群數取12。在優化了310步后得出最優結果。

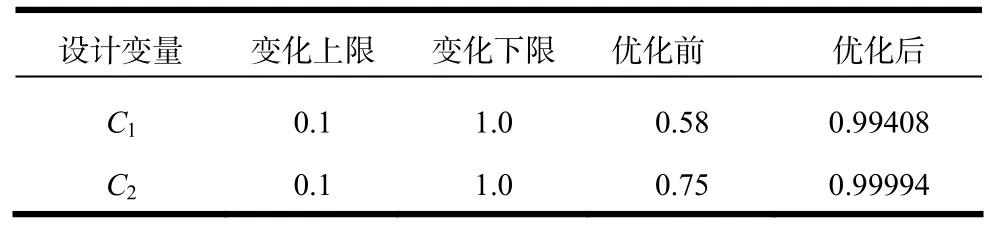
表3 設計變量

表4 優化結果

由表3和表4可知，經過多目標優化后，葉柵的損失下降了17.6%，葉柵翼型上的最低壓力值上升了38.69%。也就是說在優化后，不僅提高了葉柵效率，而且葉柵的空化性能也有了很大的改善。優化前后的翼型見圖 6，其中實線為原始翼型，虛線為優化后的翼型。優化前后翼型上的靜壓分布見圖 7。由圖中可以看出，優化后翼型上的壓力比優化前整體有所抬升，翼型背面最低壓力值升高。

圖6 優化前后翼型對比

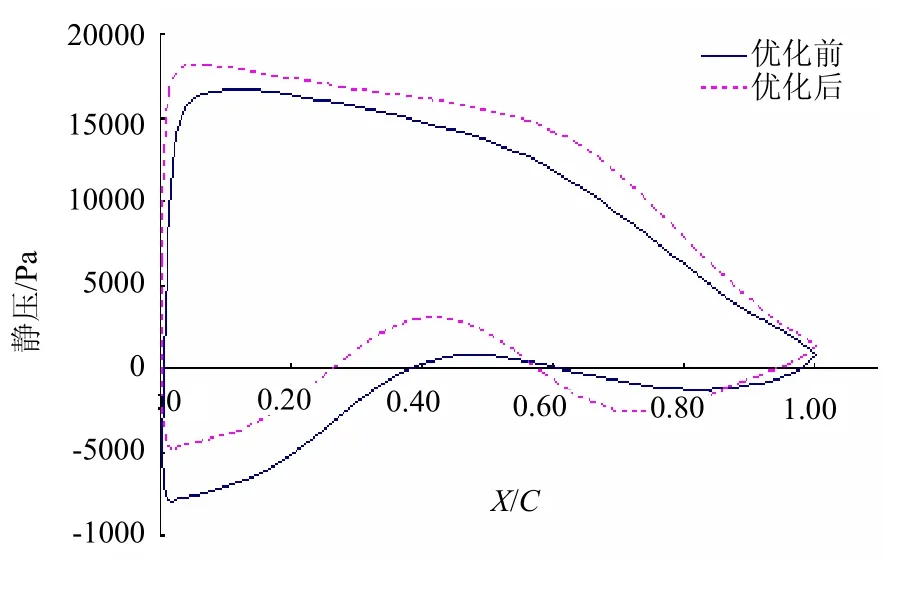
圖7 優化前后翼型上的靜壓分布

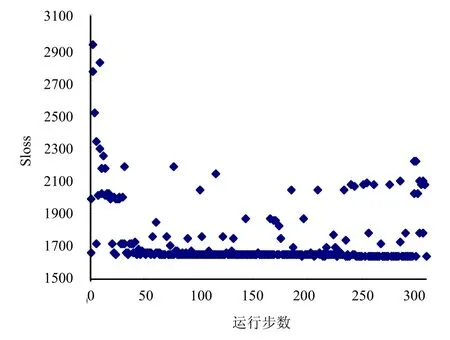
圖8 Sloss的優化歷史

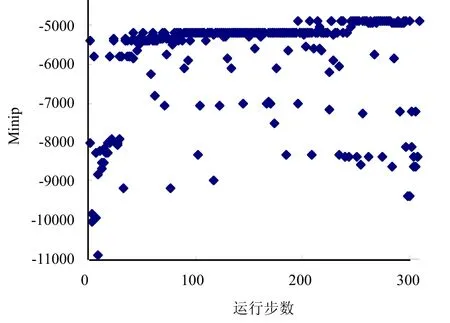
圖9 Minip的優化歷史

圖8和圖9給出了Sloss和Minip兩個目標函數的優化歷史圖，從圖中可以看出，目標函數的優化效果和算法的收斂趨勢良好。

6 結論

（1）采用奇點分布法和貝塞爾（Bezier）曲線參數造型方法的軸流式水輪機平面葉柵設計方法簡便快捷，能把設計出來的葉柵翼型快速參數化，以供優化模塊調用。

（2）采用多目標遺傳算法(NCGA)和序列二次規劃法(NLPQL)相結合的組合優化方法對生成的平面葉柵翼型進行了優化，避免了局部最優解。在優化后葉柵損失和空化性能大幅度提高，很好地達到了優化的效果。

（3）針對水輪機的運行特點，以損失和空化性能作為優化目標進行優化，整個優化過程全部由計算機完成，無需進行干預，因此，達到了自動優化的目的。

[1] Tomas L, Pedretti C, Chiappa T. Automated design of a Francis turbine runner using global optimization algorithms[C]. Proceeding of the XXI IAHR Symposium on Hydraulic Machinery and Systems,Switzerland，2002.

[2] R Schilling, S Thum, N Muller. Design optimization of hydraulic machinery bladings by multi level CFD technique[C]. Proceeding of the XXI IAHR Symposium on Hydraulic Machinery and Systems,Switzerland，2002.

[3] 郭鵬程, 羅興锜, 劉勝柱. 基于三維紊流數值計算的離心泵葉輪優化設計[J]. 機械工程學報,2004, 40(4): 181-184.

[4] 陳波, 袁新. 基于NURBS三維造型的粘性氣動最優化技術[J]. 工程熱物理學報, 2005, 26(5):764-767.

[5] 羅興锜. 水力機械轉輪現代設計理論及應用[M].西安: 西安交通大學出版社, 1997.

羅興锜（1962-），1995年畢業于清華大學水利系，博士，主要從事水力機械技術研究工作，教授。

2D Cascade Optimization Design Based on Parametric Bezier Curve

ZHU Guo-jun, LUO Xing-qi, GUO Peng-cheng, DAI Chen-chen
(Faculty of Water Resources and Hydraulic Power, Xi' an University of Technology, Xi’an 710048, China)

Use the method which combined singularities method with parametric method of Bezier curve to design and represent initial 2D cascade. This method provides 2D cascade optimization designs based on modern optimization tools with design variables at the time which design was completed, so it could achieve the deformation of airfoil. Use the Navier-Stokes equation to carry out the numerical simulation of viscous flow in cascade. The optimization algorithm which combined Multi-objective Genetic Algorithm(NCGA) with NLPQL algorithm was used for exploration. By modifying the shape parameters of cascade profile, the total pressure loss and suction performance were optimized. The results show that the method have good performance on optimization.

bezier curve; 2D cascade; optimization design; MOGA; NLPQL

TK730.2

A

1000-3983（2010）01-0050-04

國家自然科學基金重點項目(90410019)

2008-10-20

朱國俊（1984-），西安理工大學水利水電工程專業在讀研究生。