一個(3+1)維孤子方程的周期解＊

吳勇旗

(湛江師范學院數學與計算科學學院,湛江 524048)

一個(3+1)維孤子方程的周期解＊

吳勇旗?

(湛江師范學院數學與計算科學學院,湛江 524048)

(2009年3月6日收到;2009年4月14日收到修改稿)

利用Hirota方法及Riemann theta函數得到了一個(3+1)維孤子方程的周期解.在極限情況下,該周期解退化為孤子解.另外,利用計算機技術和Mathematica繪制了解的三維曲面圖.

Hirota方法,Riemann theta函數,(3+1)維孤子方程,周期解

PACC:0340K,0290

1.引言

過去幾十年,人們一直在努力探索非線性發展方程特別是孤子方程的求解方法,目前已經有了幾種有效的方法,如著名的反散射方法、B?cklund變換法、穿衣服方法、Painlevé展開法等等.最近,Lax對的非線性化方法[1—3]、齊次平衡法[4—7]、雙曲函數法[8—13]、Jacobi橢圓函數展開法[14]等也都被用來求非線性發展方程的各種顯式解.然而,尋找新形式的顯式解仍然是一件很有意義的工作.本文利用Hirota方法及Riemann theta函數[15—20]得到了一個(3 +1)維孤子方程的新的周期解.在極限情況下,該周期解退化為孤子解.另外,利用計算機技術和Mathematica繪制了解的三維曲面圖.

2.(3+1)維孤子方程與周期解

該方程與Ablowitz-Kaup-Newell-Segur(AK NS)譜問題密切相關,許多學者對此方程都做了大量的研究[21—23].文獻[21]通過AK NS方程組得到了該方程,它與一個(2+1)維破碎孤子方程[20,21]、一個具有三個位勢的耦合Kadometsev-Petviashvili(KP)方程有緊密的聯系(見文獻[21]及其參考文獻).文獻[21]的作者通過拉克斯對(Lax Pair)的非線性化方法并引入Abel-Jacobi坐標證明了方程(1)的Liouville完全可積性并得到了它的代數幾何解;文獻[22]利用Hirota方法及形式攝動得到了它的Wronskian形式解和N孤子解;文獻[23]通過雙線性B?cklund變換得到了它的多種孤子解和駐態有理解.本文則利用Hirota方法及Riemann theta函數得到了它的周期解.

2.1.Hirota雙線性算子的定義

由于這里涉及四個變量,我們定義Hirota雙線性算子為

其中,l,m,n,r都是非負整數,Hirota雙線性算子有許多重要的性質,這里用到的有

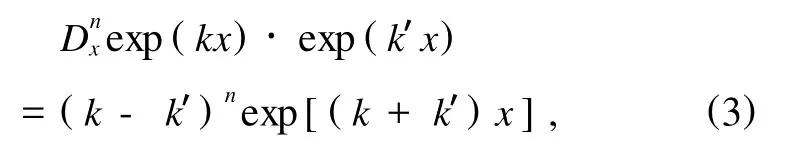
或者,更一般地,當F為一多項式函數時,有

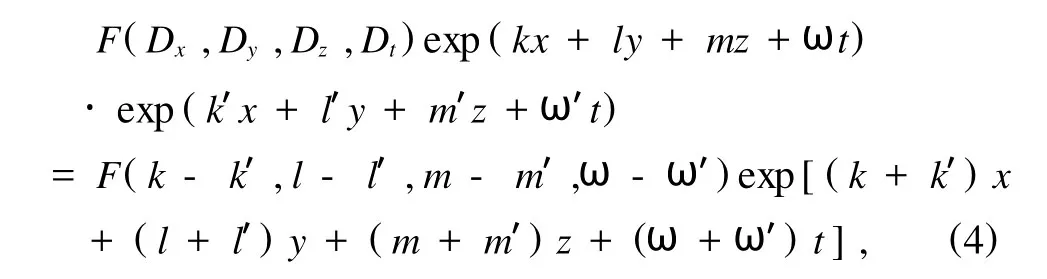
它們可以直接從定義出發得到.利用Hirota方法的關鍵是找相關變量變換,對于(3+1)維孤子方程(1)來說,我們取

本文研究一個(3+1)維孤子方程

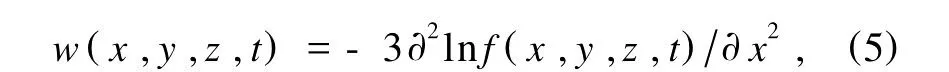
將(5)式代入(1)式并對x積分兩次,得到

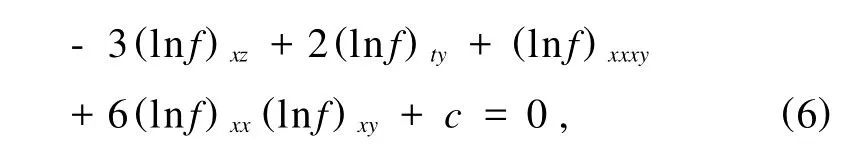
其中c為積分常數(c=c1(y,z,t)x+c2(y,z,t)),一般可以取為零,但是下面我們可以看到這里不可以取零.經過直接計算,有

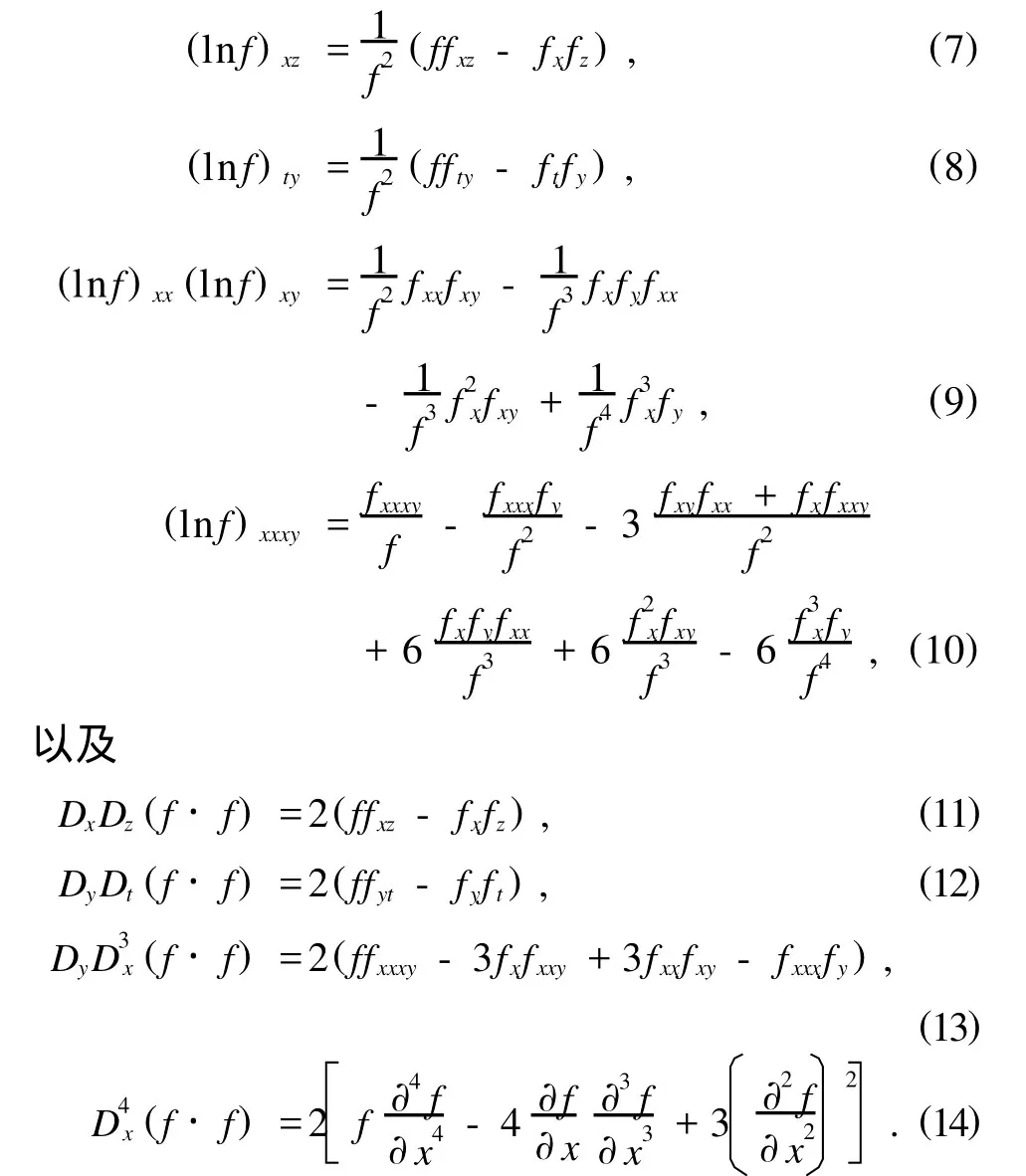
將(7)—(10)式代入(6)式并利用(11)—(14)式,便得到(3+1)維孤子方程(1)的雙線性形式為

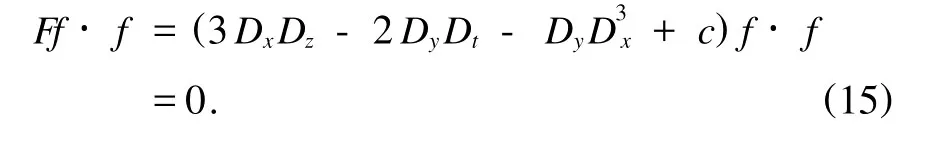
2.2.方程(1)的單周期解

為求得單周期波解,我們取一維Riemann theta函數[24]

其中,α,β,γ表示波數,ω表示頻率,η0是相常數,τ是一虛部大于零的復常數.把(16)式代入(15)式并利用(4)式,有

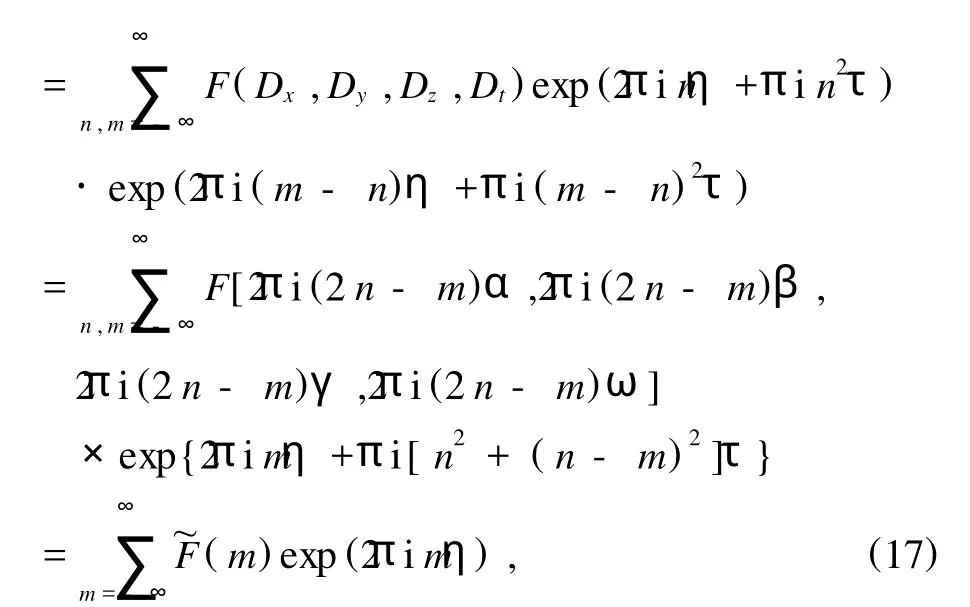
這里引入了求和指標m=n+n′,而~F(m)是

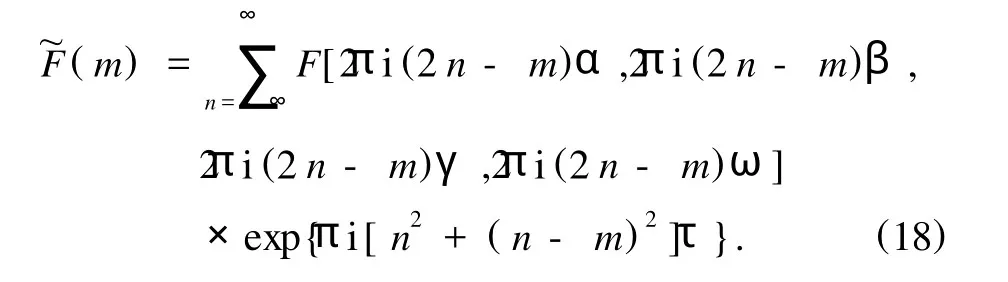
利用n=n′+1,(18)式變為

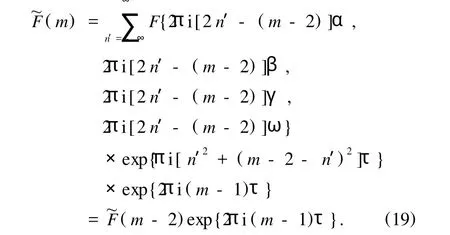
從(19)式我們可以看到,如果~F(0)和~F(1)都是零,那么所有的~F(m)均為零.另一方面,我們知道,即使其他的參數都知道,積分常數c和頻率ω卻是不知道的.因此,利用~F(0)=0和~F(1)=0解出積分常數c和非線性色散關系ω我們就可以得到方程(15)的精確周期解.~F(0)=0和~F(1)=0可以分別寫為

通過引入

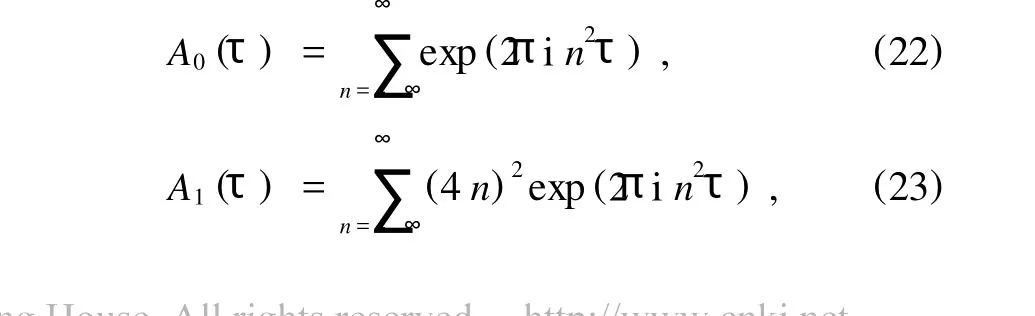
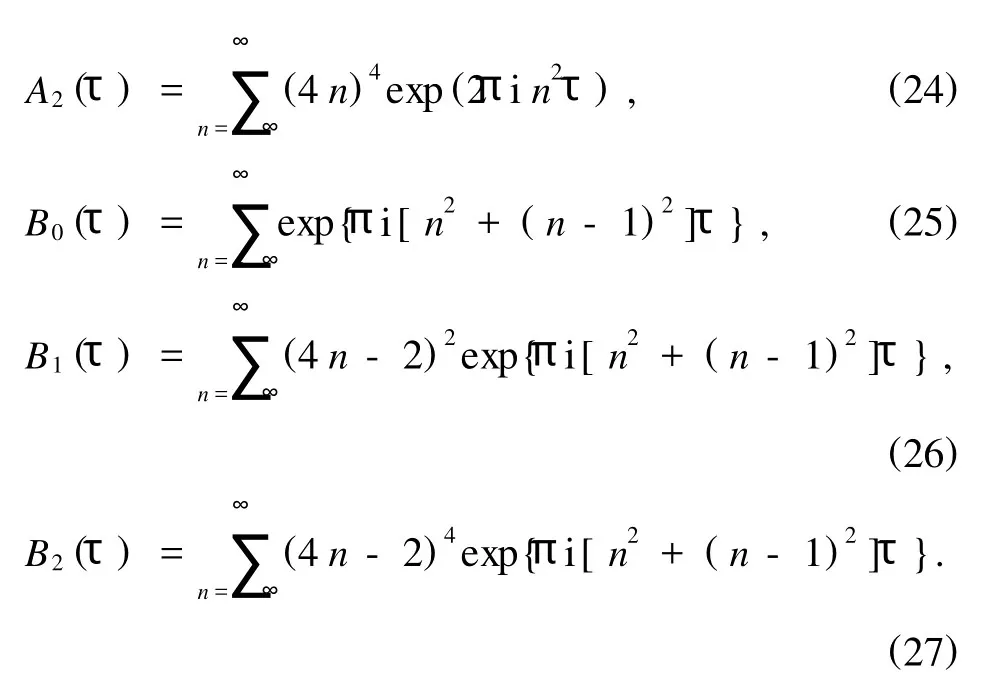
方程(20)和(21)可以寫為

解此方程組得到

因此,表達式(5)加上(16)和(30)式就是我們得到的(3+1)維孤子方程(1)的單周期波解(見圖1).

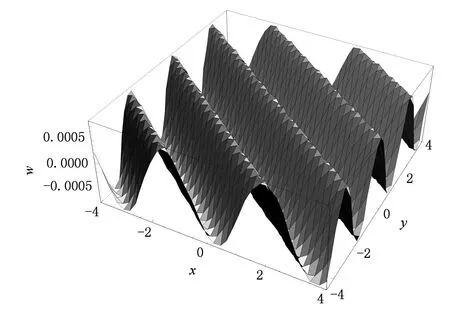
圖1

值得注意的是,在極限情況下,可以由周期解得到孤子解,為此我們引入

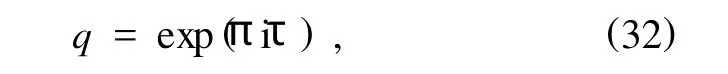
則(22)—(27)式及(30)式,(31)式可以分別表示為

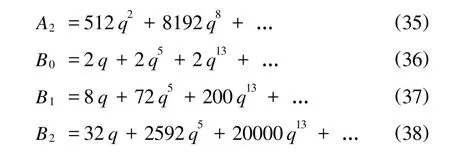
取極限q→0(或者lmτ→∞)有

引入記號

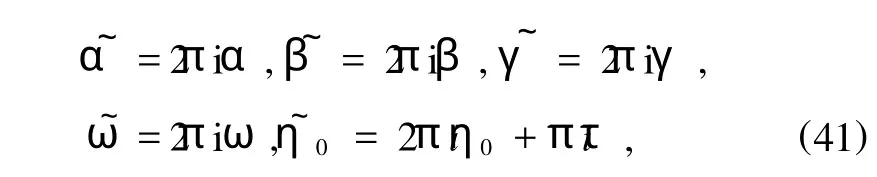
則在極限q→0(或者lmτ→∞)下,有

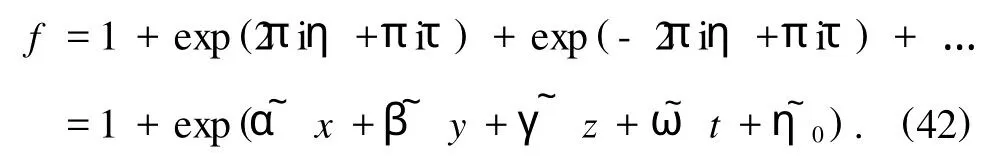
這是用雙線性變量表示的(3+1)維孤子方程(1)的解,通過(5)式,它可以轉化為孤子解

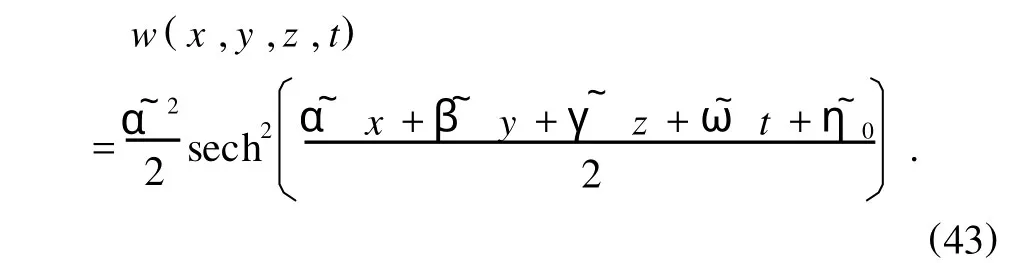
2.3.方程(1)的雙周期解

為求得雙周期波解,我們取N維Riemann theta函數

其中,αj,βj,γj,ωj和η0j的意義同一維情形相仿, τjk(j≠k)表示波之間的相互作用.并假設復矩陣τ =(τjk)N×N對稱且具有正定的虛部.把(44)式代入(15)式并利用(4)式,我們得到與(17)式相應的結果:

其中

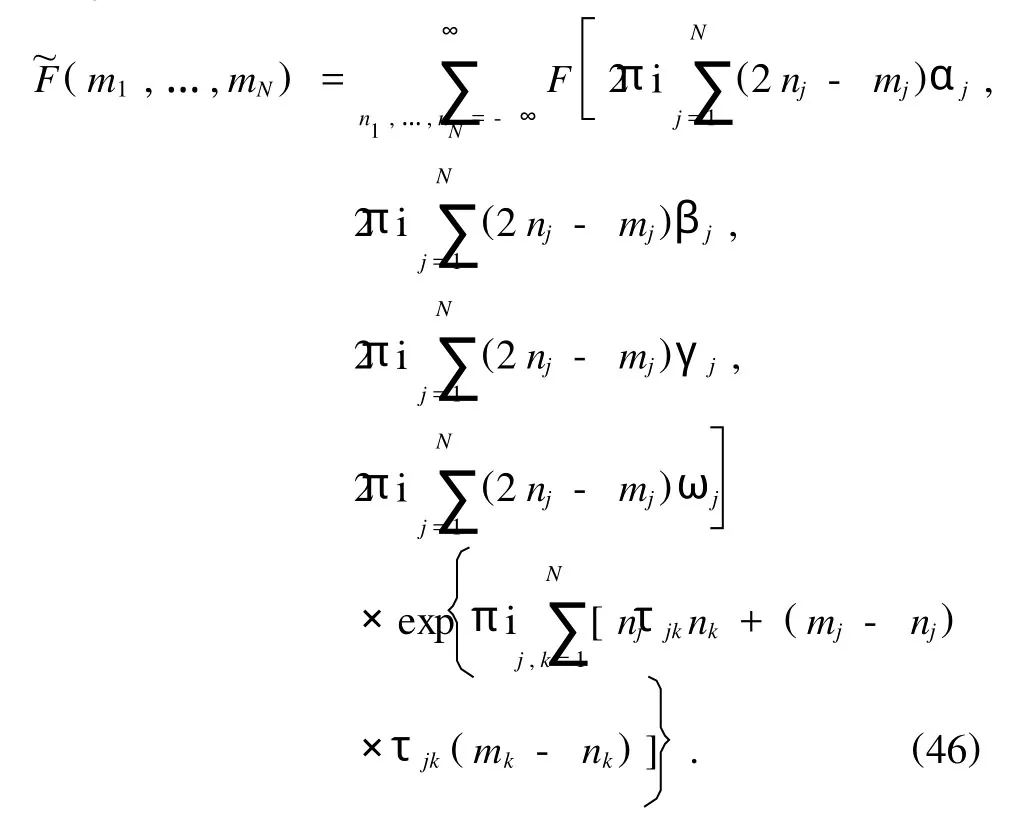
把第h個求和指標nh平移一個單位,我們得到與(19)式相對應的關系:

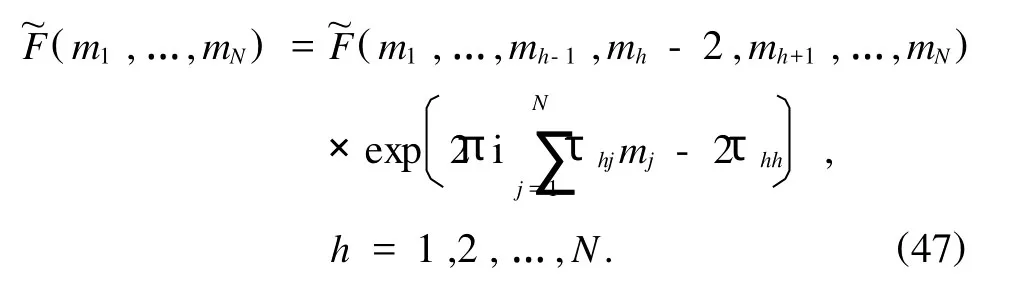
如果關系式

對所有的m1=0,1,m2=0,1,…,mN=0,1成立,那么(44)式便給出了(3+1)維孤子方程(1)的N周期波解.注意到(48)式共有2N個方程,而包含在問題中的未知量的個數包括積分常數c,非線性頻率ωj(j=1,…,N)和相互干擾項τjk(1≤j,k≤N,jN=1,2,方程個數與未知量個數相等,此乃意味著方程(1)總存在單周期波和雙周期波解.

下面就N=2時求(1)式的雙周期波解.由(47)和(48)式有

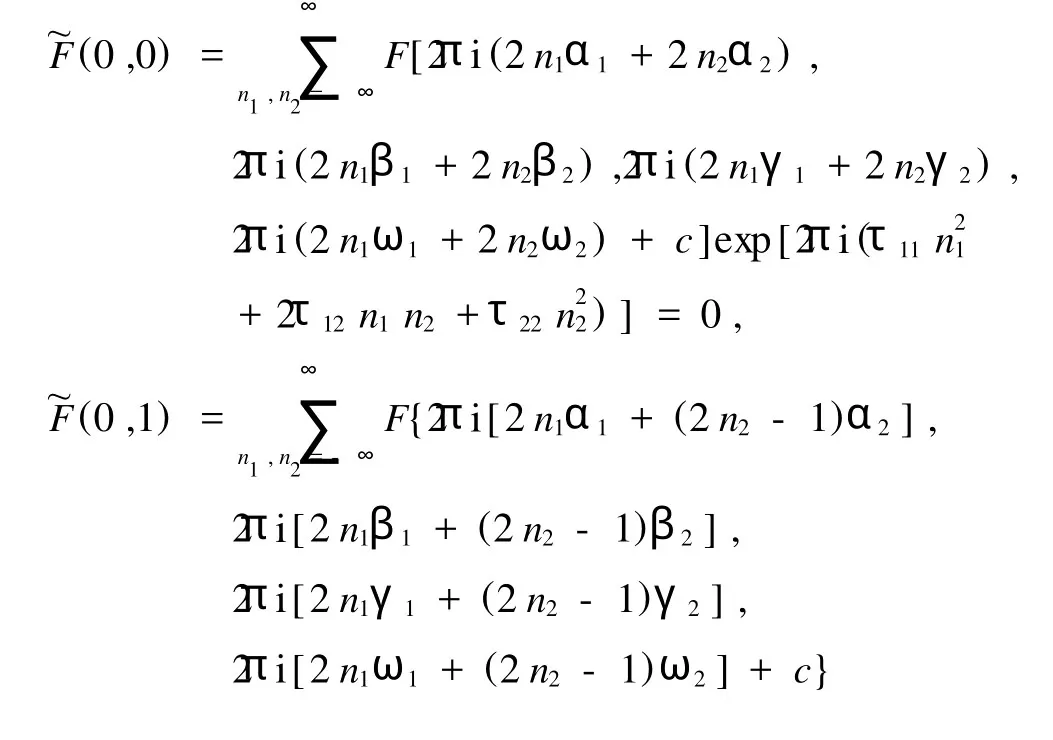
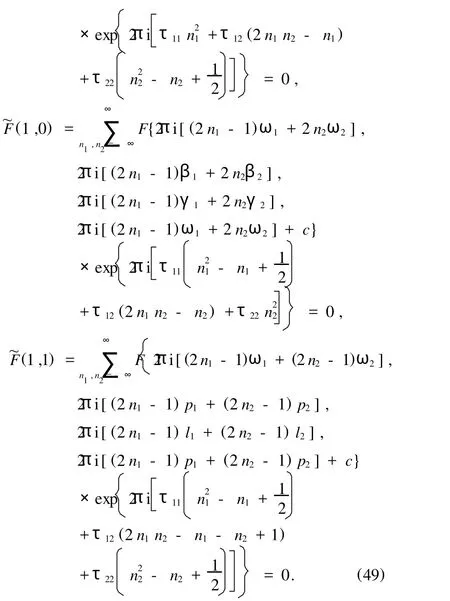
此方程組(49)確定了ω1,ω2,c和τ12.表達式(5), (44)(N=2)和(49)就是(3+1)維孤子方程(1)的雙周期波解.同樣值得注意的是,在極限情況下,也可以由周期解得到雙孤子解,為此我們引入記號

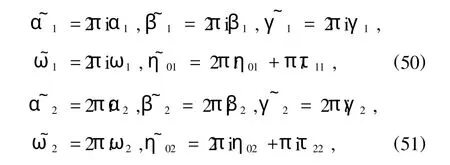
則當lmτ11→∞,lmτ22→∞時,有

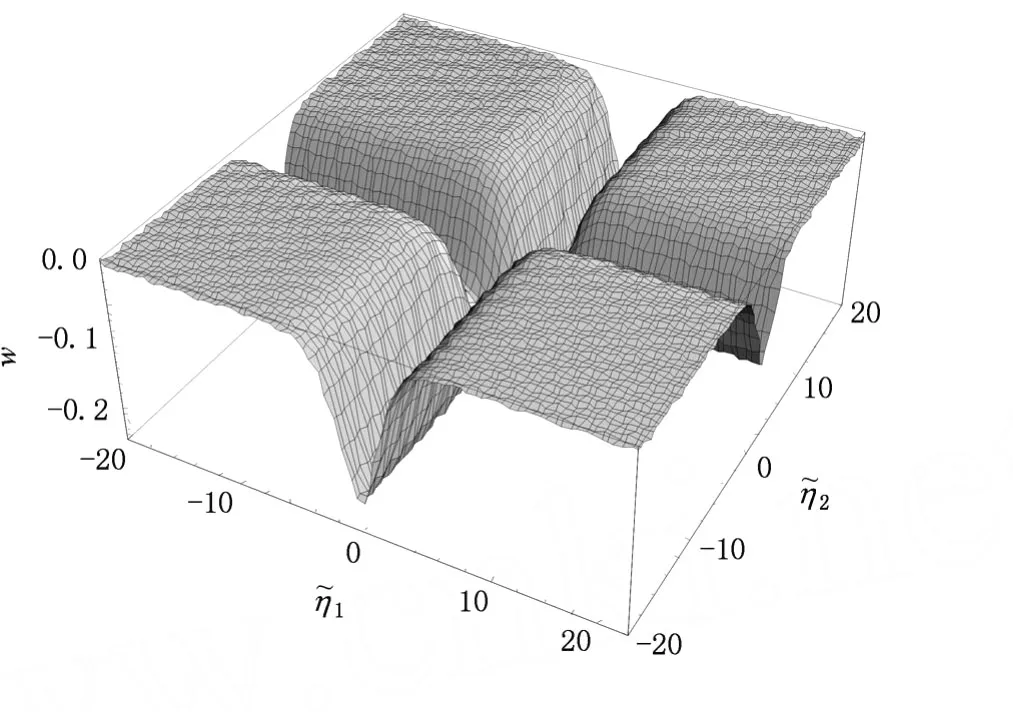
圖2 用Mathematica繪出的(53)式的圖像

3.結論

本文使用的方法具有某種普遍性,利用它不僅可以得到(3+1)維孤子方程的周期解,而且也可以得到其他非線性發展方程的周期解.在極限情況下,它們可以退化為孤子解.

[1]Cao C W,Wu Y T,Geng X G1999J.Math.Phys.40 3948

[2]Cao C W,Geng X G,Wu Y T 1999J.Phys.A 32 8059

[3]Wu YQ 2006Chin.Phys.Lett.23 2629

[4]Wang ML 1995Phys.Lett.A 199 169

[5]Lei Y1999Phys.Lett.A 260 55

[6]Fan E G,Zhang H Q 1998Acta Phys.Sin.47 353(in Chinese) [范恩貴、張鴻慶1998物理學報47 353]

[7]Fan E G 2000Acta Phys.Sin.49 1409(in Chinese)[范恩貴2000物理學報49 1409]

[8]Parkes EJ,Duffy B R 1997Phys.Lett.A 229 217

[9]Fan E G2000Phys.Lett.A 277 212

[10]Zhang G X,Li Z B,Duan Y S 2000Sci.ChianA 30 1103(in Chinese)[張桂戌、李志斌、段一士2000中國科學A 30 1103]

[11]Shi Y R,LüK P,Duan W S,Zhao J B 2001Acta Phys.Sin.50 2074(in Chinese)[石玉仁、呂克璞、段文山、趙金寶2001物理學報50 2074]

[12]Shi YR,LüKP,Duan W S Hong X R,ZhaoJ B 2003Acta Phys. Sin.52 267(in Chinese)[石玉仁、呂克璞、段文山、洪學仁、趙金保2003物理學報52 267]

[13]Guo G P,ZhangJ F 2002Acta Phys.Sin.51 1159(in Chinese) [郭冠平、張解放2002物理學報51 1159]

[14]Liu S K,Fu Z T,Liu S D,Zhao Q 2001Acta Phys.Sin.50 2068 (in Chinese)[劉式適、傅遵濤、劉式達、趙 強2001物理學報50 2068]

[15]Matsuno Y1984Bilinear Transformation Method(Academic Press, Inc.)

[16]Hirota R 2004The Direct Method in Soliton Theory(Cambridge University Press)

[17]Hirota R 1971Phys.Rev.Lett.27 1192

[18]Nakamura A 1979J.Phys.Soc.Jpn.47 1701

[19]Nakamura A 1980J.Phys.Soc.Jpn.48 1365

[20]Fan E G,Hon YC 2008Phys.Rev.E 78 036607

[21]Geng X G2003J.Phys.A 36 2289

[22]Geng X G,Ma YL 2007Phys.Lett.A 369 285

[23]Wu J P 2008Chin.Phys.Lett.25 4192

[24]Farkas H M,Kra I 1992Riemann Surfaces(Springer-Verlag)

PACC:0340K,0290

The periodic wave solution for a(3+1)-dimensional soliton equation＊

Wu Y ong-Qi?

(Mathematics and Computational Science School,Zhanjiang Normal University,Zhanjiang 524048,China)

6 March 2009;revised manuscript

14 April 2009)

A new periodic wave solution for a(3+1)-dimensional soliton equation is found by using the Hirota method and Riemann theat function,from which the soliton solution can be obtained in an appropriate limiting procedure.In addition,the special three-dimensional surface graph of this equation is simulated with the help of Mathematica.

Hirota method,Riemann theta function,(3+1)-dimensional soliton equation,periodic solution

＊湛江師范學院科研基金(批準號:L0803)資助的課題.

?E-mail:yqwuedu@sina.com

＊Project supported by the Science Research Foundation of Zhanjiang Normal University(Grant No.L0803).

?E-mail:yqwuedu@sina.com