一種即開型電子彩票發行方案

孫佳男

西北師范大學數學與信息科學學院 甘肅 730070

0 引言

隨著彩票制作技術的發展，彩票的種類也逐漸多樣化，傳統的彩票有雙色球、3D等，為了適應現代人快節奏的生活，國家彩票發行機構又推出即開型彩票，也叫即開即兌型彩票，就是購票者在一個銷售點上一次完成購票和兌獎全過程的一種彩票。當購票者買到彩票后，刮開兌獎區，馬上就可以知道是否中獎，如果所中獎金在一定范圍內則立即可以在銷售點領取獎金。同時彩票發行機構設獎靈活，可根據不同地區需求，設置適應當地經濟條件的獎金等級，其防偽性能好，安全可靠。

1 新的即開型電子彩票方案

1.1 符號說明

（1）U代表國家彩票發行機構，Z代表指定的彩票銷售方，P代表彩票購買者，ID代表購買者身份。

（2）wnum代表中獎號碼，bon代表獎金金額。

（3）CP代表即開型電子彩票，C Pi代表第i張彩票，代表第i張彩票內容，N代表彩票發行期號，T代表彩票銷售時間。

（4）SC代表簽密算法，DSC代表解簽密算法，PK、SK為彩票購買者公鑰和私鑰。

1.2 新方案的具體流程

我們根據現行的彩票發行方式提出新的發行過程如下：

（1）U：設置wnum和對應bon ，生成CP,U →Z :CP‖wnum，但不發送bon。

（2）Z：收到CP‖wnum后，公布wnum，銷售CP。

（3）P：查看wnum，選擇CP，如果決定購買iCP，則用ID綁定iCP,等待開獎。Z →U：iCP‖ID，U進行保存。

（4）U：T結束后，公布打開CP的方法以及wnum對應的bon。

（5）P：在Z處打開iCP，如果結果與wnum相同，則在Z處兌獎。

（6）當P在Z處兌獎后（只有極少數大獎P在U處兌獎），Z統計已為P兌獎獎金總額sum，Z→U:sum信息；U返還sum給Z。

（7）Z：打開CP，驗證中獎率、返獎率，P如果懷疑公布的wnum和bon，可進行驗證。

1.3 該方案的算法描述

（1）U和Z的初始設置

U的初始設置：U選擇一個隨機數 xA∈，計算 yA←(mod p)，U的公鑰是(p,q,g,,H，E)，私鑰是；其中參數(p,q,g,H,E)和上述Zheng簽密方案系統參數相同。

Z的初始設置：Z選擇一個隨機數 xB∈，計算←(mod p)，Z的公鑰為私鑰為

（2）U生成wnum信息

① 生成wnum 。假設U決定設置n個wnum 。

U：選擇n個隨機數 x1,x2,...,xn∈U（算法Ⅰ），計算←(mod p),(mod p),．．．，←(mod p)。生成n個wnum{y1,y2,...,yn}，并設置每一個wnum對應的bon{ m1,m2,...,mn}。

算法Ⅰ如下：

設特定條件為新產生的隨機數與已產生的隨機數相比如果距離小于特定值，則放棄，重新選取。我們把特定條件抽象為布爾代數F[j]∈{0,1}，F[j]=1表示滿足條件。

Step1 生成數組A，i=1

Step2 產生隨機數j∈[1,q-1]Step3 如果F[j]=1，轉step5 Step4 轉setp2

Step5 A[i]=j,并將 i+1

Step6 如果i<=n 轉step2

否則，數組A中A[1],A[2],...,A[n]為n個滿足條件的隨機數。

如果U要生成下一期彩票wnum，只需要在該算法特定條件中附加不等于往期所有的已選取隨機數，wnum就不可能與往期重復。

② 生成wnum信息。U：再選擇n個隨機數(R1,R2,．．．,Rn)作為P以后驗證時用的參數，計算 yi,mi,Ri的 Hash函數值,i∈[1,n],M1 =h(y1,m1,R1)，M2=h(y2,m2,R2),...，Mn=h(yn,mn,Rn)，然后把 yi與對應Mi組成一對，最后生成wnum信息{（ y1‖M1）‖（ y2‖M2）‖...‖(yn‖Mn)}。

（3）U生成彩票組

① 生成彩票內容 C P*。假設U決定該期彩票組中包含K張CP 。U :選取上述n個有獎隨機數 x1,x2,...,xn（每個中獎號碼對應的離散對數值），還必須選取其它不同于x1,x2,...,xn的隨機數 K1個， K = n + K1。

選取這 K1個數算法是在 n個有獎隨機數已產生前提下繼續執行算法Ⅰ，只是條件附加了不等于已選取的n個隨機數。最后數組A中A[1],A[2],…,A[K]元素即為K張彩票具體內容,i∈[1,K]。

Step1 m=K

Step2 產生隨機數 j∈[1,m]，t=j；

Step3 如果 F[j]=1.轉 step6；

Step4 j=j mod m +1；

Step5 如果j<>t，轉step3；

Step6 將A[j]與A[m]互換，并將m-1；

Step7 如果m>1，轉step2；

最后數組A中存放的是隨機排序后的（ x1,x2,...,xn, ...,xK），即A[i] =,i∈[1,K]。

（4）U發送CP給指定Z

U： MCP←N‖CP‖wnum信息,MCP即為要發送的彩票明文。

U：如果發送 MCP給 Z，則查詢 Z的公鑰，U →Z :SC( MCP),SC采用Zheng簽密方案中簽密算法。

（5）Z銷售CP

Z： MCP←DSC(SC( MCP))，DSC采用 Zheng解簽密算法，其過程用到Z的私鑰 xB和U的公鑰（p,q,g,yA,H,E），解密并驗證通過后，確定 MCP為U發送的有效消息。然后公布wnum信息。

P：如果在未售出CP中選擇購買彩票 C Pi，則在Z處生成已售出彩票即← EPK( C Pi‖ID)，E是U公布的一種公鑰加密算法,Z在已售出彩票列表中增加記錄i，

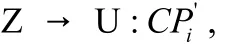
（6）U公布開獎信息以及P兌獎

① T結束后，Z發送未售出彩票序號列表給U ，U :與Z結賬，然后公布 wnum{y1,y2,...,yn}對應的隨機數{R1,R2,...,Rn}和獎金{ m1,m2,...,mn}以及秘密種子 S0和偽隨機數產生算法。

② P：在Z處 C Pi← DSK(，然后利用算法產生偽隨機序列，得到對應的子密鑰 SK，←(C Pi)，得到即 xi。然后計算 gxi(mod p)（其中g和p是U公開的公鑰），如果結果與wnum中 yi相同，則對應bon為 mi。

Z：核對ID后給P兌獎，并保存 xi。

P：如果 mi超過一定范圍，則在U處 C Pi← DSK(，U核實ID后，給P兌獎。

（7）Z領取返還金￥

假設第N期CP中Z實際為n個中獎者兌獎。

Z：統計已兌獎的中獎號碼 yi對應的中獎彩票內容 xi，組成返還金信息 MF{N‖ x1‖ x2‖...‖ xn}，Z → U: MF。

U： （其中 mi為中獎號碼 gxi(mod p)對應獎金），U返還￥。

（8）Z驗證中獎率和返獎率

2 安全性以及性能分析

2.1 安全性分析

（1）彩票銷售的指定性。彩票發行機構用銷售方的公鑰對電子彩票組進行了簽密，只有指定的銷售方用自己的私鑰才能解密并驗證。

（2）彩票內容不可猜測性和保密性。為了保證簽密算法的安全性，參數q必須是一個大素數，一般要求q≈1602 ,而彩票內容是從[1,q-1]之間隨機選取的大整數，而且每個隨機數之間有一定距離，所以對于P和Z是不可能猜到的，同時利用產生的偽隨機序列加密每一張電子彩票，并對其進行了隨機排序，所以加強了對電子彩票內容的保密性。

（3）購買彩票的隨機性。因為彩票銷售時中獎號碼對應的獎金不公開，同時發行機構也可以適當設置沒有獎金的“中獎號碼”，所以防止了購票者對于包含獎金數額大或者中獎號碼多的彩票組全部包買的情況發生。

（4）計算中獎彩票內容的困難性。困難性是基于離散對數問題，即已知iy解不出ix(iy←ixg(mod p))，所以銷售方和購票者不可能知道中獎號碼iy所對應的中獎彩票內容ix。

（5）中獎號碼以及獎金的不可偽造性。銷售方不可能偽造中獎號碼iy，發行機構也不能改變預定的獎金im。基于

（6）電子彩票的私有性。只有購票者用自己的私鑰才能解密已售出彩票，其他人不可能冒領該彩票，如果中獎，銷售方在核實其身份后才兌現其所中獎金。

（7）返還金的真實性。銷售方不可能憑借虛假的返還金信息獲得返還金。

（8）中獎率和返獎率的驗證性。銷售方可以解密每一張彩票，驗證電子彩票的中獎率和返獎率。

2.2 性能分析

（1）Zheng的簽密方案的優點。考慮到彩票發行機構與銷售方通信帶寬方面的限制，該方案簽密算法采用了 Zheng的簽密方案SCS1，該算法在計算以及通信帶寬方面都非常有效，因為消息的對稱加密不會引起數據的擴展，所以簽密密文可以只用2|q|比特再加上被簽密消息的比特數進行發送。

（2）符合特定條件的隨機排序優化算法優點。該算法應用了交換機制，每次交換時，把隨機數組分為A[m+1]到A[K]已排序部分和 A[1]到 A[m]未排序部分，在未排序部分動態產生均勻分布的隨機數。同時該算法采用自環機制(step4)，如果隨機數j不滿足條件，則從起點j開始尋找第一個滿足條件的數，以上兩種機制提高了該算法的計算效率節省了內存。而方案中彩票隨機排序采用該算法，提高了彩票的生成效率。

（3）中獎號碼與銷售數量的無關性。中獎號碼提前設置，其隨機性與彩票銷售數量沒有關系，即開即兌，大幅度縮短了開獎時間。

（4）購票者開獎的簡便性。由于電子彩票發送過程采用Zheng的簽密方案，利用該簽密方案參數下求解離散對數問題的困難性設置中獎號碼與彩票內容，簡化了購票者的開獎步驟，減少了發行方和銷售方的參數設置。

（5）購票者兌獎的實時性。該方案通過設置銷售方領取返還金環節，實現了彩票的即兌性，銷售方只需要發送真實的中獎彩票內容給發行方就可以領取到返還金，方便，快捷，可靠。

3 結束語

本文在即開型彩票例如刮刮樂等在國內發行比較熱的背景下，提出了一種簡單的，容易實現的即開型電子彩票的發行方案。其特點是基于現行的彩票發行模式實現了即開型彩票整個發行過程的無紙化，與傳統的方式即把中獎號碼作為中獎彩票內容相比，該方案采用中獎號碼對應的離散對數作為彩票內容是一個改進，實現了中獎者立即兌獎，也方便了銷售方領取返還金。

[1]鄭東,張彤,陳克非等.基于比特承諾的電子彩票方案[J].電子學報.2000.

[2]鄭東,陳克非,尤晉元.電子彩票“離線”方案[J].通信學報.2001.

[3]孫蕭寒.安全電子彩票方案研究[D].西安電子科技大學.2008.