兩類特殊圖的泛寬度染色

劉秀麗

（菏澤學院數學系，山東 菏澤 274015）

兩類特殊圖的泛寬度染色

劉秀麗

（菏澤學院數學系，山東 菏澤 274015）

研究了圖染色問題中與頻道分配有關的泛寬度染色.給出了兩類特殊圖的泛寬度色數.

泛寬度染色；d-寬度箱；泛寬度色數；雙圖

0 引 言

圖論發展到現在已有許多分支，著色理論是其中之一，且有著極其重要的地位.它起源于150年前的四色猜想.染色問題在組合分析和實際生活中有著廣泛的應用，是圖論研究中一個很活躍的課題，近年來，又提出了許多新的染色問題在頻道分配中的應用，如Bresar等人[1]提出了一種染色-泛寬度染色.在一個給定的網絡中，使用相同廣播頻率的兩個站點的信號將會相互干擾，除非它們的位置相當遠.信號傳播的距離與這些信號的功率直接相關.圖的泛寬度染色是依據頂點之間的距離對頂點的一種剖分.對于不具有特定圖結構的任意圖來說，確定圖中任意兩個頂點的距離是非常困難的，而且在目前已知的結論中，也都是針對具有具體圖結構的圖類來研究的.如在文獻［1］中作者給出了無限正方形和完全圖Kn的剖分圖s（Kn）的泛寬度色數.Scoper[2]研究了樹的泛寬度染色，證明了無限3-正則圖樹的泛寬度色數是7.張珊珊等人[3]研究了輪、扇及完全圖Kn的推廣的hajos sum泛寬度染色，并在另一文獻[4]中研究了圈及其相關圖的泛寬度染色.在文獻［1］中作者猜想：確定任意圖的泛寬度色數問題是NP（有非確定性多項式算法）完備問題.本文研究了兩類雙圖的泛寬度色數.

文中未加說明的記號和術語參見Bondy等人文獻[5-6].

1 預備知識

我們用V（G）和E（G）分別表示圖G的頂點集和邊集.設G是一個簡單圖，對于任意兩個頂點x，y，它們的距離d（x，y）是x-y路長的最小值，特別地，如果沒有x-y路，則 d（x， y）＝ ∞.

定義1[1]設G=（V（G），E（G）），d是一個正整數，X是V（G）的一個子集，如果X中任意兩個點的距離都大于d，稱X是一個d-寬度箱，d叫做X的寬度，顯然，d-寬度箱也是（d-1）-寬度箱、 （d-2）-寬度箱等等.

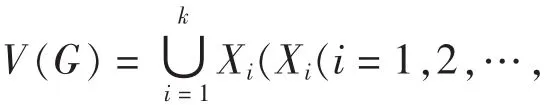
顯然，此處我們的目的是最小化k，可以假設對每個整數i，Xi是一個i-寬度箱.

定義 3 設 G 和 G′均為簡單連通圖， V（G） ={v1，v2，…，vn}， V（G′） ={u1，u2，…，un}.在 G 和 G′之間加匹配 viui（i=1，2，…，n）， 得到新圖 D（G）， 我們稱 D（G）為 G 的雙圖.于是：

2 主要結果及證明

定理 1 設 Pn， P′n為兩條長為 n-1 的路， 其頂點集分別為 V（Pn） ={v1，v2，…，vn}和V（P′n） ={u1，u2，…，un}， 則當 n>5 時， 有 χρ（D（Pn）） ＝ 5.

證明 首先證明 χρ（D（Pn）） ≥ 5.

反證法，假設有一個映射 f： V（D（Pn）） → {1，2，3，4}.對于 D（Pn）上的各個頂點，除了v1u1，v2u2，…，vnun之外都是對稱的，不妨令f（u2）＝1.因為：

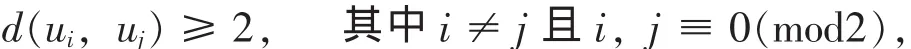
所以可以用 1 來染 uj（j≡ 0（mod2））， 即當 j≡ 0（mod2）時， f（uj） ＝ 1； 又因為：

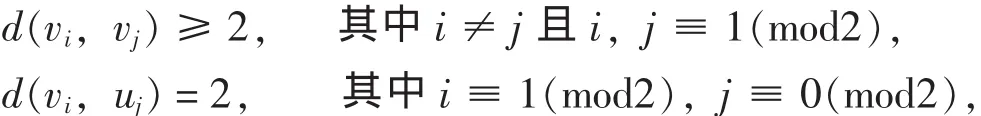
所以可以用 1 來染 vi（i≡ 1（mod2））， 即當 i≡ 1（mod2）時， f（vi） ＝ 1.

對于剩余的未染色的頂點，不妨令f（v2）＝2.因為：

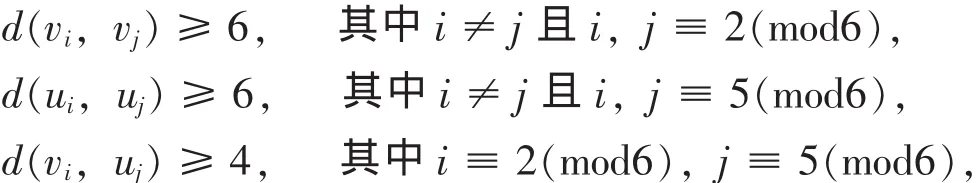
所以可以用 2 來染 vi，uj（i≡ 2（mod6）， j≡ 5（mod6））， 即當 i≡ 2（mod6），j≡ 5（mod6）時， f（vi） ＝ 2， f（uj） ＝ 2.

類似可以用 3 來染 vi，uj（i≡ 4（mod6）， j≡ 1（mod6））， 即當 i≡ 4（mod6）， j≡1（mod6）時， f（vi） ＝ 3，f（uj） ＝ 3.

此時還剩余形如 vi（i≡ 0（mod6））和 uj（j≡ 3（mod6））的點未染，但是 d（v6，u3） ＝ 4，不能用4同時染v6和u3，所以還需要用另一種新的顏色.

類似可以證明其他的染色方式也不行.所以，χρ（D（Pn））≥ 5.

再證 χρ（D（Pn）） ≤ 5.

下面構造一個映射 f： V（D（Pn）） → {1，2，3，4，5}.

當 i≡ 1（mod2）時， 令 f（vi）＝ 1； 當 i≡ 0（mod6）時， 令 f（vi） ＝ 5；

當 i≡ 2（mod6）時， 令 f（vi） ＝ 2； 當 i≡ 4（mod6）時， 令 f（vi） ＝ 3；

當 j≡ 0（mod2）時， 令 f（uj） ＝ 1； 當 j≡ 1（mod6）時， 令 f（uj） ＝ 3；

當 j≡ 3（mod6）時， 令 f（uj） ＝ 4； 當 j≡ 5（mod6）時， 令 f（uj） ＝ 2.

易證映射 f是 D（Pn）的一個泛寬度染色， 所以 χρ（D（Pn）） ≤ 5.

綜上， 當 n>5 時， 有 χρ（D（Pn）） =5.

注 1 特別地， 當 n=3， 4， 5 時， χρ（D（Pn）） ＝ 4.

定理 2 設 Wn， W′n為兩個輪， 其頂點集分別為 V（Wn） ={v0，v1，v2，…，vn}和 V（W′n） ={u0，u1，u2，…，un}， 則 χρ（D（Wn））＝ n+2.

證明 首先證明 χρ（D（Wn）） ≥ n+2.

由圖D（Wn）的結構易知，圖D（Wn）中最長的是 P4，即圖D（Wn）中任意兩點之間的距離都小于等于3，那么最多只有顏色1和2可以染多個頂點，其余的顏色只能用來染一個頂點.相互之間距離大于等于2的頂點構成D（Wn）的獨立集，易知，圖D（Wn）的最多獨立集I滿足滿足任意兩點相互之間的距離大于等于3的頂點集中只有兩個頂點，因此需要顏色數大于等于2n+2-n-2+2=n+2，即χρ（D（Wn））≥ n+2.

再證 χρ（D（Wn））≤ n+2， 即用 n+2種顏色可以完成對圖 D（Wn）的泛寬度染色.

用1來染最大獨立集I中的頂點，用2來染剩余未染的并且滿足距離大于等于3的頂點，對于剩余的2n+2-n-2=n個頂點，因為相互之間的距離都小于等于3，所以n個頂點可以用n種染色來染，染完D（Wn）的所有頂點一共用了n+1+1=n+2種顏色.所以， χρ（D（Wn）） ≤ n+2.

綜上， 有 χρ（D（Wn）） ＝ n+2.

注2 圖的泛寬度染色是依據頂點之間的距離對頂點的一種剖分.對于不具有特定圖結構的任意圖來說，確定圖中任意兩個頂點的距離是非常困難的，而且目前已知的結論中，也都是針對具有具體圖結構的圖類來研究的，并且在文獻［1］中作者也猜想：確定任意圖的泛寬度色數問題是NP完備問題.

下面構造一個算法來實現對任意圖的泛寬度染色.

思想 在第i步從那些未染色的點中，找一個極大的i-寬度箱Xi，把Xi中所有的頂點染顏色i，指標i從1開始，每一步增加1，用k表示i的最終值.

算法

從這個算法可以很容易得出，對于任意圖G，有χρ（G）≤k.在第一步中，當i=1時，V中極大的1-寬度箱就是圖G的最大獨立子集I，即X1=I，由此可以得到：

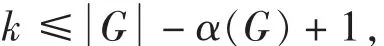
對于很稠密的圖來說，上述式子可以取到等號，即：

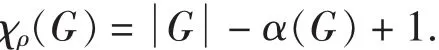
例如完全圖Kn.

3 結 語

本文研究了由兩條路以及兩個圈構成的雙圖的泛寬度染色，并得出了這兩類雙圖的泛寬度色數.本文的不足之處在于研究的圖類簡單，只給出了在兩條路或兩個圈之間加一重匹配.可考慮加多重匹配，還可進一步考慮研究其他圖類的泛寬度色數.

[1]Bresar B,Klavzar S,Rall D F.On the packing number of cartesian products， hexagonal lattice，and trees[J]. Discrete Applied Mathematics， 2007， 155（17）： 2 303-2 311.

[2]Scoper C.An eccentric coloring of trees[J].Australasia J Combin， 2004（29）： 309-321.

[3]張姍姍，劉曉曉，陳麗華.幾類特殊圖的泛寬度色數[J].山東科學，2008，21（04）：32-37.

[4]陳麗華，張姍姍，劉曉曉.圈及其相關圖的泛寬度染色[J].山東科學，2008，21（05）：75-78.

[5]Bondy J A， Murtyu S R.Graph theory with applications[M].London： Macmillan Press， 1976， 75-128.

[6]Bollobas B.Modern graph theory[M].New York： Springer-Verlag， 1998， 145-177.

Abstract：The packing coloring， to be related to frequency assignment problem of coloring problem，were deliberated.The packing numbers of two kinds of graphs were given.

Key words：packing coloring； d-packing； packing chromatic number； double graph

On the Packing Coloring of Two Kinds of Graphs

LIU Xiu-li

（Department of Mathematics， Heze University， Heze 274015， Shandong， China）

O 157.5

A

1001-4217（2010）04-0008-04

2009-09-30

劉秀麗（1977－），女，山東曹縣人，講師，碩士研究生.研究方向：圖論與組合優化.E-mail：liuxiuli1004@163.com