基于相關系數法的數控機床評價模型

楊明川 王春秀

（寧夏大學機械工程學院，寧夏銀川 750021）

基于相關系數法的數控機床評價模型

楊明川 王春秀

（寧夏大學機械工程學院，寧夏銀川 750021）

針對數控機床故障間隔時間分布模型的參數精度不高且不方便計算的問題，基于相關系數法利用Matlab編程來估計數控機床威布爾分布的三個參數，使其既符合精度要求，又易于實現。

數控機床 相關系數法 三參數威布爾分布 Matlab

現在數控機床可靠性的要求越來越高，在可靠性評價之前，需要建立數控機床的可靠性模型。常用的可靠性模型有威布爾分布模型和指數分布模型。指數分布模型認為機床在某一時刻的可靠度與之前的運行時間無關。威布爾分布由“最弱環節模型”推導而出。“最弱環節模型”認為系統、設備等產品的故障起因于其構成元件中最弱元件的故障，這相當于構成鏈條的各環節中最弱的鏈節壽命決定了整個鏈條的壽命。由此可見威布爾分布模型比指數分布模型更加符合實際情況。本文以5臺某系列數控機床半年的26個定時截尾故障數據為例給出具體計算過程。

1 數控機床故障間隔時間的壽命分布模型

根據某數控機床廠提供的數控機床故障間隔時間的歷史記錄來擬合其概率密度函數。本文共采集了5臺國產數控車床的現場故障信息，其具體數據如下表1所示。

表1 某數控機床故障間隔數據

將故障間隔時間的觀測值 t∈［91.94，929.42］分為6組，其組間距為139.67，如表2所示。

表2 故障時間和頻率

以上面六組數據的組中值為橫坐標，故障的頻率為縱坐標，繪制故障間隔時間散點圖［3］，如圖1。

由圖1可知，故障概率密度曲線呈單調下降趨勢，故障間隔時間分布不會是正態分布或對數正態分布，而有可能是指數分布或者威布爾分布。

2 威布爾分布參數估計

三參數威布爾分布包含形狀參數m，位置參數γ和尺度參數t0。由于位置參數不容易估計，所以傳統方法將威布爾分布的三分布參數轉換為兩分布參數，僅對形狀參數和尺度參數估計［1］。固然給計算帶來了一定的方便，但是由于其沒有考慮位置參數的特性，決定了計算值與實際值之間會出現較大的誤差。而采用極大似然估計法可以求解三個參數并且有較高的精度，但是需要解三個超越方程并且其計算過于麻煩。針對這一問題，本文采用相關系數法，先計算其位置參數再計算形狀參數和尺度參數［2］。進而得出三參數威布爾分布模型，這可以提高數控機床可靠性分析與評價的精確性。

2.1 相關系數法估計的理論

當威布爾分布的形狀參數等于1時，便轉化為指數分布。即威布爾分布包含了指數分布［3］，因此可以認為故障概率密度函數服從威布爾分布。為了得到準確的模型，本文先估計其位置參數。

三參數威布爾分布的累積失效概率函數計算公式［4］如下所示

式（1）中：m 為形狀參數，m ＞0；γ 為位置參數，γ ＞0；t0為尺度參數，t0＞0；t為產品壽命，t≤γ；F（t）為累積失效概率分布函數，0≤F（t）≤l

對式（l）進行等價變形處理，可得下式

式（3）所表示的是等分度平面坐標系x－y中的一條斜率為m，截距為B的直線方程即回歸直線。對于三參數威布爾分布，當位置參數γ已知時，就可以利用回歸分析通過最小二乘法求出其m和t0的估計值；若位置參數γ未知則需要先求出γ的值再估計m和t0的值。本文就基于這種情況進行分析。由式（3）可知，當γ估計正確時，X與Y存在線性關系。將其在威布爾概率紙上描點表現為各點近似分布在一條直線上，可以通過最小二乘法求解m和t0；反之則X與Y之間就不存在這種線性關系。當^γ逐漸增加時，相關系數R逐漸增加；當^γ達其理論值γ時，R也達到它的最大值［5］，此時x與Y成線性關系；當^γ進一步增大時，R又逐漸減小。由此可見，只要求出相關系數R最大時的^γ，就是位置參數的最佳估計值。

2.2 用相關系數法估計其位置參數的方法

從上述可知，求位置參數γ的最佳估計值的過程就是求相關系數R最大值的過程。根據高等數學求極大值的方法，只需求出相關系數R對γ的一階導數，并令其等于零，然后解方程即可。此時求出的^γ就是R最大時的位置參數的最佳估計值^γ［6］。

對于容量為n且服從威布爾分布的數控機床故障間隔時間，將其數據觀測值按從小到大的順序依次排列，對應的樣本分布函數用F（ti）表示，則有

對于威布爾分布恒有R＞0，故求R對γ的一階導數與求R2對γ的一階導數對求γ而言是等價的。為簡化算式，這里計算R2對γ的一階導數。按照高等數學求導公式對其求導并進行化簡得

于是求解γ的方程已經給出。式（4）所包含的僅有一個未知量，γ完全可以求出。與極大似然法求解三個復雜的方程，并且進行迭代相比減少了大量的運算。

3 相關系數法估計在威布爾分布中的應用

3.1 編制M文件

首先根據二分法［7］編制M文件保存在Matlab的默認路徑當中，以便以后調用。下面是程序代碼：

3.2 編制主函數文件

分別計算其方程中的各個值如下所示。

3.3 計算位置參數

有根區間的左右限是根據其位置參數的圖估法計算［3］得出來的。

用bisection（f，0，100，20，10^（－3））計算其參數得出結果為69.98。

3.4 計算其形狀參數和尺度參數

由于其計算出來的γ＞0，所以對其三參數威布爾分布進行的變換為t′=t－γ，由此可將其變換為二參數威布爾分布。其數據在直角坐標系中符合直線分布，變換后的數據可根據最小二乘法原理進行計算。用Matlab編寫的具體程序如下：其中t為觀測數據，t1為變換后數據

4 威布爾的擬合度檢驗

對于數控機床故障概率密度函數的分布要進行擬合優度檢驗，這里選用K－S檢驗（柯爾莫哥洛夫－斯米爾諾夫檢驗）法［3］。將n個（這里是26個）故障時間數據按由小到大的次序排列，根據假設的分布，計算每個數據ti對應的故障概率函數F（ti）。將其與經驗分布函數Fn（ti）進行比較，其中差值的最大絕對值即檢驗統計量Dn的觀察值。將Dn與臨界值Dan進行比較，滿足下列條件，則接受原假設，否則拒絕原假設。

原假設 H0：參數的值服從 m=1.316 1，γ =69.98，η=292.94的三參數威布爾分布。

列表計算理論分布和經驗分布的差異度，如表3所示。

這樣Dn＜，原假設成立，既數控機床的參數值符合 m=1.316 1，γ =69.98，t0=1 764.12 的三參數威布爾分布。

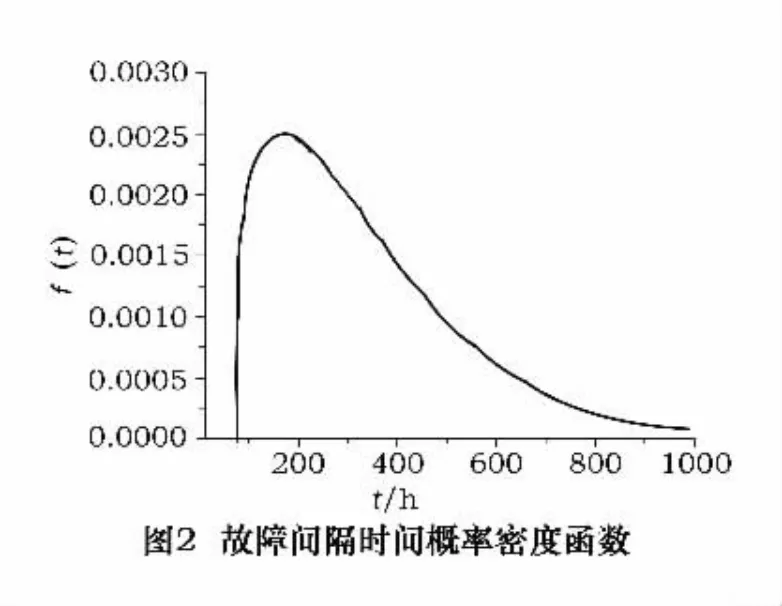
5 故障間隔時間概率密度函數與分布函數的確定

數控機床的故障間隔時間概率密度函數為

數控機床的分布函數為

f（t）和F（t）的曲線分別如圖2和圖3所示。

表3 數控機床的K-S檢驗計算

布爾分布用上述計算方法得出形狀參數為1.923 4，尺度參數為92 116，數控機床的故障間隔時間概率密度函數為

6 壽命分布模型的分析

從圖3可以看出，數控機床在早期故障率高發期運行時間過長，在偶然故障階段運行時間過短，這是國產數控機床可靠性不高的重要原因。因此提高可靠度應縮短早期故障期，并盡量延長偶然故障階段。

早期故障出現在產品開始工作的初期，在此階段，故障率高，可靠性低，但隨工作時間的增加而迅速下降。數控機床發生早期故障的原因主要是由于設計、制造工藝上的缺陷，或者是由于零件和材料的結構缺陷所致。因此要縮短此故障期就應該在出廠前進行相應的試驗，盡可能的減少早期故障次數，根據其位置參數可以合理制定早期故障排除試驗時間。

偶然故障期是數控機床的正常工作期，其特點是故障率比早期故障率小得多，近似為一常數。這個時期的故障是由偶然不確定因素所引起的，故障發生的時間也是隨機的，所以不同的廠家會有不同的原因，要提高其可靠度就應該到使用方進行詳細調研，根據其反饋進行具體的分析。

7 結語

（1）采用三參數威布爾分布模型進行分析更加符合實際工作環境，可以得出更精確的數控機床可靠性的各個參數，為數控機床可靠性的提高和可靠性的增長奠定分析基礎。

（2）結合其工程實際和精度要求，給出了估計數控機床三參數威布爾分布的方法。

（3）為提高數控機床可靠性，減少其早期故障時間提供理論支持。

1 張英芝，申桂香，吳甦等.隨機截尾數控機床三參數威布爾分布模型.吉林大學學報，2009（3）

2 嚴曉東，馬翔，鄭榮躍等.三參數威布爾分布參數估計方法比較.寧波大學學報，2005（9）

3 賀國芳.可靠性數據的收集與分析.北京：國防工業出版社，1995（12）

4 劉惟信.機械可靠性設計.北京：清華大學出版社，1995（2）

5 方志強，高連華.三參數威布爾分布在壽命分析中的參數估計.裝甲兵工程學院學報，1999（3）

6 胡恩平，羅興柏，劉國慶.三參數Weibull分布幾種常用的參數估計方法.沈陽工業學院學報，2000（9）

7 姜健飛.數值分析及其Matlab試驗.北京：科學出版社，2004（6）

如果您想發表對本文的看法，請將文章編號填入讀者意見調查表中的相應位置。

Evaluation Model on NC Machine Based on Correlation Cofficient Method

YANG Mingchuan，WANG Chunxiu
（School of Mechanical Engineering，Ningxia University，Yinchuan 750021，CHN）

The parameter of NC machine MTBF method is not precise and convenient calculate.This document estimates three parameter of Weibull distribution based on the correlation cofficient using the Matlab.It causes both easy to achieve ，and to meet the accuracy requirement.

NC Machine；Correlation Cofficient Method；3 －Parameter Weibull Distribution；Matlab

楊明川，男，1984年生，碩士研究生，主要研究方向為先進制造技術。

（編輯 周富榮） （收修改稿日期：2009－08－10）

10119