Ne 原子與H2分子碰撞的同位素替代效應研究*

令狐榮鋒徐梅王曉璐呂兵楊向東?

1)(四川大學原子與分子物理研究所，成都610065)

2)(貴州師范大學物理與電子科學學院，貴陽550001)

(2009年6月30日收到;2009年7月30日收到修改稿)

Ne 原子與H2分子碰撞的同位素替代效應研究*

令狐榮鋒1)2)徐梅1)王曉璐1)2)呂兵1)2)楊向東1)?

1)(四川大學原子與分子物理研究所，成都610065)

2)(貴州師范大學物理與電子科學學院，貴陽550001)

(2009年6月30日收到;2009年7月30日收到修改稿)

使用密耦近似(Close-Coupling)方法、采用Tang-Toennies勢模型計算了惰性氣體原子Ne與H2分子及同位素D2分子在碰撞能量為83.8 meV時的微分散射截面及分波截面，并與實驗值和文獻值進行比較.計算得到的微分散射截面值與實驗值符合得較好，分波截面值與文獻值也相符合.使用同樣的方法和模型，文中對Ne-H2(D2，T2)三個體系的微分截面和分波截面進行了系統計算和比較分析，得出對稱同位素替代碰撞體系的散射截面規律.

Ne-H2(D2，T2)碰撞，Tang-Toennies勢模型，密耦方法，同位素替代

PACC:3440，3450

1. 引言

原子與分子碰撞實驗及理論研究是原子分子物理十分重要的研究方向，原子分子碰撞在很多物理過程中扮演著重要角色，如氣體激光、共振熒光過程、等離子體物理、氣相弛豫過程、氣相反應和輸運性質、大氣物理、星際空間云團的冷卻過程等等［1］.碰撞作用機理及計算方法的研究成果為以上各領域實驗現象的解釋、可觀測量的預言提供了大量的參考信息.隨著交叉分子束實驗技術的發展，碰撞散射實驗成為獲得原子分子間相互作用勢信息的理想途徑，碰撞過程的計算研究是測試、驗證假設勢能模型的有效方法.

通過對有關原子與分子間振動和轉動激發及非彈性碰撞研究文獻的檢索表明，人們對惰性氣體原子與H2分子之間的相互作用及碰撞十分關注［2—14］，這是因為通過對原子與H2分子及其同位素分子碰撞的研究，可以了解它們的振動和轉動激發截面及其隨能量變化的規律，可以得到一些從實驗中難以得到的數據.對于He-H2碰撞系統，已有較多研究，其中Tadeusz［15］用從頭算勢能面計算了He-H2系統的振轉去激發截面，結果與實驗符合較好;Tang和Teonnies［16］在理論和實驗上對He-H2的相互作用勢及散射截面進行了深入的研究;John等［17］用準經典軌道方法對He-H2碰撞系統的分子能量轉移進行了計算，對碰撞振動弛豫和高溫離解過程進行了討論等.我們曾用Tang-Toennies(T-T)勢模型和密耦近似方法［18—20］計算了He同位素與H2，D2，T2，及He與鹵化氫分子等體系，取得了一些成果，計算結果與文獻和實驗相符.

對于Ne-H2碰撞系統，實驗研究和理論計算的報道都較少，Faubel等［21］通過分子束實驗研究了Ne-H2體系的彈性和非彈性微分截面，并從理論上研究了分波截面.最近Lique［22］用從頭算得到了Ne-H2的相互作用勢數據，并計算了該體系的微分截面.本文采用T-T勢模型通過密耦近似(closecoupling)方法，計算了惰性氣體原子Ne與H2，D2分子碰撞能量為E=83.8 meV時的微分散射截面及分波截面，并與Faubel和Lique的結果進行比較，本文計算的微分散射截面值與實驗值符合得較好，分波截面值與文獻值也相符合，說明本文采用的勢模型和截面計算方法是可行的.因此，本文使用同樣的方法，對Ne-H2，Ne-D2，Ne-T2三個體系的微分截面和分波截面進行了系統計算和比較分析，得出了Ne與H2分子對稱同位素替代碰撞體系的散射截面規律.

2. 體系的相互作用勢

對于H2分子的勢能函數，本文采用Murrell-Sorbie函數擬合.Murrell-Sorbie函數已被公認為較準確的雙原子分子的勢能函數.本文通過與實驗值比較，選擇QCISD/6-311++G(3df，3pd)對H2分子進行單點能掃描，對應于不同核間距的勢能值擬合為如下形式的標準勢能函數Murrell-Sorbie(M-S)勢函數［23］: V=－De(1+a1ρ+a2ρ2+a3ρ3)exp(－a1ρ)，(1)其中ρ=R－Re，R為核間距，Re為平衡核間距，De，a1，a2，a3為擬合參數，H2分子的勢阱參數與實驗值的比較和M-S函數擬合參數列入表1中.

對于原子與雙原子分子相互作用勢，人們在長期的研究中，在分子勢能函數的基本模型的基礎上，提出了許多原子與雙原子分子相互作用的勢模型，但Ne原子與H2分子間的相互作用解析勢不多見.T-T勢［16］充分考慮了自洽場短程勢、長程吸引色散勢和其他效應(如交換色散、高階項等)，較準確地反映了真實體系的相互作用，是一種比較好的勢模型.T-T勢模型計算的阱參數與實驗值十分符合.該模型如下:

表1 H2分子的勢阱參數與實驗值的比較和M-S函數擬合參數

其中，V0(R)為球對稱勢，V2(R)P2(cosθ)為各向異性勢，θ為R與分子鍵軸的夾角，而V0(R)和V2(R)又可表示為:

式中V11(R)=V(R，0°)，V⊥(R)=V(R，90°)，而V11，V⊥由三部分組成

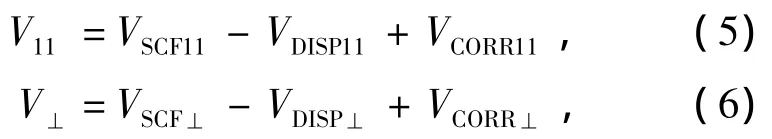
其中VSCF(R)為短程自洽場排斥勢，VDISP(R)為長程Van de Waals色散吸引勢，VCORR(R)是交換色散修正勢，可分別表示如下:

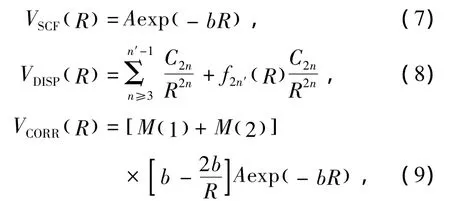
其中，A，b是Bohn-Mayer勢參數，f2n′(R)是色散勢的衰減函數，n′是VDISP(R)收斂后的最大n加1，即n′=n+1，C2n是色散系數，M(i)是交換色散勢勢參數.

Tang和Toennies通過理論計算并與實驗值比較得到Ne與H2的相互作用的色散參數C6，C8，C10，Γ6，Γ8和Γ10.本文使用Hariharan計算的短程自洽場排斥勢數據，擬合了A‖，A⊥，b⊥和b‖值，該模型相互作用的參數見表2.

表2 Ne-H2相互作用的色散參數

將表2參數代入以上模型中，計算得出Ne-H2體系的勢阱位置和深度，計算值和實驗值符合得很好，說明T-T勢模型準確表達了體系的原子與分子相互作用勢.表3列出了Ne與H2相互作用的勢參數與實驗值的比較.

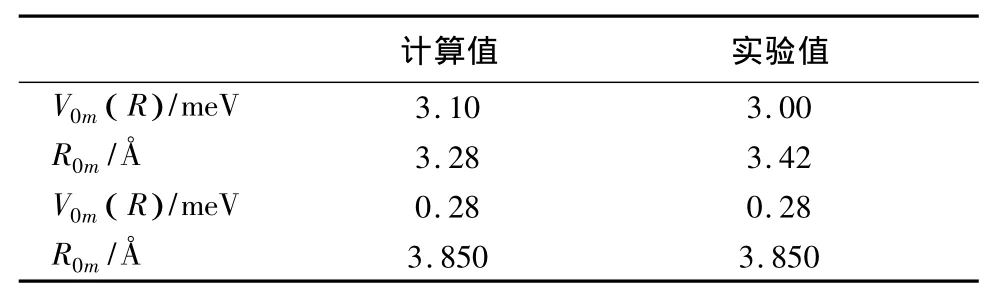
表3 Ne-H2相互作用的勢參數與實驗值的比較

根據Bohn-Oppenhemer近似，同位素的替代不改變體系的相互作用勢能面的形狀，因此，對Ne-D2，Ne-T2兩體系，本文采用了與Ne-H2體系相同的勢能面.

3. 密耦近似方法

根據Bohn-Oppenheimer近似，原子A和雙原子分子BC碰撞體系的總波函數ψ(+)α(R，r)滿足的Schrdinger方程為:

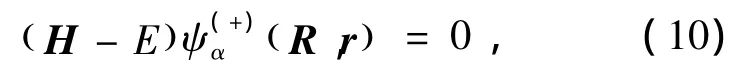
式中r是雙原子分子中兩核之間的相對位置矢量，R是入射原子A相對靶分子BC質心的相對位置矢量，如圖1所示.E是體系的總能量，(+)表示波函數滿足外向邊界條件，α表示入射通道量子數的完全集.體系的Hamilton算符為:

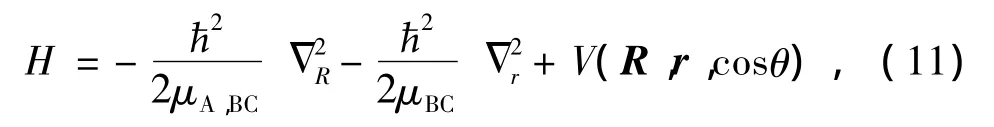
其中μA，BC和μBC分別為總體系和雙原子分子的約化質量，cosθ=^R·r^.

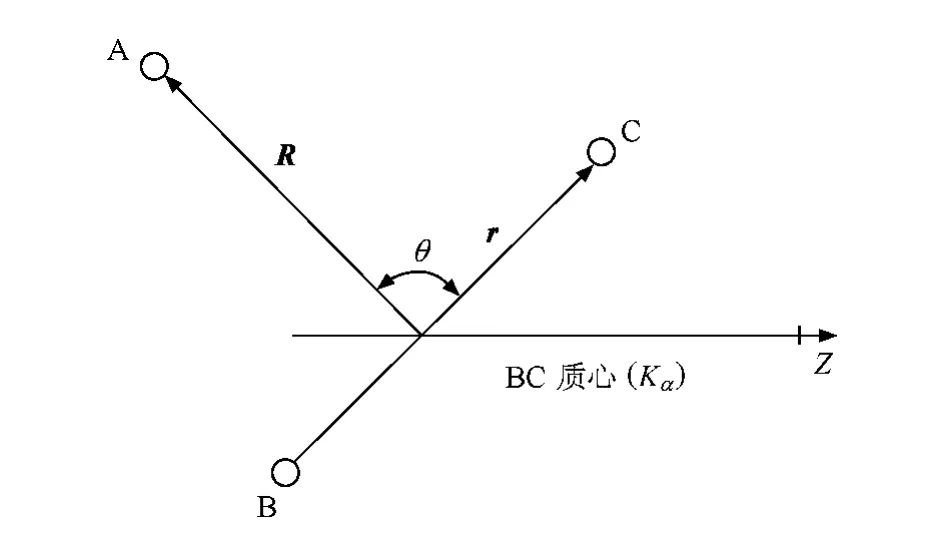
圖1 原子與雙原子分子碰撞的幾何圖形

如圖1所示，從(nαJα)到(nβJβ)的微分散射截面由下面公式給出［1］:

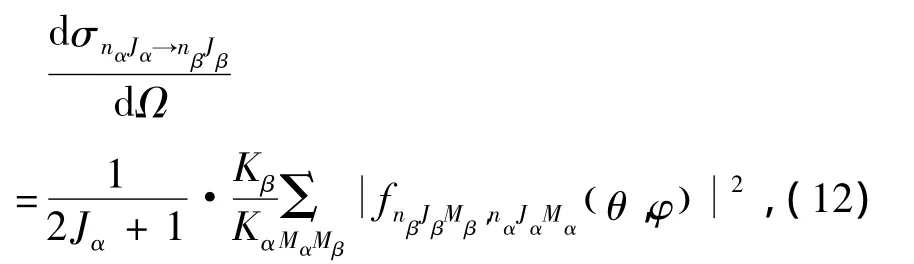
式中

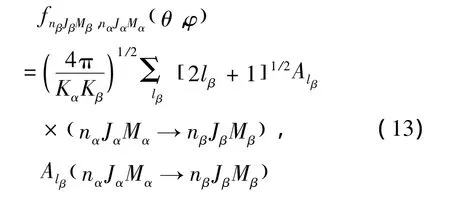
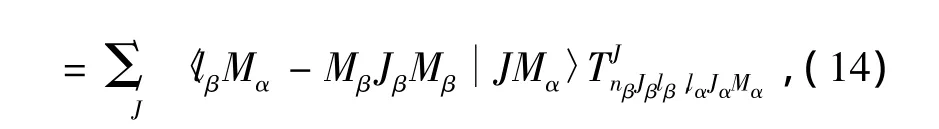
從(nαJα)躍遷到(nβJβ)的振轉激發的分波散射總截面為

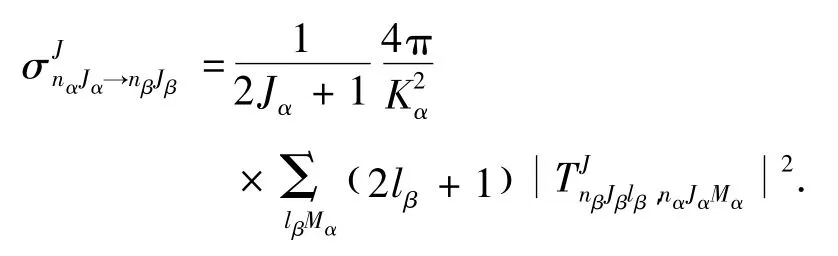
4. Ne-H2(D2，T2)碰撞體系的散射截面

采用上述勢模型和近似方法，本文對碰撞能量為E=83.8 meV時Ne-H2，Ne-D2，Ne-T2體系的微分截面和分波截面進行了計算和比較分析，得出了H2分子對稱同位素替代碰撞體系的散射截面的規律.

4.1. 微分截面

圖2是本文計算的Ne-H2體系在碰撞能量為E =83.8 meV時微分截面值的角分布與實驗值和文獻值的比較圖.小方框是Faubel等［21］的實驗值，實線為本文計算值，虛線為Lique［22］的計算值.從圖中可看出:在彈性碰撞00-00時，本文計算的微分散射截面值與實驗值符合得很好，與文獻值也相符合;對于非彈性碰撞00-02，本文計算值與實驗值有一定的誤差，在小角度部分與Lique的計算結果相比與實驗值更為接近，說明本文采用的勢模型和截面的計算方法是較為可靠和準確的.

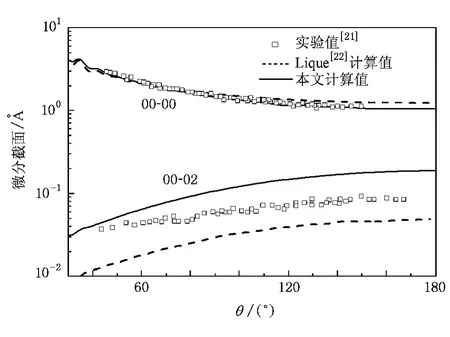
圖2 碰撞能量為E=83.8 meV時Ne-H2彈性00-00和非彈性00-02碰撞微分截面與實驗值和文獻值的比較

因此本文用同樣的勢模型和截面的計算方法，計算了碰撞能量為E=83.8 meV時Ne-D2，Ne-T2等氫同位素體系的微分截面，如圖3和圖4所示.圖3是三個體系的00-00躍遷的微分截面隨散射角變化的角分布曲線.

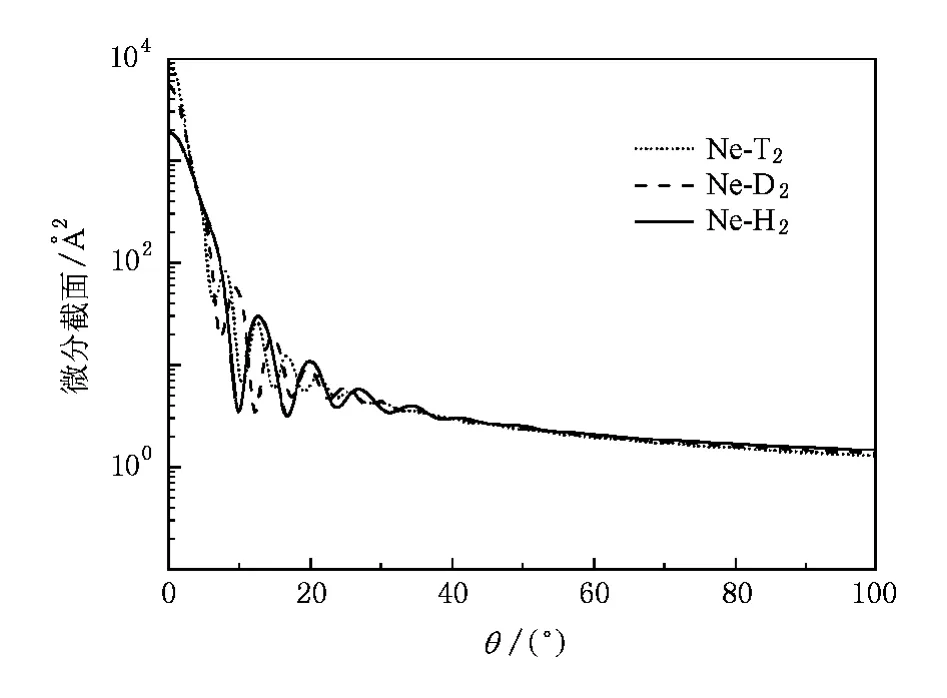
圖3 碰撞能量為E=83.8 meV時Ne-H2，Ne-D2，Ne-T2體系的彈性00-00微分截面隨散射角的變化規律

圖4 碰撞能量為E=83.8 meV時Ne-H2，Ne-D2，Ne-T2體系的非彈性00-02微分截面隨散射角的變化規律

從圖中可以看出，在散射角很小時(0°—3°)，三個體系的微分截面差別很大，較重體系Ne-T2的微分截面值最大，較輕體系Ne-H2的微分截面最小，在散射角3°—6°，三個體系的微分截面值相差不大，而在6°—35°各體系微分截面迅速振蕩減小，但較重體系Ne-T2的截面值趨于平緩所需的角度值則較小，而較輕體系截面值趨于平緩所需的角度值則較大.在35°—60°區間，各體系微分截面值基本趨于相同，在60°—180°區間，可以看出三個體系微分截面值的差別也很小，較重體系的截面值略小于較輕體系的截面值，這表明了三個同位素靶分子對氖原子碰撞微分截面的散射規律.

從圖3中還可以看出，Ne-H2，Ne-D2，Ne-T2三個體系各級振蕩間隔分別為Δθ=7°，5°，4°，遵從以下規律:Δθ～，其中μ是體系的約化質量，E是碰撞能量，可以看出在相同的能量碰撞時，隨著體系約化質量增大，體系的振蕩間隔減小.三體系的第一個振蕩極小值出現位置也有差別，Ne-H2在10°，而Ne-D2與Ne-T2體系的第一振蕩極小值分別出現在7°和6°的位置，這個現象同樣可以用對應的衍射角分布規律得到解釋:由de Broglie長公式λ= h/(μ是體系的約化質量，E是入射能量)和衍射公式2dsinθ=nλ，在相同入射原子能量下，對于不同體系，則有sinθ∝n/，μ越大，同一級衍射極小值位置越小.

圖4是碰撞能量為E=83.8 meV時三個體系的00-02躍遷的微分截面隨散射角的分布曲線.從圖中可以看出，三個體系非彈性散射振蕩主要發生在小角區，在散射角為0°—30°區間，三個體系的微分截面都是振蕩增加，較重Ne-T2的體系振蕩幅度大，之后三個體系的微分截面值單調增加，而且較重體系的截面值比較輕體系的截面值大.

4.2. 分波截面

圖5是Ne-D2體系碰撞能量為E=83.8 meV時本文計算的彈性分波截面和Faubel等［21］的計算值的比較曲線，從圖中可看出兩曲線的振蕩規律和趨勢基本符合，所需的收斂分波數一致.本文使用同樣的勢模型和截面的計算方法，計算了Ne-H2，Ne-D2，Ne-T2體系的彈性分波截面和非彈性分波截面，如圖6和圖7所示.

圖5 碰撞能量為E=83.8 meV時Ne-D2體系本文計算的彈性分波截面和Faubel等的計算值的比較曲線

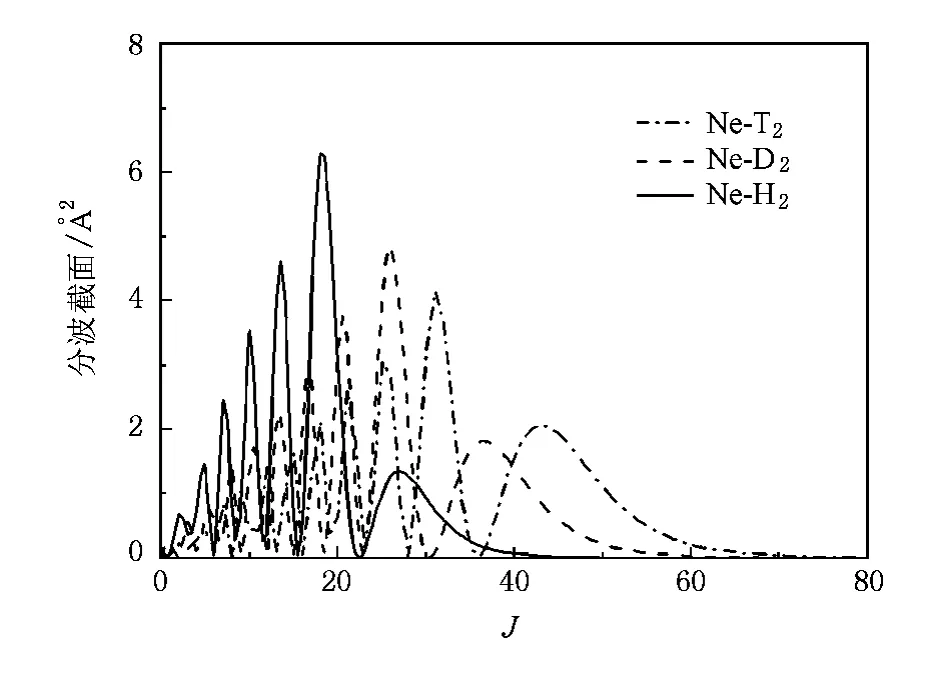
圖6 Ne-H2，Ne-D2，Ne-T2體系在碰撞能量為E=83.8 meV時彈性00-00分波截面隨總角動量量子數J的變化曲線

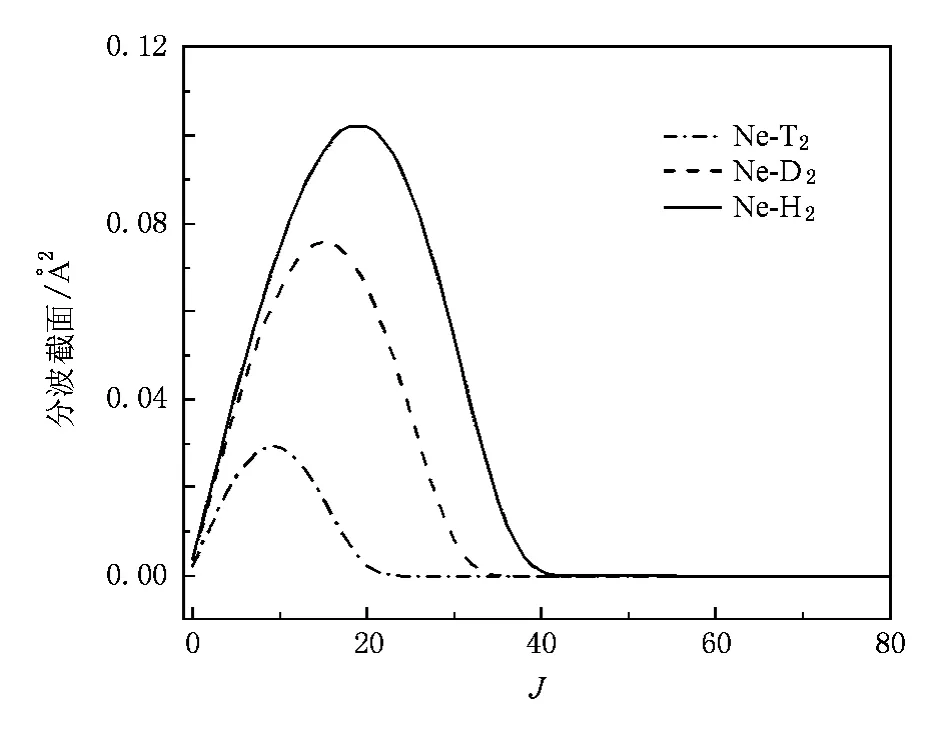
圖7 Ne-H2，Ne-D2，Ne-T2體系在碰撞能量為E=83.8 meV時的非彈性00-02分波截面隨總角動量量子數J的變化曲線

圖6是這三個體系在相同碰撞能量為E=83.8 meV彈性分波截面隨總角動量量子數J的變化曲線，從圖中可以看出:三個碰撞體系的彈性分波截面隨J的變化曲線的形狀相似，分波截面隨J的增大而不斷振蕩，且振幅越來越大，最后達到一個最大值后，較快地趨近于0，但都出現了明顯的尾部效應.尾部效應表現為分波截面達到最大值后又出現一個較小的極大值，是因為當入射粒子的角動量增大到粒子在經典散射情形下已不可能與散射勢場發生作用時，由于量子效應，粒子仍會受到勢場的散射而產生的.在相同碰撞能量時，體系的約化質量越高，量子效應越明顯.三個體系的散射極大值的位置隨著體系約化質量的增加向大J方向移動，收斂所需的量子數也隨著增加.Ne-H2體系需要J=42個分波收斂，而Ne-D2，Ne-T2分別需要J= 59，J=72才收斂.其物理實質可如下解釋:用半經典公式L≤ka表示對中心場中的勢散射，即只有粒子的軌道角動量量子數L不大于入射粒子對應的de Broglie波波數k與中心場有效作用半徑a的乘積時，粒子才能被散射中心場散射;又k=，所以L≤，由于僅考慮分子的轉動激發，即jα=0，因而入射通道的總角動量與軌道角動量相等，即J=Lα，故J≤，即對于同一入射能量和同一散射勢場J∝，得到收斂的截面所需的分波數和體系的約化質量的平方根成正比，所以相同碰撞能量時較重體系的分波截面收斂所需的分波數就多.

圖7是Ne-H2，Ne-D2，Ne-T2三體系的非彈性00-02分波截面隨總角動量量子數J的變化曲線.從圖中可以看出:碰撞體系的彈性和非彈性分波截面隨J的變化曲線的形狀相似，即截面只經過一個極大值便很快趨于零，沒有出現振蕩現象.三體系中，較重體系的截面的極大值反而較小，對應的量子數也較小;而較輕體系的截面的極大值較大，對應的量子數也較大.

5. 結論

1)經過與實驗值和文獻值的比較說明，使用TT勢模型和密耦方法，可以準確地得到Ne與H2分子及其同位素D2，T2分子的碰撞體系的散射截面.

2)對于相同的碰撞能量，Ne與H2分子及其同位素D2，T2分子的彈性和非彈性碰撞微分截面主要發生在小角部分，彈性碰撞時隨著體系約化質量增大，體系的振蕩間隔減小.

在地區分布方面（表 3），優質推文集中在中部地區和東南沿海地區，這與區域經濟發展相關。和行政層級分布同理，經濟發達地區的民主黨派微信公眾號所投入的人力物力資源相對較多，運營經驗也相對豐富。其中發布優質推文最多的公眾號所屬省份是河北省，共發布9篇。

3)相對碰撞能量一定時，隨著體系約化質量的增加，三個同位素體系的彈性分波截面最大值的位置向大J的方向移動，截面值減小，而尾部效應逐漸增強.

4)對于Ne與H2分子及其同位素D2，T2分子的非彈性散射分波截面，其規律都是截面只經過一個極大值便趨于零，其峰值的位置隨著體系的約化質量的增加而向小J的方向移動，但截面值則逐漸減少.

［1］Scole G 1988 Atomic and Molecular Beam Methds(Oxford: Oxford University)p18

［2］Yu C R，Zhang J，Jiang G S 2009 Acta Phys.Sin.58 2376(in Chinese)［余春日、張杰、江貴生2009物理學報58 2376］

［3］Tang K T，Toennies J P 1982 J.Chem.Phys.76 2524

［4］Yang X D 1991 J.Sci.China Ser.A 34 48

［5］Yang X D，Hu D，Jing F Q 1998 J.Phys.B At.Mol.Opt. Phys.31 826

［7］Shi D H，Sun J F，Zhu Z L，Yang X，Liu Y F，Ma H Z 2007 Acta Phys.Sin.56 4435(in Chinese)［施德恒、孫金鋒、朱遵略、楊向東、劉玉芳、馬恒中2007物理學報56 4435］

［8］Yu C R，Feng E Y，Cheng X L，Yang X D 2007 Acta Phys. Sin.56 4441［余春日、鳳爾銀、程新路、楊向東2007物理學報56 4441］

［9］Shen G X，Linghu R F，Wang R K，Yang X D 2007 Chin. Phys.16 3352

［10］Shen G X，Wang R K，Linghu R F，Yang X D 2008 Acta Phys. Sin.57 3452(in Chinese)［沈光先、汪榮凱、令狐榮鋒、楊向東2008物理學報57 3452］

［11］Yu C R，Wang R K，Yang X D，Yin X C 2008 Acta Phys.Sin. 57 2906(in Chinese)［沈光先、汪榮凱、楊向東、尹訓昌2008物理學報57 2906］

［12］Yang C L，Zhu Z H 1999 Acta Phys.Sin.48 1852(in Chinese)［楊傳路、朱正和1999物理學報48 1852］

［13］Choi B H，Tang K T 1976 J.Chem.Phys.65 5528

［14］Bowers M S，Faubel M，Tang K T 1987 J.Chem.Phys.87 5687

［15］Tadeusz O 1981 Chem.Phys.61 405

［16］Tang K T，Toennies J P 1978 J.Chem.Phys.68 5501

［17］John E D，Susanne R，H T 1980 Chem.Phys.50 175

［18］Shen G X，Wang R K，Linghu R F，Yang X D 2008 Acta Phys. Sin.58 3827(in Chinese)［沈光先、汪榮凱、令狐榮鋒、楊向東2008物理學報58 3827］

［19］Yu C R，Wang R K，Cheng X L，Yang X D 2008 Acta Phys. Sin.57 2577(in Chinese)［沈光先、汪榮凱、程新路、楊向東2008物理學報57 2577］

［20］Dai W，Feng H，Sun W G，Tang Y J，Shen L Y，Jiang Z 2008 Acta Phys.Sin.57 0143(in Chinese)［戴偉、馮灝、孫衛國、唐永建、申立于、江周2008物理學報57 0143］

［21］Faubel M，Glanturco F A，Fagnetti F，Rusan L Y，Tappe U，Teonnies J P 1994 J.Chem.Phys.101 8800

［22］Lique F 2009 Chem.Phys.Lett.471 54

［23］Zhu Z H 1996 Atomic and Molecular Reaction Statis(Beijing: Science Press)(in Chinese)［朱正和1996原子分子反應靜力學(北京:科學出版社)］

PACC:3440，3450

*Project supported by the National Natural Science Foundation of China(Grant Nos.10964002，10974139)，the Specialized Research Fund for the Doctoral Program Higher Education of China(Grant No.20050610010)，the Natural Science Foundation of the Education Bureau of Guizhou Province，China(Grant No.2005105)and the Governor's Foundation for Science and Education Elites of Guizhou Province［Grant No. QSZHZ2006(113)］，the Science Technology Foundation of Guizhou Province of China［Grant No.QKHJZ(2009)2066］.

?Corresponding author.E-mail:xdyang@scu.edu.cn

The effect of symmetrical isotopic substitution in Ne-H2collision*

Linghu Rong-Feng1)2)Xu Mei2)Wang Xiao-Lu1)2)Lü Bing1)2)Yang Xiang-Dong1)?
1)(Institute of Atomic and Molecular Physics，Sichuan University，Chengdu610065，China)
2)(School of Science，Guizhou Normal University，Guiyang550001，China)
(Received 30 June 2009;revised manuscript received 30 July 2009)

The differential and partial wave scattering cross sections of Ne-H2(D2，T2)collisions have been calculated by closecoupling approximation method using Tang-Toennies potential model at the incident energy of 83.8 meV.The calculated differential cross sections are in good agreement with the experimental data and the partial wave cross sections match well with the published data.With the same method and potential model，the differential cross sections and the partial wave cross sections of Ne-H2(D2，T2)collisions have been derived and analyzed.The rules of the effect of symmetrical isotopic substitution are obtained.

Ne-H2(D2，T2)collision，Tang-Toennies potential model，close-coupling method，symmetrical isotopic substitution

book=89,ebook=89

*國家自然科學基金(批準號:10964002，10974139)、高等學校博士學科點專項科研基金(批準號:20050610010)、貴州省教育廳自然科學重點項目(批準號:2005105)、貴州省優秀科技教育人才省長基金(批準號:QSZHZ2006(113))和貴州省科學技術基金(批準號:QKHJZ［2009］2066)資助的課題.

?通訊聯系人.E-mail:xdyang@scu.edu.cn