Banach不動點定理的推廣及應用
張 超
(淮南師范學院數學與計算科學系,安徽 淮南 232001)
Banach不動點定理的推廣及應用
張 超
(淮南師范學院數學與計算科學系,安徽 淮南 232001)
本文主要討論完備距離空間中Banach不動點定理,給出了定理的一些推廣結果和改進形式,并舉例說明了Banach不動點定理在經濟上的應用。
壓縮映射;Banach不動點定理;完備空間;均衡
1 引言
不動點理論[1]是目前正在迅速發展的非線性泛函分析理論的重要組成部分,它與近代數學的許多分支有著緊密的聯系。泛函分析[3,5,6]以其高度的統一性和廣泛的應用性在現代數學領域占有重要的地位。微積分中的隱函數存在唯一性定理,代數方程、微分方程和積分方程的求解都可以歸結為泛函分析中的Banach不動點定理來求某映射的不動點。Banach不動點定理實際上是算子方程的求解問題,它提供了解的逼近程序和近似解的構造。本文就從其數學本質出發,討論完備賦范線性空間 Banach不動點定理,給出了定理的一些推廣結果和改進形式,并舉例說明了Banach不動點定理在經濟上的應用。
定義1.1[1]稱 T:(X,ρ)→(X,ρ)是一個壓縮映射。如果存在0<α<1使得ρ(Tx,Ty)≤α ρ(x,y)(?x,y∈X)。
定義 1.2[4]設 X是線性空間,E?X稱 E為一凸集,如果λx+(1-λ)y∈E(?x,y∈E,?0≤λ≤1)。
定義 1.3[2]給定一個私有制經濟我們說配置和價格向量 P構成一個競爭(或瓦爾拉斯)均衡。如果它們滿足下列條件:
(3)市場出清:對于每一種商品
2 主要結果
定理2.1[1](B anach不動點定理)設 (X,d)是完備距離空間,T∶X→X并且對任意x,y∈X,有 d(Tx,Ty)≤θd(x,y),其中 0<θ<1,則存在唯一的∈X使得
現在我們將定理 2.1進行推廣,有以下定理:
定理 2.2 設(X,d)是完備的,T是X到自身的映射,且存在 n>1使 Tn=TTT……Τ∶X→X是壓縮映射,則 T∶X→X有唯一的不動點 x∈X。
證明:由定理 2.1 有唯一的 x∈X使得 Tnx =x因為 Tn(Tx)=Tn+1x =T(Tnx) =Tx故 Tx也是 Tn的唯一不動點,所以 x =Tx即 x是 T的不動點。若 y =Ty顯然y也是 Tn的不動點,由 Tn的不動點的唯一性,知必有 x=y即 T的不動點是唯一的,證畢。
例 設 F∶R→R且 F(x)在R上可導,并且滿足 |F′(x)|≤α<1,則由中值定理 |F(x) -F(y)|=|F′(ξ)(x-y)|≤α|x-y|(ξ在 x與 y之間)即 d(F(x),F(y))≤αd(x,y)。0≤α<1,故 F是壓縮映射,R完備,從而方程 F(x)=x。必有唯一的實數根 x任取 x0∈R由迭代法:xn=F(xn-1)。n=1,2,……,可得近似解 xn的誤差估計
下面我們將巴拿赫不動點定理中的壓縮因子α的條件放寬,可得下面定理。
定理 2.3 設(x,d)是完備距離空間,F是X→X的映射,不必連續,但滿足以下條件:對任意 ε>0總存在δ>0使得當 d(x,Fx)<δ時 F[B(x,ε)]?B(x,ε)這里B(x,ε)表示以x為中心以 ε為半徑的實心球,那么當對某 u∈x有 d(Fnu,Fn-1u)→0時。序列{Fnu}收斂于F的不動點。
證明:記 u的 n次迭代 Fnu為 un先證{un}是柯西列。給定 ε>0取N充分大,使當 n≥N時 d(un,un+1)<δ(ε)因 d(un,Fun)<δ按條件成立。F[B(un,ε)]?B(uN,ε)因此 FuN=uN+1∈B(uN,ε)用數學歸納法可證對一切 k≥0,Fkun=un+k∈B(un,ε)即 d(un,un+k)<ε對k≥0都成立,這表明{un}是柯西列。
由于 X是完備的,存在 u使 un→u,可證 u是 F的不動點,如若不然,則 d(u,Fu)= α >0我們取使得。仍由條件可知將有另一方面,有。可知這個矛盾說明證畢。
定理 2.4 設(X,d)是完備的距離空間,若 d(Fx,Fy)≤α(x,y)d(x,y)。其中 a∶X×X→R+是二元函數,具有性質:對任何閉區間[a,b](a>0),滿足 sup({α(x,y)}/α)≤d(x,y)≤b=λ(a,b)<1則 F有唯一的不動點 u,且 n次迭代值 Fnx→u對任何 x∈X都成立。
證明:對任何 x∈X序列{d(Fnx,Fn+1x)}是不增的,故必收斂于某常數 a≥0。今證 a=0,對充分大的 n,d(Fnx,Fn+1)≤a+1。對這種 n及 c=λ(α,α+1),用歸納法將可得α≤d(Fn+kx,Fn+k+1x)≤ckd(Fnx,Fn+1x)≤ck(α+1),因 0 因此 F[B(x,ε)]?B(x,ε),即 F有唯一的不動點,證畢。 命題 3.1 假設 z(p)是定義在 p∈Rn ++上的函數,滿足 (1)z(p)是連續的;(2)z(p)是零次齊次的;(3)z(p)P;(4)存在一個 s>0使得 zl(p)≥-s;(5)如果 pm→p,這里 p≠0,存在某個五條性質。那么方程組 z(p)=0一定有解。因此,對于任意的純交換經濟,如果0每個消費者 i的偏好≥,i是連續的、嚴格凸的和強單調的,那么一定存在一個瓦爾拉斯均衡。 我們記 f(p)?△里的元素為 p。 (1)對于任意的我們構造一個不動點對應,對于任意的 p∈△0,我們定義 f(p)=即是給定現行價格 p所有使得超需求向量的值最大的q∈△組成它的一個對應,這個對應f()的經濟含義是它相當于一個規則。按照這個規則,現行價格向刪除超需求的方向調整,實際上就是把具有最大超需求的商品的價格調整到最高的價格上去。或者我們有 因此,如果 z(p)≠0那么 f(p)??△ =△-△0這里 ?△表示 △的邊界點的集合。如果 z(p) =0那么 f(p)=△。 (2)對于任意的 p∈?△我們構造一個不動點對應。對于任意的 p∈?△我們定義 f(p)=注意到如此構造的對應使得 ?△上的點不可能是不動點,因此如果 p∈?△那么 pp>0所以 p f(p)。 (3)f()的一個不動點的一個均衡,假設 p∈f(p)在 (2)里我們已經指出 p ?△所以 p? 0如果 z(p)≠0,由(1)知,f(p)? ?△ =△-△0不可能有 p∈f(p)。因此如果 p∈f(p),一定有 z(p)=0。 (4)不動點對應 f()是凸集。如果 p∈△0對于任意的 q1,q2∈f(p),λ∈[0,1]由 f(p)的定義,對于任意的 q∈△′有 z(p)qi≥z(p)q′,i=1,2,…從而 z(p)[λq1+(1-λ)q2]≥z(p)q′所以λq1+(1-λ)q2∈f(p)。同樣的,如果 p∈?△對于任意的 q1,q2∈f(p)。λ∈[0,1]。由 f(p)的定義,有 pqi=0,i=1,2…從而 p (λq1+(1-λ)q2)=0所以λq1+(1 -λ)q2∈f(p)。為了證明 f()的上半連續性,考略兩個序列 pm→p,qm→q這里 qm∈f(pm)我們需要證明 q∈f(p),分兩種情況證明:p∈△0和 p∈?△。如果 p∈△0,那么對于充分大的m,有 pm? 0由于任意的 q′∈△有 z(pm)qm≥z(pm)q′由 z()的連續性,我們有z(p)q≥z(p)q′所以 q∈f(p)如果 p∈?△,假設 pt>0我們將證明對于充分大的m,有。從而 ql=0因此 q∈f(p),由于 pl>0,存在一個 ε>0使得對于充分大的m有 pml> ε,如果 pm∈?△由 f(pm)的定義,有=0。如果 pm∈△0命題 3.1的題中條件 (4)和(5)蘊涵,對于充分大的m。我們必定有因此=0為證明上述不等式,注意到由命題 3.1中條件(5),此不等式的右邊趨于無窮大,如果左邊是負的,上述不等式顯然成立,如果它是正的,那么上述不等式仍然成立,這里 s由命題 3.1中條件(4)給出。 (5)由不動點定理告訴我們任意一個從非空凸緊集到自身的凸值,上半連續對應有一個不動點,由于 △是非空凸緊集,f()是一個凸值,上半連續對應,所以存在一個 p∈△滿足p∈△由 p∈f(p)。由 (3)可得這個 p就是均衡價格向量。 [1]D.R.斯瑪特著,張石生,康世錕,馬意海譯 .不動點定理 [M].重慶:重慶出版社,1982. [2]張定勝編著 .高級微觀經濟 .鄒恒甫總主編 .現代經濟學前沿叢書 [M].武漢:武漢大學出版社,2000. [3]夏道行等編著,實變函數與泛函分析 [M].人民教育出版社,1978. [4]鄭維行,王聲望編 .實變函數與泛函分析概要 (第二冊)[M].北京:人民教育出版社,1980. [5]Walter Rudin.FunctionalAnalysis[M].北京:機械工業出版社,2004. [6]Ruth F C.FunctionalAnalysis inModernAppliedmathematics[M].London:Academ ic Press,2009. (責任編輯:劉洪基) Generalization and Application of Banach Fixed Point Theorem ZHANG Chao In this paper,the author studies Banach fixed point theorem in complete distance space,and gives some extended results and its improved forms,also illustrates its application to economy. contractive mapping;Banach fixed point theorem;complete space;equilibrium O18 A 1671-7406(2010)03-0022-04 2009-11-23 淮南師范學院青年教師科研資助計劃 (項目編號:2007Lkq06)。 張 超 (1974—),男,安徽固鎮人,碩士,副教授,研究方向:金融數學。3 應用
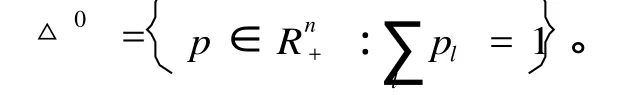
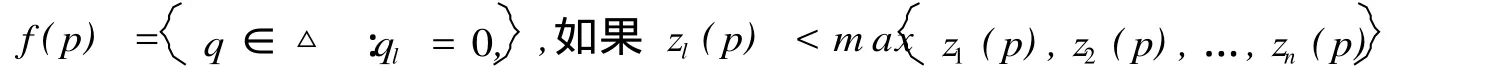
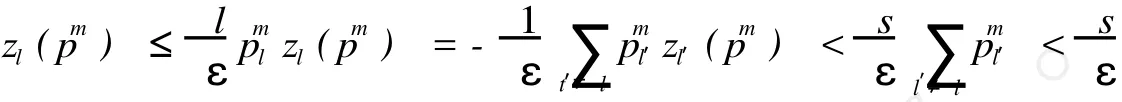
(Departm ent of M athem atics and Computer Science,Huainan N or mal University, Huainan232001,China)

