用高斯定理求電場的條件是滿足環路定理
2010-09-06 07:08:02陳信義
物理與工程 2010年3期
陳信義
(清華大學物理系,北京 100084)
用高斯定理求電場的條件是滿足環路定理
陳信義
(清華大學物理系,北京 100084)
通過舉例說明用高斯定理求電場的條件是:僅由對稱性分析就能得出滿足環路定理的電場形式.
對稱性;高斯定理;環路定理
當電荷分布具有充分的對稱性時,恰當地選取高斯面,就能把高斯定理簡化為只包含一個未知量 E的代數方程,從而可以簡單地求出空間各點的電場.有的同學提問:只有聯合高斯定理和環路定理才能完整地表達靜電場的性質,為什么在這種情況下只用高斯定理就能求出電場?通過對比均勻帶電無限長和有限長細棒兩種情況可以說明,用高斯定理求電場的條件是:僅由對稱性分析就能得出滿足環路定理的電場形式.
對于均勻帶電無限長細棒,由對稱性分析可知其電場是軸對稱分布,并且空間各點場強的方向都沿半徑.在圓柱面坐標系中,場強的形式可以表示為 E=E(ρ)ρ^,此類電場滿足環路定理因此,只用高斯定理就能求出均勻帶電無限長細棒的電場.
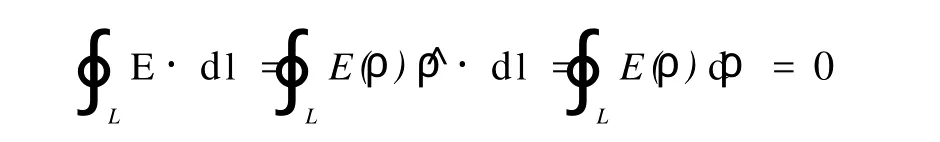
如果帶電細棒為有限長就不行了,這時雖然電場分布仍為軸對稱,但僅由對稱性分析不能確定帶電棒的中垂面之外各點場強的方向,也就無從滿足環路定理.因此,只用高斯定理無法求出有限長帶電棒的中垂面之外各點的電場.
2009-09-28)

