齒輪模數的現場測繪

李紅英

（山西大同大學工學院，山西大同 037003）

齒輪模數的現場測繪

李紅英

（山西大同大學工學院，山西大同 037003）

齒輪模數是齒輪幾何尺寸計算的重要參數.對于損壞齒輪，生產現場要求準確、快速地確定其模數，以便及時配制.經過嚴密計算和實踐驗證，用公法線長度測繪法確定齒輪模數可滿足要求.

齒輪模數 公法線長度 快速測繪 跨齒數 幾何尺寸

齒輪箱是各類機械的變速傳動部件,包含軸、齒輪、滾動軸承和緊固件等.由于制造、裝配誤差或不適當的條件(如載荷、潤滑等)下工作,使箱中齒輪的損壞率高達60%,有齒的斷裂、磨損、齒面疲勞和齒面塑性變形等,這些都會影響齒輪傳動的平穩性和承載能力.因此對齒輪進行測繪,成為重新配制齒輪的重要環節.[1]

齒輪測繪就是用量具對齒輪實物的幾何要素(如齒頂圓直徑da、全齒高h、公法線長度Wk、中心距a、齒數z及螺旋角β等)進行測量,推算出原設計的基本參數(如模數m、壓力角a、齒頂高系數h*a、頂隙系數c*及變位系數x等),并計算出制造時所需的尺寸.在維修工作中,當齒輪損壞嚴重,一些參數無法測得時,需要同時測量與其配對的齒輪及相關零件,根據其嚙合中心距a和齒數z,重新設計齒形,以確定有關參數.

通常,在確定齒輪基本參數前,首先要了解齒輪的生產國別,認定該齒輪所采用的標準制度.其次,由于齒輪的許多參數已標準化,而且是相互關聯的,所以測繪中的計算值應該與其標準值進行比較后,再確定參數值.本篇僅探討齒輪模數的確定法.

1 齒輪標準制度的識別法[2]

(1)中國、日本、法國等多數國家生產的齒輪采用米制,即模數制,以模數m(單位為mm)作為計算齒輪幾何尺寸的依據,齒輪的壓力角a=20°,齒頂高系數h*a=1.0(正常齒制)或h*a=0.8(短齒制);英、美等少數國家生產的齒輪,采用英制,為徑節制,以徑節DP(單位為1/in)作為計算依據,其壓力角a除20°以外,還有14.5°或15°,齒頂高系數h*a=1.0或h*a= 0.875.對英制產品,除航空、航海等特別精密的機器設備,為確保性能和安全可靠,應允許保留英制尺寸和參數外,其余英制尺寸原則上應換算成公制尺寸,同時要求尺寸后面保留小數點后3位數.

模數 m=p/π

徑節 DP=z/d 或 DP=π/p

公英制換算公式：m=25.4/DP mm(1in=25.4mm)

式中,p-周節；z-齒數；d-分度圓直徑.

(2)齒輪標準制度也可通過觀察分辨齒形特征來識別.如圖1所示,齒形彎曲,齒槽根部狹窄且圓弧大,為模數制;齒形平直,齒槽根部較寬且圓弧小,為徑節制；齒形細長的為標準齒,齒形短粗的為短齒.短齒主要用于汽車、坦克、拖拉機、電力機車等.

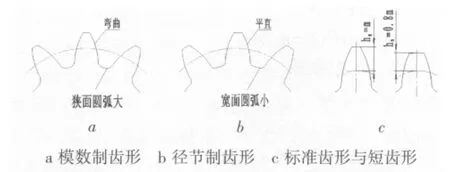
圖1 齒形的識別

2 基本參數——模數的確定

模數是齒輪的一個重要參數,標準直齒圓柱齒輪各部分的幾何尺寸,都是以模數、齒數和壓力角三個基本參數為依據計算得到的.其中,模數是齒輪所有幾何尺寸計算的基礎.對于齒輪而言,齒數是顯而易見的,分度圓壓力角為20°,只有模數需要測繪才能得到.模數的確定方法有多種,但在測繪現場要求準確、快速地確定模數,以便及時對損壞齒輪進行配制.

2.1 齒輪模數的幾何尺寸測繪法

2.1.1 用幾何尺寸測量值確定齒輪模數[3]

(1)用測定的齒頂圓直徑da(或齒根圓直徑df)計算確定模數

1)對于偶數齒齒輪,可用游標卡尺直接測量得到da和df(如圖2a所示);

2)對于奇數齒齒輪,不能直接測量得到,需要測量并計算得出.[2]

方法I:卡尺的一側在齒頂,另一側在齒間,測得值為da′(如圖2b所示),通過幾何關系推算獲得da=kda′,式中k為校正系數,可由“奇數齒齒輪齒頂圓直徑校正系數”表查得到.

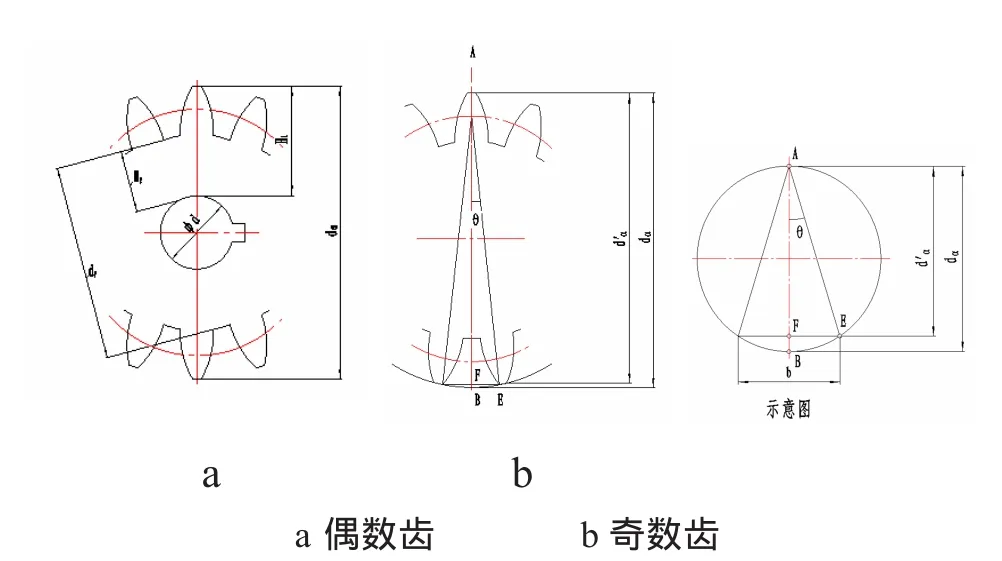
圖2 齒頂圓直徑da的測量

從圖2 b中可看出⊿ABE中

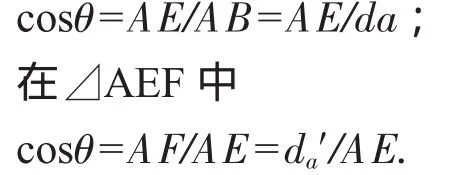
將二式相乘得

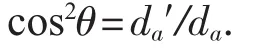
所以,da=da′/cos2θ，

取k=1/cos2θ,則da=kda′.

方法Ⅱ:對于奇數齒中間有孔的齒輪,亦可用間接測量的方法,即測量內孔直徑Φd、內孔壁到齒頂的距離H1或內孔壁到齒根的距離H2(見圖2 a),計算得到：

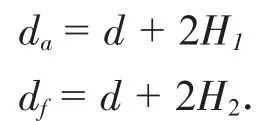
公式推導:[3][4][7]

①標準齒輪(以測繪齒頂圓直徑為例)

齒頂圓直徑 da=d+2ha.

因為,分度圓直徑 d=m z，

齒頂高 ha=ham，

所以,da=m z+2 h*am，

故，模數 m=da/(z+2h*a)，

式中,z已知；da為可測量數值.

同理,斜齒圓柱齒輪法向模數計算公式為:

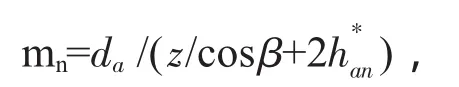
式中,β為螺旋角.

上述模數計算公式中,齒頂高系數h*a和頂隙系數c*以其標準值(正常齒h*a=1.0,c*=0.25;短齒h*a= 0.8,c*=0.3)代入進行計算,所得值m(mn)與表1“漸開線圓柱齒輪模數m”中的標準值相對照,選相符或接近的值.若差值較大,在確定測量值無誤的情況下,考慮為變位齒輪.[2]

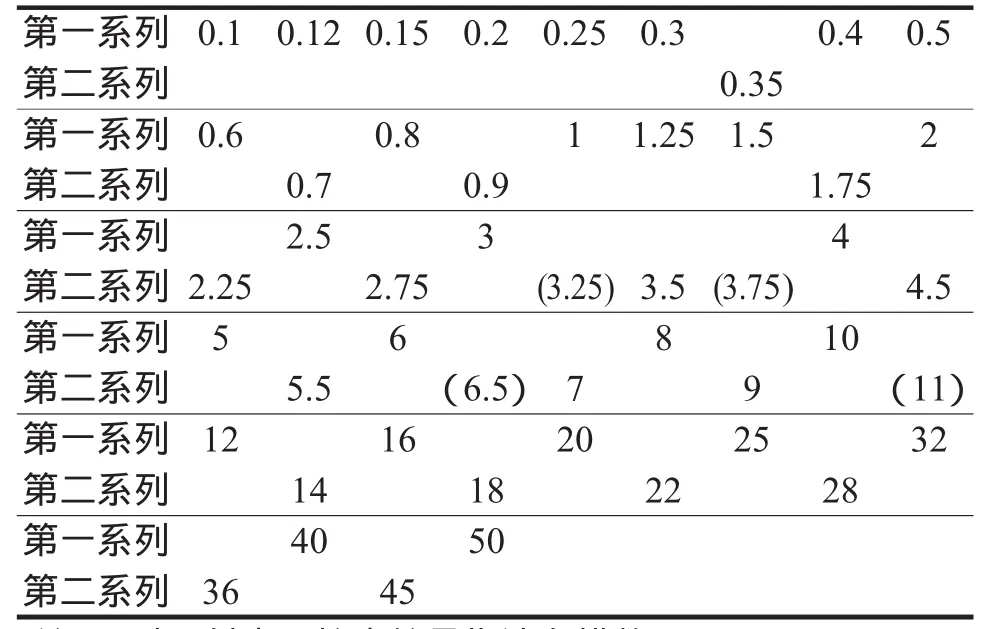
表1 漸開線圓柱齒輪模數m(GB1357—87)(mm)

②變位齒輪 (同標準齒輪相同的原理可得)

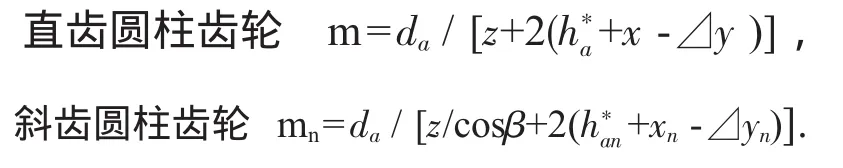
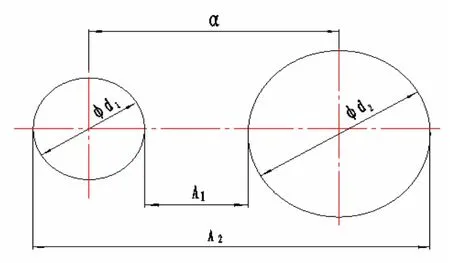
圖3 中心距a的測量

⑵用測定的中心距計算確定模數

中心距a的測量如圖3所示,用游標卡尺測量A1、A2,孔徑Φd1和Φd2,然后按下式計算:

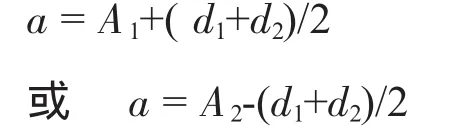
所以,標準齒輪的模數計算公式:

直齒輪 m=2a/(z1+z2)；

斜齒輪 mn=2a cosβ/(z1+z2).

2.1.2 幾何尺寸測繪法確定齒輪模數的缺點

①計算公式復雜,難以記憶,不便于生產現場快速確定齒輪模數.

②若損壞齒輪的齒廓磨損量較大,齒頂圓直徑發生變化,使da的測量值誤差增大,從而使計算的模數值m(或mn)不準確;測量中心距時,由于孔的圓度、錐度及兩孔軸線的平行度對中心距的影響,使測量值不準確 .[2]

③對于變位齒輪,在模數計算公式中還存在未知量——變位系數,(同時存在兩個未知量:變位系數x和模數m),故無法直接確定出模數值.[4]

2.2 齒輪公法線長度的測繪

在實踐中,鑒于幾何尺寸測繪法確定齒輪模數的種種弊端,經過探索、計算和反復驗證,在生產現場可用公法線長度測繪法準確、快速的確定損壞齒輪的模數.[5]

2.2.1 齒輪模數的公法線長度測繪法

公法線長度Wk可用游標卡尺或公法線千分尺測量(如圖4所示).測量時,盡可能使卡尺的量腳平面切于分度圓附近,避免卡尺接觸齒尖或齒根,這樣測得的尺寸精確度高.

以測繪直齒圓柱齒輪為例[1][3][5]

圖4 公法線長度的測量

如圖4所示,為標準直齒圓柱齒輪,Wk為跨齒數k的公法線長度、Wk+1為跨齒數k+1的公法線長度,rb為基圓半徑,pb為基圓齒距 (基節),sb為基圓齒厚.

①標準齒輪公法線長度:

Wk=m W′=mcos a［(k-0.5)π+z inv a］，

式中,W′=cos a［(k-0.5)π+z inv a］,（可查表，

W′為m=1mm時標準齒輪的公法線長度)；

k為跨齒數；inv a為漸開線函數(可查表).

Wk+1=m W′k+1=mcos a［(k+1-0.5)π+z inv a］，

所以 Wk+1-Wk=mπcos a，

導出 m=(Wk+1-Wk)/πcos a,

可見,變位齒輪模數的確定與變位系數無關.所以，用公法線長度測繪法確定齒輪模數,其測繪公式為:m(n)≈(Wk+1(n)-Wk(n))/3.此結論對直齒、斜齒圓柱齒輪或變位齒輪都適用.

2.2.2 跨齒數的選擇[6]

測量公法線時,跨齒數太多或太少都會使千分尺量腳靠近輪齒頂部或根部,形成與齒廓分度圓不相切的接觸.為獲得精確的公法線測量值,必須確定好跨齒數.

⑴標準直齒圓柱齒輪的跨齒數計算公式

k=0.5+za/180°，

當a=20°時,k=0.5+z/9.

⑵斜齒圓柱齒輪的跨齒數計算公式

k=0.5+z′an/180°，

當an=20°時,k=0.5+z′/9.

式中,z′是假想齒數,z′=z inv at/inv an

(an=20°時,inv at/inv an值可查表).

⑶變位齒輪的跨齒數計算公式

直齒輪 k=0.5+za/180°+2x cot a/π；

斜齒輪 k=0.5+z′an/180°+2x ncot an/π.

2.2.3 模數的測量步驟

①由k=0.5+z/9計算k值,確定k+1值,此時應注意k、k+1值必須取整數;

②用公法線千分尺測Wk、Wk+1值,考慮到公法線長度的變動誤差,每次測量時,必須在同一位置,即取同一起始位置、同一方向進行測量;[2]

③由公式m(n)≈(Wk+1(n)-Wk(n))/3計算模數;④按標準化系列對模數計算值進行圓整.

3 結論

(1)公法線長度測繪法,克服了廢舊齒輪齒廓磨損對測繪值的影響,提高了測繪值的準確性與模數計算值的精確度.如設齒輪磨損量為δ,[5]

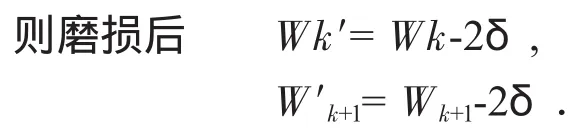
因此，W′k+1-Wk′=(Wk+1-2δ)-(Wk+1-2δ)=Wk+1-Wk，從而消除了磨損誤差.

(2)推導公式m(n)≈(Wk+1(n)-Wk(n))/3,k=0.5+z/9適用于不同類型齒輪模數的確定,故此公式具有計算簡便,易掌握,便于現場測繪.

(3)該方法可對變位齒輪進行測繪.

[1]鄭建中.機器測繪技術[M].北京:機械工業出版社,2001：131－158.

[2]張建中.機械設計基礎[M].徐州:中國礦業大學出版社,2002：99－150.

[3]陳澤艮，忻良昌.公差配合與技術測量[M].北京:機械工業出版社,1986：236－254.

[4]鐘秉林，黃仁.診斷學[M].北京:機械工業出版社,2005：150.

[5]郭攀成.用公法線長度測繪法確定齒輪模數的簡易方法[J].機械研究與應用，2004,17（3）：26－27.

[6]朱理.機械原理[M].北京:高等教育出版社,2004：155－197.

[7]黃錫愷,鄭文偉.機械原理[M].北京：高等教育出版社,1981：153－216.

[8]李曉沛,張琳娜,趙鳳霞.簡明公差標準應用手冊[M].上海：上海科學技術出版社，2005：439－499.

M apping of G ear M odulus on the S cene

LIHong-ying
(School of Engineering，ShanxiDatong University，Datong Shanxi，037003)

The gearmodulus is an gear geometry size calculates important parameter.For the damaged gear,the requirements of produces scene accurately and rapidly determines itsmodulus so that timely fitting of a gear.Pass strictly calculated,and verified repeatedly in practice,use common normal length mappingmethod to determ ine gearmodulusmay satisfy the requirements

gearmodulus；c ommon normal length；fastmapping；cross teeth,geometry

TH132.412

A

〔編輯石白云〕

1674-0874(2010)01-0075-04

2009-08-05

李紅英（1965-），女，山西原平人，實驗師，研究方向：力學、金相分析及公差測量.