一元回歸在射表符合系數曲線制作中的應用

梁文娟，江 波，撒彥成

（1.黃山學院數學系，安徽黃山245041；2.中國華陰兵器試驗中心，陜西華陰 714200）

一元回歸在射表符合系數曲線制作中的應用

梁文娟1，江 波2，撒彥成2

（1.黃山學院數學系，安徽黃山245041；2.中國華陰兵器試驗中心，陜西華陰 714200）

針對現有射表符合系數曲線繪制過程中存在的不足，運用一元回歸方法對其進行改進，并驗證了把該方法用于制作射表符合系數曲線時，可以提高試驗數據處理效率以及試驗數據的準確度.

符合系數曲線 一元回歸 殘差平方和

在射表編擬的過程中為了盡量消除誤差造成的影響，就引入了修正因子，稱之為符合系數，通過符合系數的修正可以得到標準化射程，進而編制合格的射表.于是在實際射擊過程中，如何較準確的獲得符合系數就是編制射表過程中比較關鍵的一個步驟，通過對數據和現用方法的分析，一元回歸方法及其常用軟件Minitab應該可以在此方面提供一定的幫助.

1 理論方法分析

現使用的獲取符合系數方法是繪制關系曲線，從中讀取非射擊角度的符合系數，制作符合系數曲線的方法有兩種：

一、手工作圖法：將對應的數據點描在采用適當比例尺的圖紙上，各點描好后，用樣條尺將各點擬合成一條光滑的曲線.

二、計算機擬合法：用計算機進行最小二乘擬合，得到擬合方程，繪制曲線.

由于各次試驗的誤差是相互獨立的，并且一般都認同服從正態分布，滿足建立一元回歸模型的原始假定條件，而且回歸分析理論常用的Minitab軟件可以快速完成一元回歸擬合和相應的各項檢驗，所以可以考慮將一元回歸方法應用于符合系數曲線的制作過程中.以榴彈射表為例，某一裝藥號射擊了N個射角，得到N個符合系數FD，FL，射角為θ，假設回歸方程模型

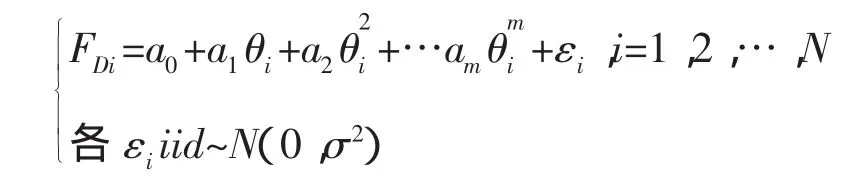
2 實例分析

下面就某型榴彈射表試驗為例計算，其對多個裝藥號和射角進行了射擊試驗.

表1為全裝藥狀態下的符合系數計算的結果，在實際的試驗數據處理過程中使用的是計算機擬合，擬合方程為二次方程

F＝3.1392×10－5θ2－7.6765×10－4θ＋0.9379

表1 全裝藥狀態下的符合系數計算表

運用一元回歸方法對上述的數據進行計算處理，假設模型為一元三次回歸模型.則建立模型為

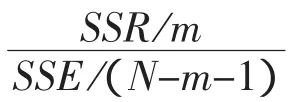
對原擬合的一元二次方程進行各項檢驗，很明顯當α＝0.05時方程顯著，α＝0.025時方程不顯著.R＝0.9524也不如回歸方程擬合的結果理想，模型假設確定合理，說明了原計算機擬合方程假設模型合理，但精度和擬合程度不如回歸方程法，射表編擬計算中更適合使用后者.

另外還對其它數據分別進行了計算和檢驗，其中某型迫彈在使用一元二次的回歸方程 F＝1.4362θ2－3.4891θ＋0.9784時，當取至α＝0.001方程都顯著，且R＝0.9935，擬合程度非常好，模型假設合理.明顯優于其它的假設模型.某型火箭彈在使用一元三次方程的回歸方程

Fθa＝3.500θ3－1.6329θ2＋9.0874θ＋23.6428（取其中之一符合系數說明）時，當取至α＝0.025時方程都顯著，R＝0.9223擬和程度較佳，模型假設合理，優于其它模型.這結果與繪出圖形后觀看曲線的平滑程度以及讀取非試驗角度數據后再次計算的準確程度對比結果是一致的.證明一元回歸方法可以應用于射表編擬過程中的符合系數曲線擬合制作.并且計算過程在Minitab軟件中可以迅速實現，所以此方法快捷方便，適宜實際運用.

3 結束語

上面就一元回歸方法如何應用于射表編擬過程中符合系數曲線的擬合制作問題進行了介紹與驗證，從計算的結果與實際情況的比較來說是準確可行的.其相對于現有方法的優點在于：

1)通過各項檢驗，能更加準確地提供合理精確的回歸方程，從而繪制出更加平滑的符合系數曲線，得到更準確的數據.

2)運用Minitab軟件可以快速準確地進行一元回歸假設和檢驗，并且便于檢查對算.

3)由于各項誤差平方和和殘差檢驗的加入，可以部分解決射角少，基準點相應少的試驗中最小二乘擬合結果出現大偏差的問題.

所以綜上所述，一元回歸方法運用于射表編擬過程中符合系數曲線的擬合制作是可行并且結果是準確可信的.

[1]閆章更，祁載康.射表技術[M].北京：國防工業出版社，2000：196-204.

[2]洪楠，侯軍.MINITAB統計分析教程[M].北京：電子工業出版社，2007：105-120.

[3]周紀薌.回歸分析[M].上海：華東師范大學出版社，1991：1-30.

[4]易正江，畢春麗.Matlab工具在數理統計學中的應用——一元回歸問題的計算機求解法[J].焦作大學學報，2003，17(1)：67-69.

[5]王春光，竇衛國.一元回歸方程的建立和選優[J].內蒙古農牧學院學報，1989，10(1)：150-157.

[6]崔新軍.榴彈射表編擬中符合方法的研究[J].彈道學報，1997，9(2)：72-75.

The App lication of Sim p le Regression M ethod in Producing the Curve of Accommodation Coefficient in Test for Firing Table

LIANGWen－juan1，JIANG Bo2，SA Yan－cheng2
（1.DepartmentofMathematics，Huangshan University，Huangshan Anhui，245041；2.China Huayin Ordnance Test Center，Huayin Shanxi，714200）

Simple regression method is adopted to aim at remedying the shortcomings in making the Curve of Accommodation Coefficient in Test for Firing Table.It is proven that the method will increase the efficiency of processing experiment data and improve the accuracy of experiment data when it is applied in producing the Curve of Accommodation Coefficient in Test for Firing Table.

the Curve of Accommodation Coefficient；simple regression；residual Sum of Squares

O213

A

〔編輯 高海〕

1674－0874（2010）01－0023－03

2009-09-15

黃山學院校級科研基金項目［2006xkjq001］

梁文娟（1982－），女，山西運城人，碩士，助教，研究方向：概率統計.