CJK6140數控車削物理仿真振動模型研究

張少伍，黃 杰，韓 江，錢金明

ZHANG Shao-wu1, HUANG Jie2, HAN Jiang3, QIAN Jin-ming4

（1.銅陵學院 機械工程系，銅陵 244000；2.安徽省白湖閥門廠有限公司，廬江 231508；3.合肥工業大學 機械與汽車工程學院，合肥 230009；4.華強機械股份有限公司，諸暨 311835）

0 引言

隨著制造技術和信息技術的發展，虛擬制造技術實現了虛擬與現實之間的一種映射，其本質是利用計算機支持的仿真技術實現產品設計、制造的優化。虛擬加工過程仿真是虛擬制造的底層關鍵技術，包括數控幾何仿真和物理仿真兩個部分。幾何仿真主要是根據數控程序，仿真工藝系統運動部件的幾何運動軌跡，而物理仿真是數控仿真的核心，它是通過仿真切削過程的動力學特性來揭示加工過程的物理本質，通常物理仿真研究的內容有工件表面質量模型、切削力模型、切削振動模型、切削材料微觀硬度分析模型、切削溫度模型、切削加工誤差模型和切削加工刀具變形模型等等。由于物理仿真切削機理復雜、建模難度大、涉及因素多等客觀原因，目前的研究都還在不斷的進行著。如W.J.Emdres建立了車削力的動態模型和工藝系統的振動模型，Sata等開發的刀具與工件相對振動模型,Zhang和Kapoor建立了考慮加工過程中隨機振動影響的表面粗糙度模型,合肥工業大學劉光復等人提出了同時考慮工件系統和刀具系統的切削顫振模型等等，但這些模型多是對切削加工過程中的某些物理現象做定性分析，目前所做的研究還不能完全滿足生產的要求，尚需作進一步的研究。本文在前人分析的基礎上，對CJK6140數控車削切削振動模型進行研究，為分析刀具振動對加工工件表面質量和切削力的影響打下基礎。

1 數控車削振動的形式

切削加工過程中由于各種干擾因素的存在，切削振動是無法避免的。切削中如有振動發生，不僅會降低工件的表面質量，加劇刀具磨損，破壞機床的連接特性，還會產生刺耳的噪聲，嚴重污染環境。由于車削系統是由機床-工件-刀具構成，在車削加工中存在著各種形式的振動，按照受力類型來分，主要有受迫振動、自由振動、自激振動和混合型振動。

1.1 受迫振動

指切削加工過程中傳動機構的不平衡力，斷續切削的沖擊力，從機床、工件、刀具中產生的脈沖性干擾而引起的振動。

1.2 自由振動

指切屑生成的周期性、斷續切削產生的交變切削力，空運轉時已存在的周期性激振力，刀具碰到工件材質不均的硬點產生的動態力，通過機床系統本身的彈性恢復維持的振動。

1.3 自激振動

又稱顫振，是在工件和刀具之間自發產生的振蕩，是由再生效應、切入效應、切削力下降特性、摩擦效應及振型關聯等原因產生的交變切削力引起的振動。自激振動是由于機床—刀具—工件系統本身造成的。

1.4 混合型振動

綜合了受迫振動和自激振動的變化規律。從車削振動類型分析中可看出，車削加工過程中振動形式多樣，機理復雜，涉及到工藝系統的多方面因素。因此研究車削振動應從總結切削加工中的振動規律入手，重點分析切削系統的振動特點，建立適合仿真系統開發與應用的振動模型。

2 數控車削振動模型分析

在數控車削加工系統中，由于加工過程的振動既影響工件表面質量和機床的穩定性，又影響刀具的磨損，因此對振動的仿真既能預測工件表面粗糙度和刀具壽命，還能確定機床的穩定性極限。而切削力、工件材料、刀具形狀、機床剛度等因素都影響機床的振動，因此對加工系統進行合理簡化以建立既能反映實際情況，又便于分析車削系統振動特性和振動規律的振動模型是必要的。由于數控車削沿工件徑向的振動直接影響切削深度，進而影響切削力的變化和表面粗糙度，再生效應引起的振動也主要出現在工件的徑向,徑向振動對表面粗糙度的影響也最大。因此本文研究切削力引起的徑向振動情況，如圖1所示。

根據前人的研究理論，可將徑向振動的方程采用單自由度二階模型來表達，即：

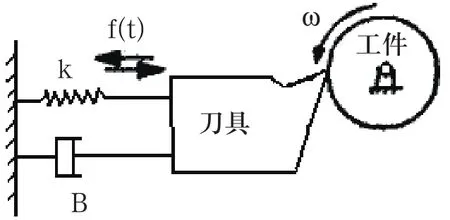
圖1 車削加工振動系統簡化

式中m、B、k是車削仿真模型在徑向的等效質量、阻尼系數和彈簧彈性系數，f(t)為徑向的切削力分量。

3 CJK6140物理仿真振動模型的實驗研究

針對CJK6140物理仿真模型的數學表達式，通過實驗測量振動模型在徑向上的工藝系統參數，包括測量車床系統的靜剛度及阻尼，由此可確定該系統的數學模型。

3.1 車床工藝系統靜剛度的測量

工藝系統的剛度表征工藝系統抵抗變形的能力，一般可用力和在該力作用下的靜態位移的比值來表示，即：

車削加工工藝系統是由機床、刀架、尾座、工件組成的復雜系統，刀具和工件的相對位移是組成工藝系統的各個部件位移的疊加，工藝系統的靜剛度與各個部件靜剛度的關系為：

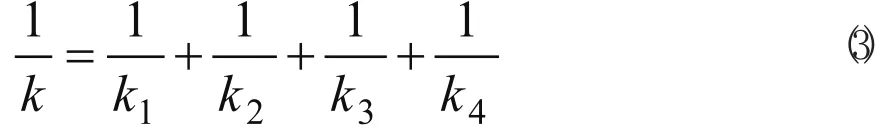
式中k1到k4分別為機床、刀架、尾座和工件的彈性系數。

由于工件材質的不均勻、材料表面的硬度差異及切削點的變化等因素，導致加工工藝系統的剛度是時變的。本文的研究將工藝系統的參數中工件部分參數單獨計算，其他部分由實驗確定的阻尼視為工藝系統阻尼。

按JBIT4368.4-96標準中5.5項靜剛度實驗之規定，采用力傳感器和千分表在CJK6140車床上測得主軸部件、刀架和尾座的位移及剛度如表1所示。

依據上述公式，可得工藝系統的靜剛度為：

K=9.66 N/um

3.2 車床工藝系統阻尼的測量

本文通過測量工藝系統的阻尼比來確定工藝系統的阻尼。由機械振動理論知，振動系統的各參數存在以下關系：

則工藝系統的阻尼B為：

而阻尼比ζ的測量方法有自由振動法和共振法。本文采用共振法。其原理是單自由度系統在受迫振動時，當激振頻率接近系統固有頻率時振動響應顯著增大，根據其幅、頻率響應曲線估算出振動系統的動態參數。共振法分為幅頻曲線分析法、實虛部頻率特性分析法和相頻曲線分析法三種方法。

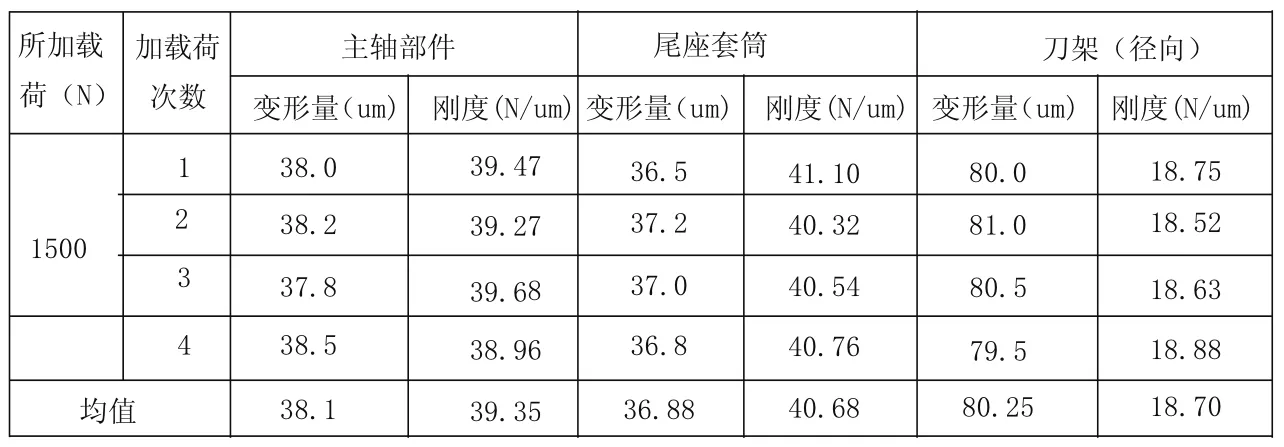
表1 主軸部件、刀架和尾座的剛度統計

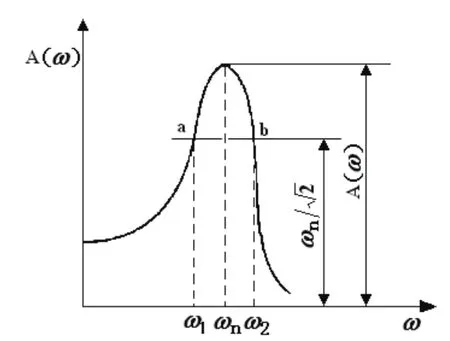
圖2 幅頻曲線分析法求系統的阻尼比

幅頻曲線分析法是對系統施加正弦激勵信號，輸出達到穩定后測量輸出與輸入的幅值比和相位差，逐漸改變激勵信號的頻率，繪制系統的頻幅特性曲線。曲線幅值最大處的頻率就是系統的固有頻率，在固有頻率的處作頻率軸的平行線，相交特性曲線于a、b兩點，這兩點處對應的振動頻率分別為ω1、ω2，如圖2所示，則阻尼比ζ為：

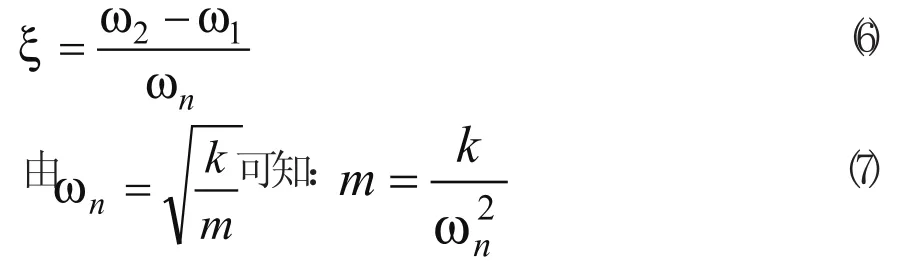
經實驗測量，系統的阻尼比ζ=0.05,B=0.783N.s/um，m=9.985kg

3.3 車削徑向力的確定

在(1)式中的f(t)為激振力的徑向分力，可由兩種方法換算得到。一種是根據車刀的前角、刃傾角、主偏聽偏角等幾何角度，由各車削分力的空間關系計算出；另一種是由車削力的經驗公式直接得到。本文不再討論。

根據實驗數據可得到本CJK6140數控車床徑向切削振動的物理模型為：

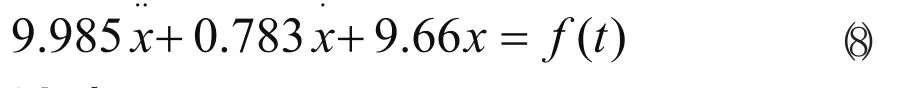
4 結束語

虛擬仿真的目的就是在計算機內部對加工過程進行仿真，并在此基礎上對加工過程進行預測和評價。本文在簡要回顧數控仿真類型的基礎上，分析了數控車削過程中的振動類型，建立了CJK6140數控車削過程中刀具沿工件徑向單自由度振動仿真模型，并通過實驗確定了工藝系統振動模型的系數，為CJK6140數控車床的振動仿真提供了理論依據。

[1] Yu Guo,Wenhe Liao,Xiaosheng Cheng,Liang Liu.SimOpt：A New simulation optimization system based virtual simulation for manufacturing system[J].Simulation Modeling Practice and Theory,2006(14)：577-585.

[2] 陳秀生.基于STEP-NC的數控車削加工仿真關鍵技術研究[D].山東大學,2007.

[3] 黃學梅.虛擬數控車削加工物理仿真系統研究[D].東北大學,2001.

[4] 李紅軍.數控車削表面質量物理仿真與研究[D].南京理工大學,2005.

[5] 張少伍,韓江,胡慧萍.虛擬數控車削加工物理仿真技術研究[J].機械設計與制造,2010(3)：166-168.

[6] 韓志華,羅學科.機床加工過程中的振動實驗研究[J].機床與液壓,2007.35(2)：77-79.

[7] 陳秀生,張承瑞,劉日良,蘭紅波.數控加工物理仿真技術研究[J].組合機床與自動化加工技術,2006,(9)：8-11.