基于遺傳算子的粒子群算法在戰場頻率分配中的應用*

陳自衛 石 雄

(75818部隊1) 廣州 510500)(廣州軍區通信部通信處2) 廣州 510083)

1 引言

在現代戰爭中,為保證部隊能有效獲取作戰信息、保證部隊的合成指揮、保證部隊之間的協同作戰,大量無線電子設備應用于現代戰場,使得現代戰場電磁環境相當復雜。在信息化戰爭中,軍事通信、指揮控制、預警探測、情報偵察、導航定位和武器制導等系統的正常運轉,無不取決于電磁頻譜這一有限的資源。如果缺乏有效的頻譜管理,不同的電子設備間輕則相互干擾,重則喪失作戰能力。為確保部隊正常指揮、打贏現代戰爭就必須保證無線電指揮系統的正常運行。合理使用頻率資源,加強頻率管理就顯得日趨重要[1],這就提出了戰場頻譜管理的課題。因此利用頻率分配技術,合理為戰場環境下各電子設備分配相應的頻率,減少無線通信設備之間的相互干擾,確保無線電通信暢通無阻,是保障現代戰爭指揮順暢的重要手段,也是打贏現代戰爭的重要條件。

頻率分配是優化頻譜利用、提高信道容量、減少干擾的主要手段[2]。目前用于頻率分配的算法有采用滿足頻點間隔結合遺傳算法的頻率優化分配算法、免疫網絡調節算法、免疫遺傳算法、遺傳退火算法、圖的邊著色等等。基于這些算法的研究,國內外各移動通信系統制造商和通信軟件公司都開發出自己的頻率規劃商用軟件。這些商用軟件都具有自己的頻率規劃算法,這些算法的目的都是使網絡干擾減到最小。

本文通過對頻率分配限制性因素的研究,建立了以干擾最小為計算基礎的頻率分配數學模型,將頻率分配問題歸結為整個戰場網絡的干擾評價函數的優化問題,同時采用基于遺傳算子的粒子群算法來對其進行求解,能夠滿足戰場頻率分配高效實時的要求。

2 基于干擾最小的頻率分配模型

在提高頻率資源利用率的諸多方法中,最被廣泛研究和利用的是以頻率復用為基礎的頻率規劃技術。頻率復用就是將同一無線頻率用作不同小區(或扇區)的載頻,這些使用相同的載頻的小區彼此相隔足夠的距離來把同頻(或鄰頻)干擾抑制到允許的范圍以內的方法。頻率復用的技術來提高系統的容量,但不可避免地帶來了不同小區間載波頻率的同頻或鄰頻干擾。

2.1 同頻干擾和鄰頻干擾系數

在一個基站的服務小區內,如果來自其他基站的發射信號足夠強且兩個基站使用相同的頻率,則在該服務小區內就會產生干擾稱為同頻干擾。

設基站A的小區服務半徑為R,基站 A和B之間的距離為L,基站 A和B采用相同的頻率。則A的服務范圍內的移動臺可能受到B的干擾,當載干比C/I≥18db時,認為B對A產生的干擾不足以對A小區內的移動臺的服務質量產生影響,即認為B對A不產生同頻干擾。反之,若C/I＜18db,則認為B對A產生同頻干擾。同理,當基站A和B采用相鄰頻率時,在一定的條件下也會產生鄰頻干擾,在此省略。

在對新基站或新小區進行頻率分配時,由于它們開通運行前不可能從系統中采集這些小區的頻率測量數據,通常可對某小區的同頻干擾系數矩陣和鄰頻干擾系數矩陣進行手工構造,可以根據該小區與其相鄰小區的地理位置關系、這些小區的覆蓋方向以及它們所在區域的地形地物來給定該小區受到其各個相鄰小區的同頻和鄰頻干擾系數,某相鄰小區對該小區可能構成的干擾越大,則分配給此相鄰小區的同頻和鄰頻干擾系數也越大。在此構造小區i對小區j的同頻干擾系數為cij,鄰頻干擾系數為aij。

2.2 基于干擾最小的頻率分配模型

設第i個小區所有載波頻率構成的集合為:

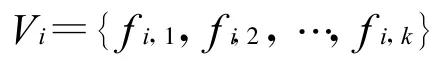
式中,i=1,2,…,n;k為第i個小區的載波數。

設第j個小區所有載波頻率構成的集合為:

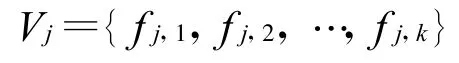
式中,j=1,2,…,n;k為第j個小區的載波數。

設在[t,t+Δ t]時間范圍內,第i個小區受到第j個小區的同頻干擾為,則有 :

式中cij為同頻干擾系數,并有:

其中,l=1,2,…,k。

設在[t,t+Δ t]時間范圍內,第 i個小區受到第j個小區的鄰頻干擾為,則有:

式中,aij為同頻干擾系數,并有:

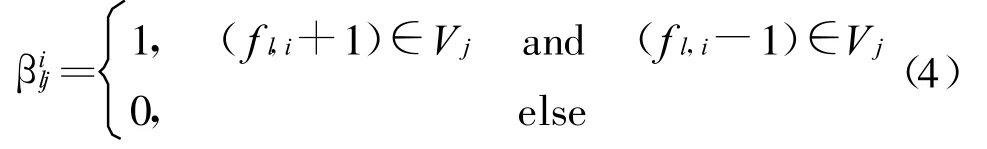
其中,l=1,2,…,k。

在不考慮同頻干擾和鄰頻干擾權重的情況下,可得在[t,t+Δ t]時間范圍內區域中第i個小區受到來自R中其他小區的總的干擾(含同頻和鄰頻)為:

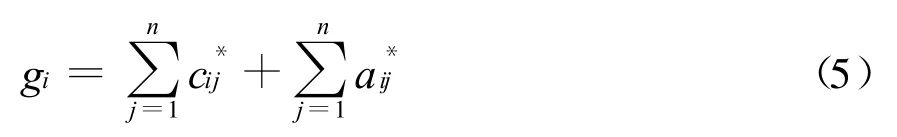
假設對區域R的第i個小區的所有載波的頻率進行重新分配,并將第i個小區的所有載波頻率看作變量,將式(5)看作第i個小區的干擾評價函數,則對第i個小區的所有載波進行頻率規劃的目標即是使式(5)的值達到最小,從而將頻率分配問題轉化為干擾評價函數(在頻率分配中,只需考慮由等待分配的載波頻率所構成的干擾評價函數)的優化問題。

若不考慮頻率分配中的約束條件,通過上述頻率分配的數學模型進一步總結整個區域頻率分配的數學模型為:

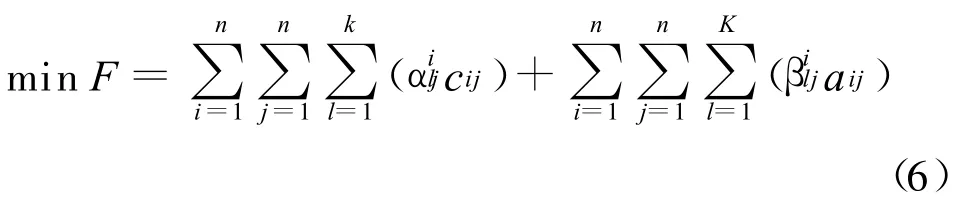
3 基于粒子群的分配算法

3.1 基本粒子群算法

粒子群算法[3～4](Particle Swarm Optimiza-tion,PSO)是一種較新的啟發式搜索算法,最早是由Kenney與Eberhart于1995年提出的,源于對生物群體捕食行為中相互協作的研究。它屬于群智能算法的一種,操作相對簡單,收斂速度快,目前已廣泛應用于函數優化、神經網絡訓練、數據挖掘以及其它的應用領域。

PSO算法的基本思想是:系統首先根據問題的定義域初始化一組隨機解,利用當前的全局最優解和個體最優解對每個粒子進行迭代和更新,并獲得最優解。這個過程可以用下面四個公式來描述

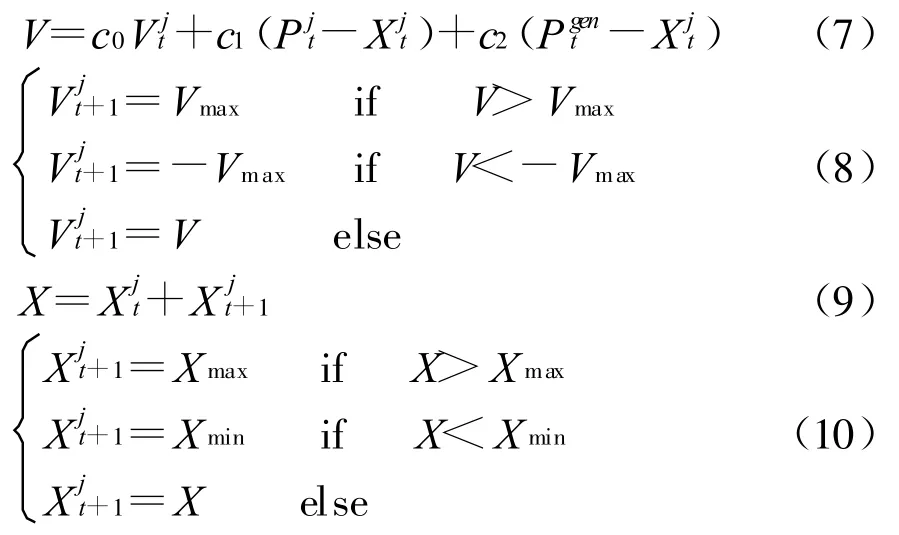
3.2 基于PSO的分配算法

本文采用的PSO算法在步驟上與基本PSO算法相同,所不同的主要有兩個:一是兩者在初始化群體中的操作不同,二是在更新粒子時的思想不同。

3.2.1 初始化群體

在基于遺傳算子的PSO算法中,沒有應用粒子的速度,所以在初始化中不必對速度進行初始化,但要對解的位置結合問題的實際進行編碼。基于遺傳算子的PSO算法不能直接處理解空間上的解變量,需要通過編碼將其表示成類似遺傳算法中基因的形式。具體如下:

對于頻率分配問題,每個染色體長度為 N,相當于要分配頻率的發射機數量。染色體里每個元素值都為整數,對應一個頻率,一種頻率分配為 f=(f1,f2,…,fN)。我們采用符號編碼的方法,即對個體每一個基因座用可用頻率的編號進行編碼。如果有12個頻率可用,那么第一個個體解就是由1到12個正整數組成的。例如,對于長度為6的個體,其解的編碼可能是3-12-11-5-9-3,表示編號為1到6的基站分別采用編號為 3、2、11、5、9和 3的頻率。這樣有以下好處:直觀,便于理解并研究算法的運算過程;易于解碼,因為在基站編號(即頻率分配的解)和個體基因之間有簡單的一一對應關系。

3.2.2 個體更新

基于遺傳算子的PSO算法中的粒子更新策略是此方法的核心,對粒子個體進行更新主要采用了遺傳算法中交叉算子、變異算子和選擇算子等遺傳算子[5],它們的采用避免了有關參數的選擇,也不使用粒子的速度,變得更容易操作,同時也保持了算法的全局搜索能力。以第t代的第i個粒子為例說明粒子更新的操作,步驟如下:

圖1 當Series=‘0110010’時的交叉示意圖

4)計算粒子Q1…Q6的適應度F1…F6,從中選擇適應度最小的粒子Qmin來更新和Pgent。若Qmin的適應度 Fmin＜,則=Qmin;若 Fmin＜,則=Qmin;

4 仿真研究

假設戰場網絡中總共有16個發射機(基站)等待分配頻率,且彼此之間限制關系已知,能使用的頻率范圍為Fmin～Fmax,則我們可以用如下方法來處理問題:

首先,為了解決同小區頻率間隔的限制,我們將Fmin～Fmax分成若干個小的頻段,假定分為48個頻段,分別為 f1,f2,…,f48,然后取 Fl=f1,f17,f33;F2=f2,fl8,f34;…;F16=f16,f32,f48。這樣將16組頻率段分配給不同的小區,則小區內部就不存在頻率間隔的限制了。而鄰頻與同頻的約束就要靠算法使干擾約束數減到最小了。

由于該算法不需要設定交叉和變異概率,其算法的性能參數如下:最大代數100,群體大小60,編碼長度16。所得到的仿真結果如圖2所示。

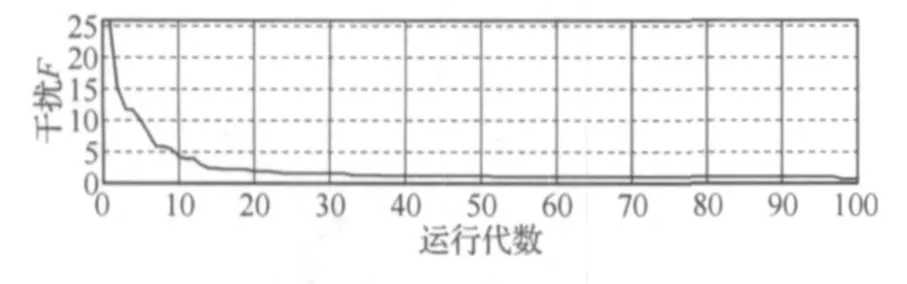
圖2 仿真結果

從圖中可以看出,

1)當算法運行到50代時,整個網絡的干擾已接近最小,可見其收斂速度大大提高;

2)整個網絡的干擾很難完全消除,當運行到100代時,其干擾仍然達不到0;

3)通過交叉、變異和選擇等遺傳算子對編碼的空間進行處理,既增加了解的多樣性,又加快了解的收斂速度,使粒子群算法的搜索效率進一步提高,而且不需要設置更多的參數。

5 結語

如何合理有效地分配戰場各區域所需的頻譜是實現動態頻譜的關鍵技術,戰場電磁頻譜分配模型可以表示為一個優化問題。本文首先提出了基于干擾最小的優化模型,然后運用基于遺傳算子的粒子群算法求解該優化問題,仿真結果表明該算法能更好地實現戰場整個網絡干擾的最小化,在較小進化次數下就能得到整個網絡的理想最優解,驗證了本文所提方法的有效性,從而有效地提高了頻譜分配效率。

[1]希玉久.無線電頻譜資源[J].全球定位系統,2002(5):40～43

[2]王宇飛,蔡立安.無線電頻譜分配新概念[J].艦船電子工程,2007,27(3):17～19

[3]Kennedy J,Eberhart R.Particle swarm optimization[C]//Proc.IEEE Int.Conf.on Neural Networks,1995:1942～1948

[4]高尚,楊靜宇.群智能算法及應用[M].北京:中國水利水電出版社,2006,5

[5]周明,孫樹棟.遺傳算法原理及應用[M].北京:國防工業出版社,1999,7