最小冗余陣旁瓣抑制算法研究

張 璐， 李高鵬， 許榮慶

（哈爾濱工業(yè)大學 電子信息工程系，黑龍江 哈爾濱 150000）

0 引言

近年來, 隨著全球移動通信業(yè)務的迅速發(fā)展。智能天線越來越受到人們廣泛的關注。以往有關智能天線技術的研究多集中于均勻陣。與之相比最小冗余陣可以使天線的陣列孔徑增大，方向性增強，空間分辨率提高。如今已在自適應智能天線[1]和射電天文中的干涉陣等領域中得到廣泛應用[2]。

最小冗余陣MRA（Minimum Redundancy Arrays）的概念最初由Moffet A.T[3]提出。雖然最小冗余陣可以通過減小陣列中現(xiàn)有冗余空間的數(shù)目實現(xiàn)最大空間分辨率，但它的旁瓣電平也隨之升高，在空間濾波時不能有效濾除干擾。因此研究旁瓣峰值抑制算法，選取恰當權值系數(shù)來控制最小冗余陣的旁瓣電平具有實際意義。本文將推導一個算法，將旁瓣區(qū)間劃分為若干個子區(qū)間，利用簡單的迭代技術設計對于最小冗余陣的旁瓣抑制算法。與約束最小二乘旁瓣抑制算法[3]相比，該方法收斂速度快，可控旁瓣個數(shù)多，大大降低了主波束附近的旁瓣電平。且對角度靠近觀察方向的干擾進行抑制時，抗干擾能力增強，信號噪聲干擾比得到提高。

1 最小冗余陣

最小冗余陣屬于稀布陣列中的一種。這里提到的“最小冗余”意在指陣列自相關矩陣R包含最少的重復輸入，即所有陣元間距盡可能地保持兩兩互不相同，當任意兩陣元間距都不相同，則稱這種陣列為零冗余陣。Arsac[4]早在1955年曾提出零冗余線陣的概念，并給出了四種形式的零冗余陣。Bracewell[5]通過大量研究也證實了這一觀點。當陣元數(shù)小于等于 4時，最小冗余陣和零冗余陣是相同的，如下頁圖1所示。

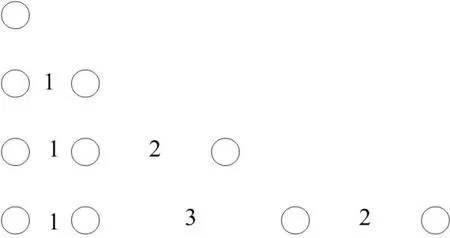
圖1 1到4元零冗余陣

當陣元數(shù)大于4時，陣列將存在一定的冗余度。Leech[6]通過反復研究并采用窮盡枚舉法得出了具有最小冗余度的陣列結構。表1給出了研究結果。

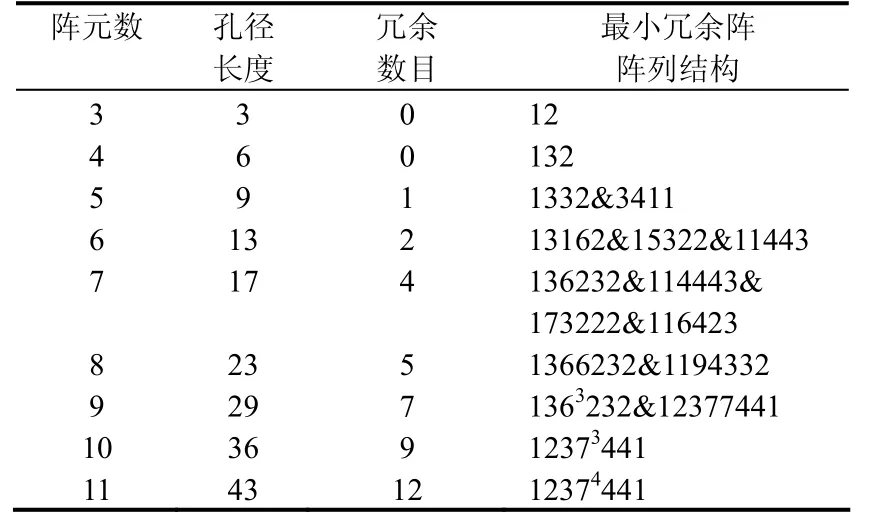
表1 最小冗余陣陣列結構

表1中若用M表示陣元數(shù)，Ma表示孔徑長度，Mr表示冗余數(shù)目。三者關系為：

當冗余數(shù)為0時（零冗余陣列），滿足：

信號噪聲干擾比是陣列天線的一個重要參數(shù)，可以表示為：

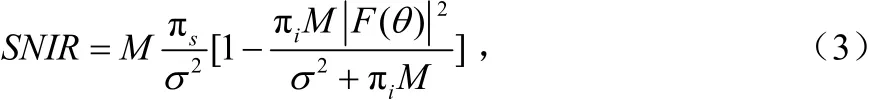
其中，πs為信號在每個陣元處的信號能量，同理πi為干擾在每個陣元處的干擾能量，σ2為噪聲方差，為陣列方向函數(shù)。

圖2為11元最小冗余陣波束方向圖，d為半波長，陣元各向同性，以左邊第一個陣元為參考點，陣元位置為（0,1,3,6,13,20,27,34,38,42,43）。與11元均勻陣相比，最小冗余陣在不增加陣元數(shù)的情況下主瓣寬度減小了17.2°，大大提高了分辨率。但是旁瓣電平較高，為-5.86 dB。可見，高旁瓣不能有效抑制觀察方向附近的干擾，研究最小冗余陣的旁瓣抑制技術具有十分重要的意義。

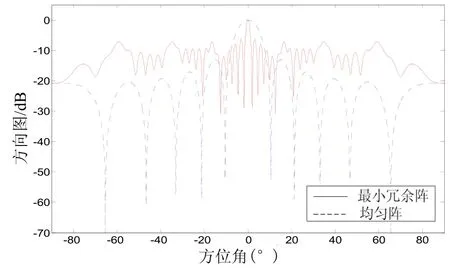
圖2 11元最小冗余陣波束方向圖

2 旁瓣抑制算法原理

假設一個由全向陣元組成的線陣,陣列響應矢量為 v(u)，其中 u =sin(θ)。當方向圖的主響應軸的響應等于1時，方向性為：

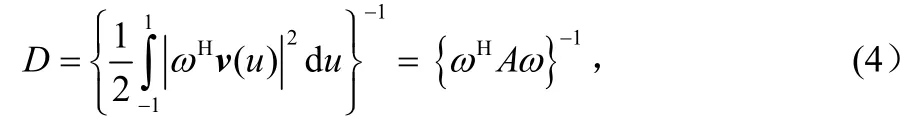
其中，ω為權值矢量。令vT=v(uT)是陣列在陣列調(diào)向上的響應矢量。基本問題是在主軸響應為1的約束條件下，使方向性最大，即：

利用拉格朗日函數(shù)解得：

對于最小冗余陣，希望能夠通過犧牲一些方向性，得到更低的旁瓣。所以可以將u空間分成r個子區(qū)間：Ω1,…, Ωr，并且定義在每個區(qū)間上的理想的波束方向圖。一個典型的理想波束方向圖如圖3所示。

圖3 理想波束方向

假設有一個權值矢量ωd,i，在第i個區(qū)域內(nèi)產(chǎn)生了理想的波束方向圖 Bd,i(u)=。在區(qū)域Ωi內(nèi),理想波束方向圖[8]和由權值矢量ω產(chǎn)生的合成波束方向圖之間的平方誤差為：

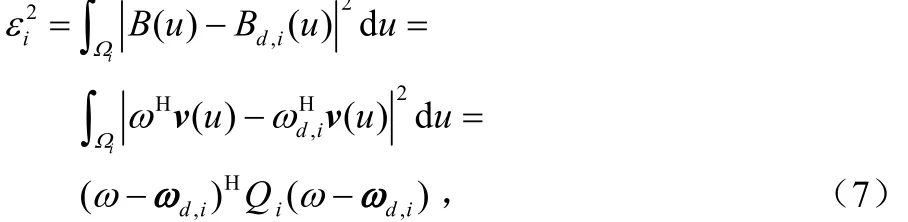
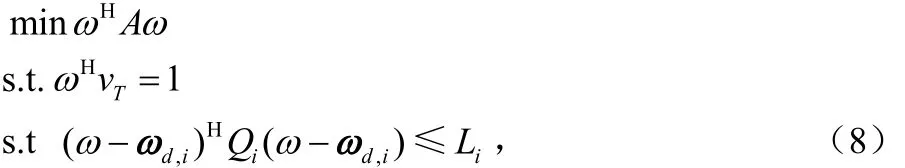
令：

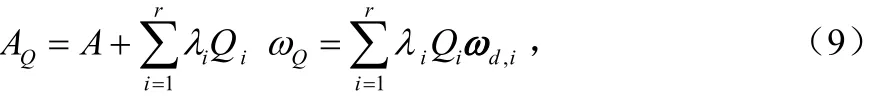
由式（8）、式（9）解得：

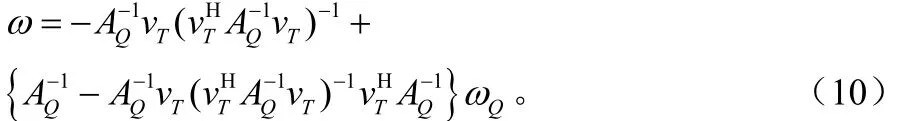
因為僅在旁瓣區(qū)域約束方向圖的誤差，故每個約束子區(qū)間內(nèi)的,diω為零，則式（10）中的第二項就去掉了，權值矢量成為：

在無限小子區(qū)域情況下，方向圖的誤差成為對波束方向圖在旁瓣區(qū)域的每個點上的幅度平方的約束。可以允許的偏差值可以設為最大可允許旁瓣電平，以此來控制旁瓣電平，使其滿足設計要求。在表達式（9）中，iλ為每個子區(qū)間的加載因子。加載因子在理想的低旁瓣方向圖和最大方向性方向圖之間進行平衡。一個迭代過程可以用于調(diào)整加載情況，以實現(xiàn)對旁瓣水平的控制。在每次迭代中，都計算出方向圖的誤差并檢查約束的情況。如果超出了約束，則該區(qū)域?qū)募虞d值將被減小，權值進行更新直到滿足收斂準則，即：

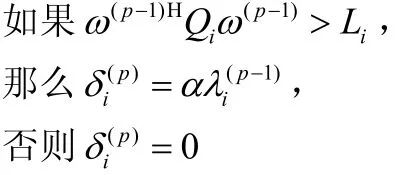
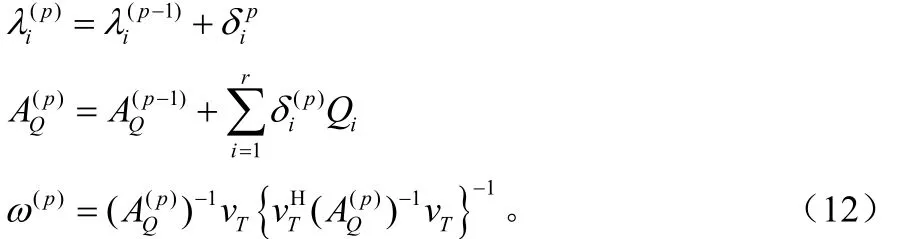
3 實驗仿真結果及分析

應用該算法對 11元最小冗余陣進行旁瓣抑制，觀察方向為0。初始加載量01 0.5 λα==,。由于受自由度控制，最小冗余陣可控旁瓣峰值個數(shù)不大于 1M-,M為陣元個數(shù)，所以這里將對 10個峰值旁瓣（除主瓣以外）進行控制，使其電平保持在-15 dB以下。仿真結果如圖4。

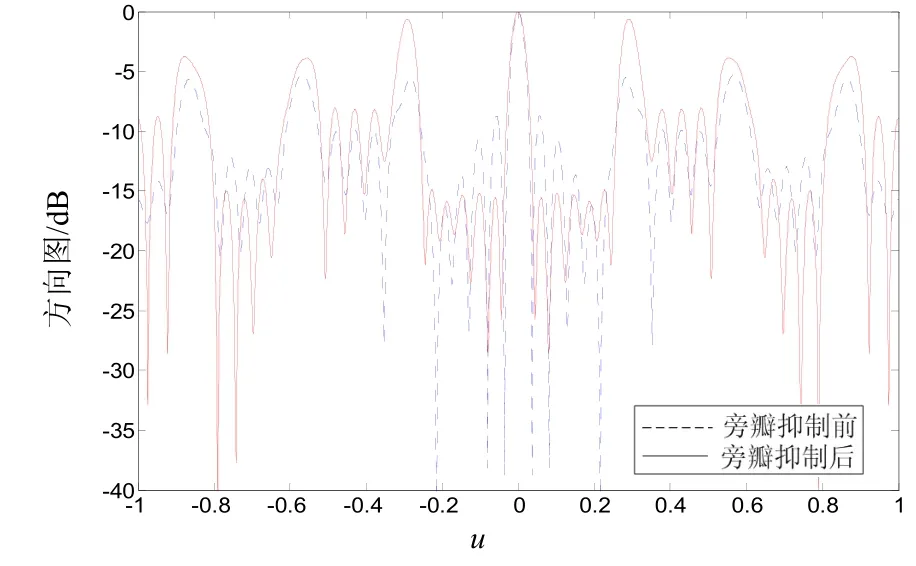
圖4 11元最小冗余陣旁瓣抑制

經(jīng)過11次迭代后，最小冗余陣主瓣寬度由0.072展寬到0.088，主瓣附近的十個旁瓣電平得到了有效控制，控制范圍在 - 0.244～0.244（-14°～14°），電平保持在-15 dB以下。由于最小冗余陣的旁瓣個數(shù)比較多，所以主瓣旁的十個旁瓣被降低后，其余旁瓣電平卻比抑制前升高了，類似于均勻陣中的珊瓣。可見，應用最小冗余陣時，應注意其使用范圍。若超出此范圍時，信號噪聲干擾比較低，且判斷波達方向時易出現(xiàn)誤判。

圖5為等陣元最小冗余陣與均勻陣的對比，由圖可知最小冗余陣的主瓣寬度為 0.122，均勻陣的主瓣寬度為 0.48，遠遠大于最小冗余陣，因此分辨率不如最小冗余陣。

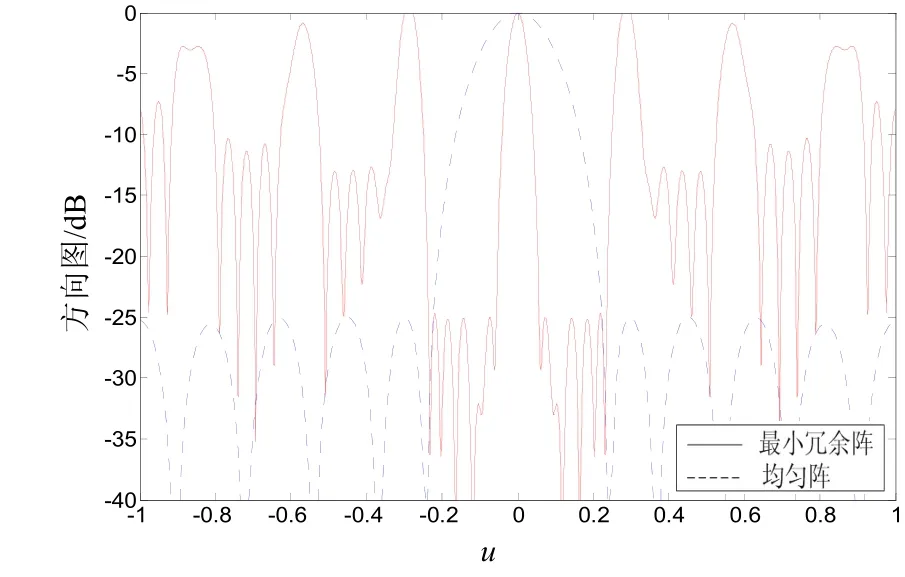
圖5 等陣元數(shù)最小冗余陣與均勻陣

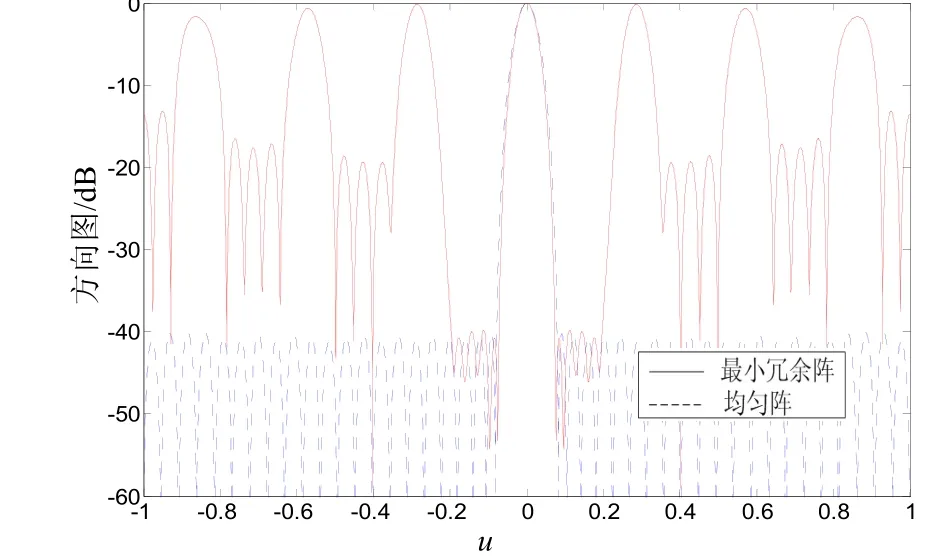
圖6 等孔徑最小冗余陣與均勻陣

圖6為等孔徑最小冗余陣與均勻陣的對比，由圖可知為了獲得相同的陣列孔徑，均勻陣需要44個陣元，而最小冗余陣只需要11個陣元，大大簡化了系統(tǒng)復雜度，降低了系統(tǒng)成本。

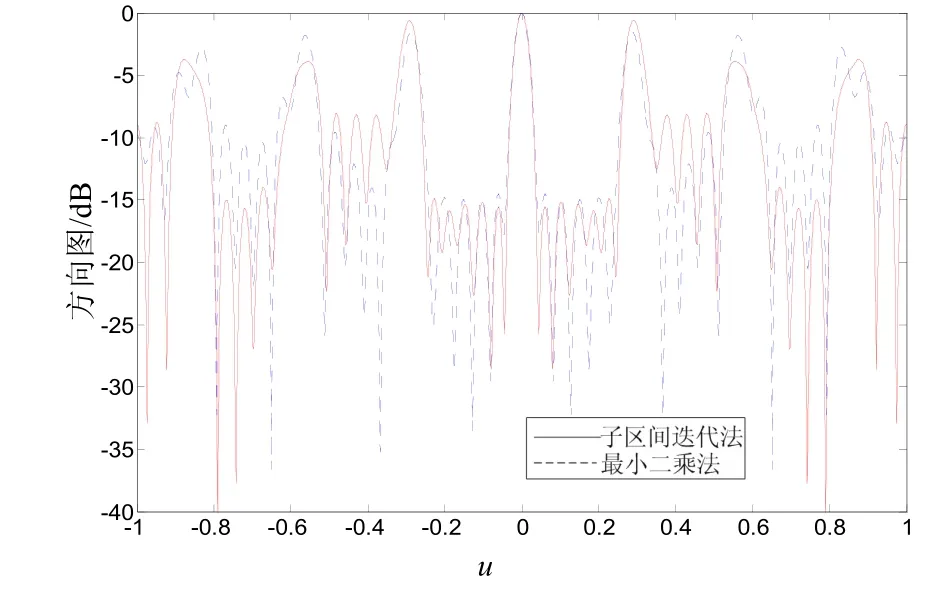
圖7 兩種算法對比

圖7為子區(qū)間迭代算法與約束最小二乘算法的對比，約束最小二乘需要十八次迭代使旁瓣降低到-15 dB以下，而本文提到的子區(qū)間迭代算法只需要十一次迭代就可以滿足要求。另外約束最小二乘可以控制的旁瓣個數(shù)為 8，而后者可以控制10個旁瓣，可控旁瓣個數(shù)比前者多。

圖8對旁瓣抑制前后的信號噪聲干擾比進行仿真對比，可知在 - 1 3.3°～ 1 3.3°范圍內(nèi)，最小冗余陣的SNIR要高于均勻陣，旁瓣降低后最小冗余陣的SNIR得到進一步提高。當干擾位于觀察方向附近±13°時，干擾抑制能力增強。

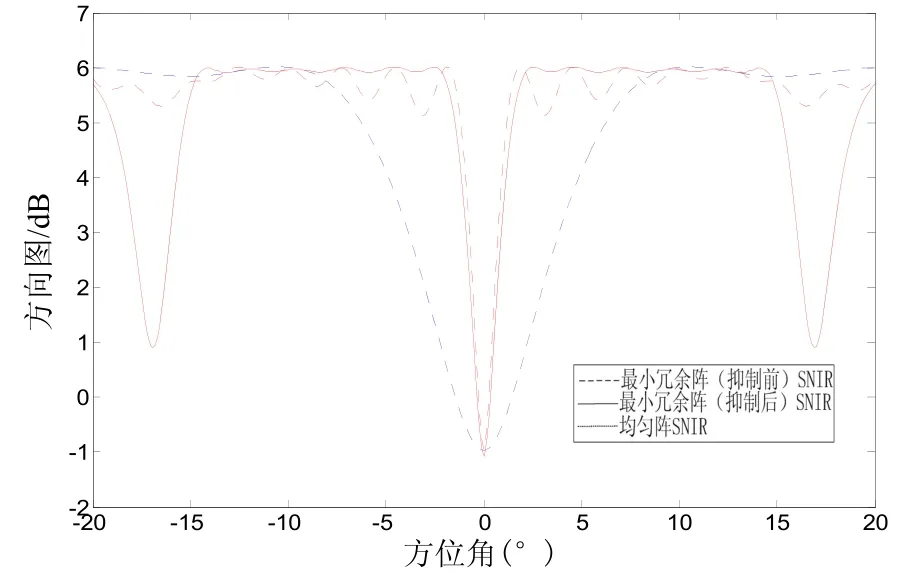
圖8 旁瓣抑制后SNIR對比

4 結語

本文基于子空間迭代算法，提出了一種可以有效控制最小冗余陣旁瓣電平的方法，很好的解決了最小冗余陣旁瓣過高問題，在等陣元的情況下可以獲得更窄的主瓣，在等孔徑的情況下，可以節(jié)省陣元的使用，降低系統(tǒng)成本。仿真結果表明，此方法計算量小，收斂速度快，可控旁瓣個數(shù)多，并且最小冗余陣的旁瓣降低后，能使位于觀察方向附近13±°的干擾得到更好的抑制，提高信號噪聲干擾比。

[1] 王志,趙勇.基于智能天線的TD-SCDMA系統(tǒng)LCS平臺研究[J].通信技術,2007,40(06):27-29.

[2] 李建新.陣列多臺階稀疏技術[J].電子學報,1999,27(03):79-80.

[3] Moffet A T. Minimum Redundancy Linear Arrays[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(02):172-175.

[4] 楊林.陣列天線綜合方法研究[D].哈爾濱:哈爾濱工程大學,2006.

[5] Arsac J. Nouveau Reseau Pour I'observation Radioastronomique De Labrillance Sur Le Soleil a 9350 Mc/s[J]. Compt. Rend.Acad. Scl, 1955(245):942-946.

[6] Bracewell R N.Radio Astronomy Techniques[C]. Berlin Handbuchder Physik, 1962:42-129.

[7] Leech J. On the Representation of 1,2,…,N by Differences[J].London:[s.n.],1956: 160-169.

[8] 李建勇,陳振宇,王明悅,等.適用于WCDMA通信技術的DOA估計方法[J].通信技術,2007,40(12):157-159.