基于遺傳搜索和有限反饋的酉陣設計

何儀周， 程智慧， 王軍生， 雷向勇， 練嵐香

(①北京1481信箱，北京 102442；②北京理工大學，北京 100081)

0 引言

在快衰落瑞麗信道下，差分酉空時調制(DUSTM)適用于無法獲得信道狀態信息(CSI)的情況[1]，發射信號酉陣為正交離散傅立葉變換對角陣——對角線上的元素為復域單位圓上基點相位的整數倍[2]——“頻率系數”，為提升DUSTM性能，文獻[3]提出了基于整數“頻率系數”的分組對角旋轉矩陣的概念。

在慢衰落瑞麗信道下，發射端可完全或部分獲得 CSI：當CSI完全獲得時，發射端可利用特征根進行最優預編碼[4]。由于反饋信道帶寬的限制，發射端無法完全獲得 CSI，故有限反饋預編碼技術應運而生[5]。碼本對于發射/接收端均透明，預編碼結構與DUSTM結構相同。

總之，以上文獻中涉及的酉陣均通過窮舉搜索整型“頻率系數”的方式優化獲得。本文提出了一種基于遺傳算法搜索的實型“頻率系數”方法，仿真結果表明，采用此方法獲得DUSTM及預編碼碼元性能優于整形“頻率系數”碼元，且搜索效率更高。分別表示矩陣的共扼轉置、跡、行列式及F范數。IN表示N×N的單位陣。表示μ均值σ2方差循環高斯變量。A?B表示矩陣A和矩陣B的Kronecker矩陣積。

1 差分酉空時調制(DUSTM)

在準靜態瑞利信道下，假設MIMO系統有tN根發射天線、Nτ接收天線，在2T個時間周期內，信道傳參數近似不變且未知，則接收矩陣表示分組的發射時刻索引，為接收/發射矩陣。信道參數矩陣、噪聲矩陣為獨立同分布(i.i.d)?? ( 0 ,1)隨機變量。

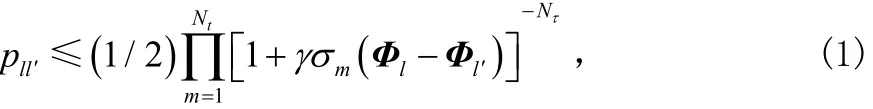
這里，σm( Φl-Φl′)是(Φl-Φl′)的第m個奇異值。碼字的設計準則[2]就是最大化分集積：

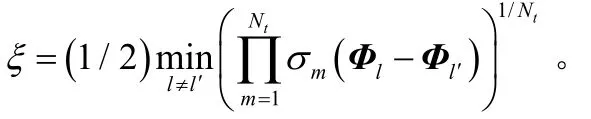
對于 DUSTM[4]而言，基于精確成對錯誤概率的符號錯誤概率(SEP)聯合邊界UBP：

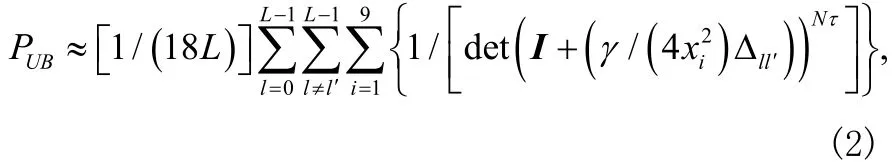
這里，xi=cos(2i-1)π/18。對于DUSTM來說，矩陣集{Φl} 可通過最大化公式(1)或最小化公式(2)獲得。

2 酉預編碼

在信號投送過程中，假設信號星座圖(如QAM等)的信號用（Q信號 { s1,s2,… ,sQ;Q為星座圖容量} 表示）具有單位平均能量，通過與空時碼融合，符號速率 Q /T的發射矩陣 S被變化為適合M根虛擬天線傳送的信號矩陣，最后，信號矩陣S經F預編碼后由 Nt根實際天線發射出去。

① 如果S為一正交空時碼，則FΓ就是w集中保證取極大值時的元素。此時，w集的元素項根據最小“弦距”是w碼本容量)原則進行設計；

② 如果S是VBLAST碼，則FΓ就是w集中保證取極大值時的元素。此時，w集的元素項根據最小“范數間投影距離”

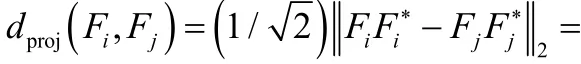
③ 如果S是VBLAST碼，且期望系統容量最大，則FΓ就是w集中保證取極大值時的元素。此時，w集的元素項根據最小“任意成對Fubinistudy距離”進行設計。總之，酉陣預編碼的碼本設計與DUSTM的酉陣碼本設計類似。在一定設計準則下，DUSTM和預編碼都存在著酉陣的結構以及相關參數的優化等問題。

3 酉陣設計

3.1 循環群設計

DUSTM的對角酉陣循環群具有如下形式[2]：

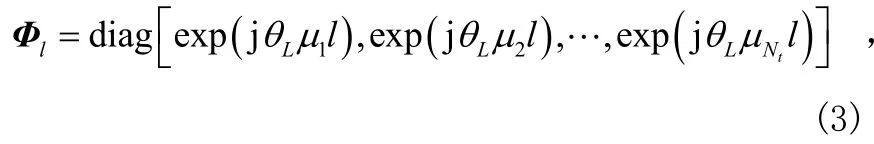
這里，θL=2π/L，l=0,1,…,L -1。公式(3)中的循環碼由Nt和“頻率系數”決定。通過對前面第1節、第2節提及的差分標準進行優化即可得到“頻率系數”μ集。

3.2 循環旋轉設計

循環矩陣乘以分組對角旋轉矩陣RF即可得到循環旋轉矩陣[3]。。旋轉因子0≤ k ＜L與μ可同時進行優化， Nt為偶數。

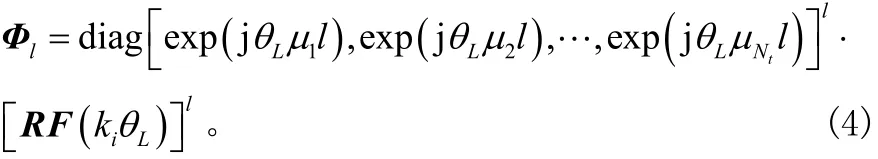
先前的文獻在優化過程中，“頻率”系數采取整形并通過窮舉搜索獲得最優碼本，當 L和tN很大時，運算量相當的龐大，遺傳算法就是解答此問題的鑰匙。

4 遺傳算法

遺傳算法模擬自然選擇和自然遺傳，在每次迭代中保留一組候選解，并按某種指標選取較優的個體，利用遺傳算子(選擇、交叉和變異)對這些個體進行組合，產生新一代的候選解群，重復此過程，直到滿足某種收斂指標為止。

遺傳算法包括：編碼、適應度函數、遺傳算子、運行參數。編碼通過某種編碼機制把對象抽象為由特定符號(二進制串)按一定順序排成的串。適應度函數是個體（解）的好壞的評價標準，適應度函數值越高的個體就越有機會通過交叉或變異等遺產方式傳遞到下一代去。

表1顯示的是當 L =16，32、 Nt=6，8時通過遺傳算法得到的DUSTM分集積，作為對比，根據文獻[3]和文獻[4]采用窮舉整形“頻率”系數搜索得到的分集積也羅列在表中。表2顯示的是基于公式(4)采用遺傳算法得到的L=8,16,32、Nt=4,5,6得到的循環“弦距”，作為對比，基于整形“頻率”系數的窮舉搜索得到的“弦距”也列在表2中。

表1 分別采用遺傳算法和窮舉搜索得到的DUSTM之分集積

表2 分別采用遺傳算法和窮舉搜索得到的酉陣預處理“弦距”

5 仿真結果

圖1顯示的是采用整形“頻率”系數[2-3]窮舉搜索和采用實型“頻率”系數遺傳算法獲得的星座圖符號誤碼率 SEP。仿真環境：瑞麗衰落信道采用Jakes模型，=2.5×103，fd為多普勒頻移， Ts為符號周期， Nt=6 ,Nτ=1 ,L=1 6,32。從圖1可以看出，當SEP =10-5時，遺傳算法碼元相對于循環群碼有0.4dB的增益，相對于循環旋轉碼有0.6dB的增益。

圖1 循環、循環旋轉設計碼元比較

圖2顯示的是 Nt=6,Nτ=1，Alamouti碼元被6×2酉陣預處理的符號誤碼率，相對于 L =8 H和 L =1 6的碼本有3 bit和4 bit的反饋，當 S EP = 1 0-5時，遺傳算法碼元相對于窮舉搜索[6]碼元有0.5dB的增益，窮舉搜索碼元在4 bit反饋時的性能與遺傳算法碼元在3 bit反饋時的性能相當，因此遺傳算法可降低反饋比特數。

6 結語

本文提出了一種采用遺傳算法運用于DUST調制和酉陣預處理的旋轉對角陣設計方法，“頻率”系數采用實型，而非傳統的整數，適用于天線數較大、碼本容量較大的MIMO系統。仿真結果表明，采用此設計方法獲得碼元性能更為優異。

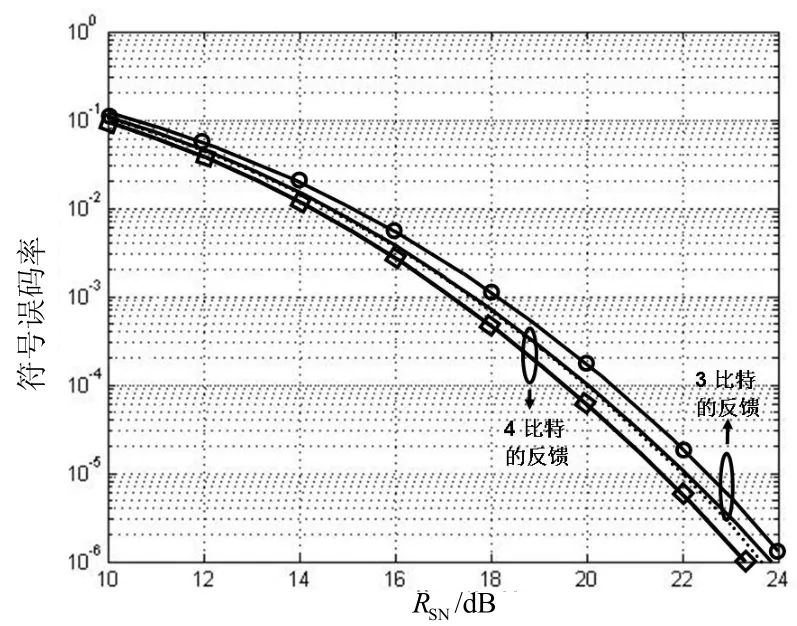
圖2 預處理碼元的性能比較

[1] 張勇,韓力,程智慧,等.Nakagami衰落信道中差分空時分組碼誤比特率分析[J].通信技術,2008,41(10):58-60.

[2] 程智慧,張勇,雷向勇,等. 循環群酉空時碼的優化設計[J].通信技術, 2009,42(12):223-225.

[3] 程智慧,張勇,逄大鵬,等.多發射天線的差分酉空時調制信號星座圖[J].通信技術, 2009,42(10):41-42,45.

[4] Scaglione A, Stoica P, Barbarossa S,et al.Optimal Designs for Space-time Linear Precoders and Decoders[J]. IEEE Trans.Signal Processing,2002,50(05):1051-1064.

[5] Love D J, Heath R W. Limited Feedback Unitary Precoding for Spatial Multiplexing Systems[J].IEEE Trans. Inform.Theory,2005,51(08):2967-2976.

[6] Love D, Heath R J. Limited Feedback Unitary Precoding for Orthogonal Space-time Block Codes[J]. IEEE Trans. Signal Processing, 2005,53(01):64-73.