含時滯與阻尼項的二階半線性微分方程解的振動性

高正暉， 羅李平

(衡陽師范學院 數學系， 湖南 衡陽 421008)

運用Riccati變換和H函數方法，獲得了該方程解的振動性的若干充分條件.

1 問題的引入

考慮一類含時滯與阻尼項的二階半線性微分方程

[r(t)|x′(t)|α-1x′(t)]′+p(t)|x′(t)|α-1x′(t)+
q(t)|x(σ(t))|α-1x(σ(t))=0 (t>T)，

(1)

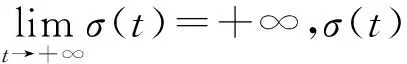
定義方程(1)的一個非平凡解x(t)稱為是振動的,如果它有任意大的零點,否則x(t)稱為是非振動的.

由于在核能物理，氣體動力學和流體力學等方面有著廣泛應用的Emden-Fowler方程

x″(t)+λ(t)|x(t)|α-1x(t)=0 (α>1)，

是一個半線性微分方程，基于半線性微分方程的實際應用背景，吸引了許多學者的研究興趣. A. Elbert[1]首次提出了半線性微分方程的概念，并對半線性微分方程的初值問題解的存在唯一性及解在[0,+∞)上的拓展進行了研究;隨后Horng Jaan Li and Cheh Chih Yeh[2]，Ravi P. Agarwal and S. R. Grace[3]，Arpad Elbert，Kusano Takasi and Tomoyuki Tanigawa[4]，Chen Wendeng and Yu Yuanhong[5]及文獻[6-7]等對二階半線性微分方程解的振動性進行了研究;Qigui Yang and Suisun Cheng[8]，陳目，徐志庭[9]等研究了具有阻尼項的半線性微分方程解的振動性，獲得了若干判定準則.而對具有時滯與阻尼項的二階半線性微分方程解的振動性尚未見相關研究，本文的目的是運用Riccati變換和H函數方法，給出方程(1)解的振動性的若干判定準則.

引理[10]如果X,Y是非負數,那么

Xq+(q-1)Yq≥qXYq-1(q>1)，

其中等號成立當且僅當X=Y.

2 主要結果

令D0={(t,s)|t>s≥t0},D={(t,s)|t≥s≥t0}.

定理假設存在函數H(t,s)∈C1(D,R),h(t,s)∈C(D0,R)和ρ(t)∈C1([T,+∞),(0,+∞)),使得

①H(t,t)=0,H(t,s)>0;

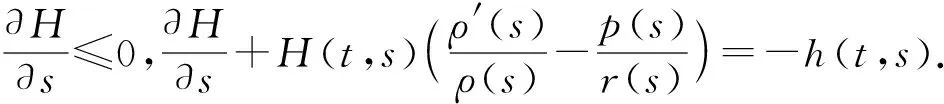
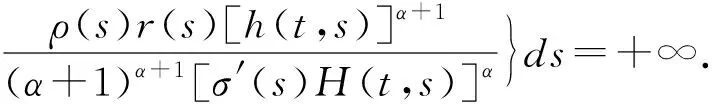
則方程(1)振動.

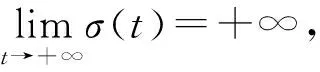
下證x′(t)≥0. 若不然, 對T≥t2,當t≥T時,有x′(t)<0, 令u(t)=-r(t)|x′(t)|α-1x′(t)，則u(t)>0.

u′(t)=-(r(t)|x′(t)|α-1x′(t))′=p(t)|x′(t)·

則有

即

(2)

對方程(2)在[T,t]上積分,得

(3)

令t→+∞并結合條件(H1),有

這與x(t)>0矛盾, 所以x′(t)>0,因此有x″(t)≤0. 從而x′(t)≤x′(σ(t)).

作Riccati變換

則w(t)≥0.

因此,得

ρ(t)q(t)≤-w′(t)+

(4)

將方程(4)的t換為s并兩邊同乘H(t,s),在[T,t]上關于s積分,得

(5)

令

由引理,可得

(6)

由方程(5)(6)可知

(7)

對方程(7)兩邊同除H(t,T)并令t→+∞有

這與條件(H2)矛盾. 定理得證.