基于Longuet-Higgins模型的畸形波模擬方法

劉贊強(qiáng)，張寧川

（大連理工大學(xué)海岸和近海工程國家重點(diǎn)實(shí)驗(yàn)室，大連116024）

海浪是一種復(fù)雜的隨機(jī)過程。19世紀(jì)50年代初皮爾生最先將瑞斯關(guān)于無線電噪音的理論應(yīng)用于海浪，與紐曼等提出了能量譜（海浪譜）的概念，從此利用譜以隨機(jī)過程描述海浪成為主要的研究途徑，至今已提出多種描述海浪的數(shù)值模型，其中最常用的是Longuet-Higgins模型［1-2］。

畸形波是海浪中偶然出現(xiàn)的異常大波，是隨機(jī)波浪的一種特殊現(xiàn)象，對海上建筑物、航行中的船只和近岸結(jié)構(gòu)物等具有強(qiáng)大的破壞性［3-5］。畸形波是一種超大波浪，基本特征是波峰高而陡、波谷淺而平坦。此外，在海洋中形成的具有極大波谷的波浪（“海中深洞”［6］）也被稱為畸形波。目前關(guān)于畸形波的定義還沒有統(tǒng)一。1987 年 Klinting 和 Sand［7］首先提出了畸形波的定義，認(rèn)為畸形波應(yīng)滿足以下條件：（1）Hmax≥2Hs，（2）ηc≥0.65Hmax，（3）Hmax≥2H1且 Hmax≥2H2。其中 Hs為波列的有效波高，Hmax為畸形波的波高，ηc為畸形波的波峰高，H1、H2分別為畸形波前后相鄰波浪的波高。但有學(xué)者［5，8-9］提出，該定義過于苛刻，認(rèn)為（1）和（2）是主要條件，（3）是次要條件。不過，國內(nèi)外研究學(xué)者都一致認(rèn)為畸形波的波高至少為有效波高的2.0倍。本文旨在介紹畸形波的數(shù)值模擬方法，因此采用Hmax≥2Hs這種最簡潔的定義。

近20 a來關(guān)于畸形波的研究日漸增多，但由于畸形波的不可預(yù)測性和實(shí)測資料的匱乏，可靠的分析結(jié)果非常少，發(fā)生機(jī)理和發(fā)生概率還不十分明確。因此有必要對該現(xiàn)象進(jìn)行深入細(xì)致的理論和試驗(yàn)研究。由于天然條件下的現(xiàn)場觀測存在諸多困難，實(shí)驗(yàn)室生成畸形波的技術(shù)還不成熟，數(shù)值模擬成為研究畸形波的一個(gè)重要手段［10］；同時(shí)數(shù)值模擬也為實(shí)驗(yàn)室模擬造波提供了條件。

關(guān)于畸形波的數(shù)值模擬，目前主要有非線性方法和線性方法兩大類。畸形波模擬的非線性方法較多見，大都基于波浪的非線性調(diào)制不穩(wěn)定性（Benjamin-Feir不穩(wěn)定性或邊帶不穩(wěn)定性）。常見的方程有Zakharov方程、非線性薛定諤方程、KDV方程、KP方程和完全非線性方程等［3］。常用方法有高階譜方法（high-order spectral method）［11-13］和邊界積分方法（boundary integral equation）［14］等。非線性方法考慮了波浪的非線性相互作用，貼近真實(shí)的波浪體系，滿足波浪運(yùn)動的控制方程和邊界條件。但是非線性方法較繁瑣，計(jì)算量大，不易于工程應(yīng)用，且很難應(yīng)用于實(shí)驗(yàn)室模擬造波。

相比之下，基于Longuet-Higgins模型的線性疊加方法較簡便，易于工程應(yīng)用，是海洋工程、港口海岸工程以及相關(guān)工程領(lǐng)域進(jìn)行波浪要素統(tǒng)計(jì)、波浪荷載計(jì)算和結(jié)構(gòu)安全設(shè)計(jì)等最常用的方法，同時(shí)也是實(shí)驗(yàn)室模擬造波的常用方法。在實(shí)驗(yàn)室中，如果完全采用波浪的隨機(jī)性模擬畸形波，根據(jù)波高的Rayleigh分布，大約3 000個(gè)波浪中才會出現(xiàn)一個(gè)畸形波；由于實(shí)驗(yàn)設(shè)備所限，該方法不被實(shí)驗(yàn)室所采用，因此首先通過數(shù)值模擬的方法在有限的時(shí)間和空間內(nèi)產(chǎn)生畸形波，為實(shí)驗(yàn)室模擬提供條件。

本文將介紹幾種線性模擬畸形波的模型：相位調(diào)制模型（部分組成波初相位相同模型［15］，相位角分布范圍調(diào)制模型），相位調(diào)制加聚焦模型［13］，隨機(jī)波加瞬態(tài)波模型［16］和一種新的數(shù)值模型——改進(jìn)的相位調(diào)制模型。其中，除隨機(jī)波加瞬態(tài)波模型外，采取的都是調(diào)節(jié)組成波隨機(jī)初相位的方法；除相位調(diào)制模型外，其余方法均可以實(shí)現(xiàn)畸形波的定時(shí)定點(diǎn)生成，同時(shí)隨機(jī)波加瞬態(tài)波模型和改進(jìn)的相位調(diào)制模型還可以更加精確地實(shí)現(xiàn)畸形波大小的可調(diào)節(jié)生成。

本文將就以上幾種模型分別進(jìn)行闡述，旨在說明線性疊加法模擬畸形波的原理、方法，不考慮模擬參數(shù)、波浪的非線性等對模擬結(jié)果的影響，僅限于二維情況。

1 隨機(jī)波浪的模擬

基于Longuet-Higgins模型可實(shí)現(xiàn)常規(guī)隨機(jī)波浪（不含畸形波的隨機(jī)波浪）的模擬［1］。某一固定點(diǎn)的波面方程可以由無數(shù)個(gè)隨機(jī)的余弦波線性疊加來描述

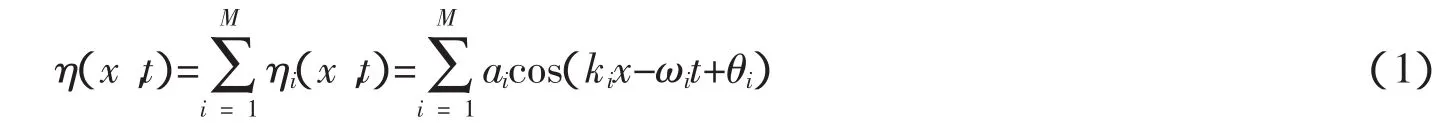
式中：M為組成波數(shù)；ηi（x，t）為第i個(gè)組成波的波動水面相對于靜水面的瞬時(shí)高度；ai為第i個(gè)組成波的振幅；ki和ωi分別為第i個(gè)組成波的波數(shù)和圓頻率；θi為第i個(gè)組成波的初相位，常規(guī)隨機(jī)波浪模擬時(shí)，組成波的初相位是在（0，2π）內(nèi)均勻分布的隨機(jī)數(shù)。

2 畸形波數(shù)值模擬模型

本文的數(shù)值條件為：目標(biāo)譜采用JONSWAP譜［17］，模擬參數(shù)取有效波高Hs=2.0 m，水深d=40 m，譜峰升高因子γ=3.3，譜峰周期Tp=7.0 s，組成波數(shù)M=100，高頻處截?cái)囝l率為4倍的譜峰頻率。

2.1 相位調(diào)制模型

為了實(shí)現(xiàn)隨機(jī)波浪序列中模擬產(chǎn)生畸形波，需要集中組成波的能量。通常情況下可通過調(diào)整部分組成波初相位的方法來實(shí)現(xiàn)，相位角的分布代表著波浪能量集中的程度。

2.1.1 部分組成波初相位相同模型

黃國興［15］采用部分組成波初相位相同的辦法，令M個(gè)隨機(jī)初相位的1/9（比如：第9、18…99個(gè)）、1/8、1/7、1/6、1/5、1/4、1/3取同一個(gè)值，模擬波列包含約2 600個(gè)波浪，考察模擬波列中最大波高的變化。

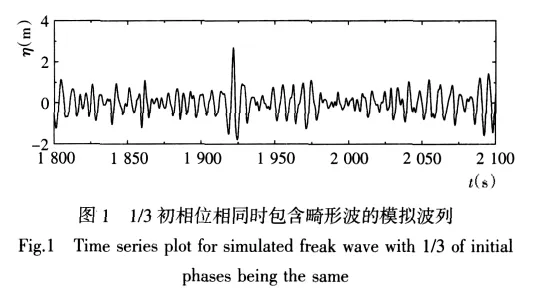
模擬發(fā)現(xiàn)，隨著相同初相位的組成波比例的增加，波列中的最大波高逐漸增大，滿足畸形波判斷標(biāo)準(zhǔn)的幾率增高。當(dāng)有1/3組成波初相位相同時(shí)，模擬波列中發(fā)現(xiàn)了畸形波。圖1為1/3組成波初相位相同時(shí)，包含畸形波的模擬波列，其中Hmax/H1/3=2.21＞2.0。

2.1.2 相位角分布范圍調(diào)制模型

如前所述，相位角的分布代表著波浪能量的集中程度。若縮小組成波的相位角分布范圍，則組成波的能量分布就相對集中，隨機(jī)波列中畸形波發(fā)生的概率將會增加。

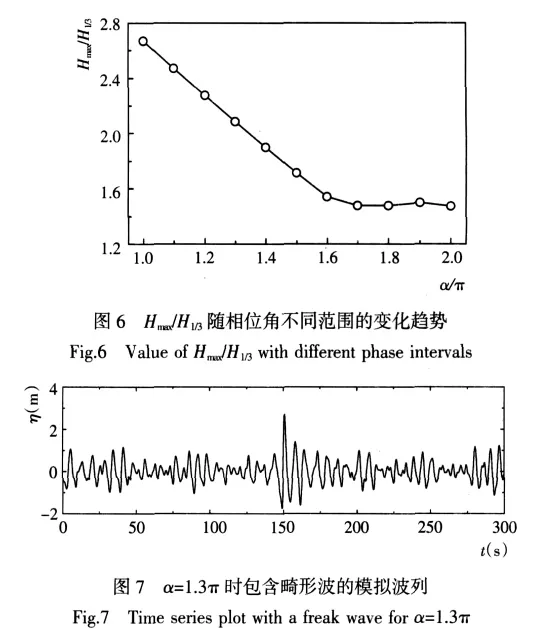
令組成波的初相位在（0，α）內(nèi)均勻隨機(jī)分布，0≤α≤2π，α取不同值時(shí)，波浪能量會有不同程度的集中。圖2給出了α取不同值時(shí)，模擬波列中Hmax/H1/3的值隨相位角分布范圍的變化趨勢。從圖2中可以看出，相位角分布范圍越窄，Hmax/H1/3的值越大，波浪能量集中越明顯。當(dāng)α等于1.3π時(shí)，模擬波列中Hmax/H1/3=2.01＞2.0，已經(jīng)出現(xiàn)了畸形波，其結(jié)果見圖3。

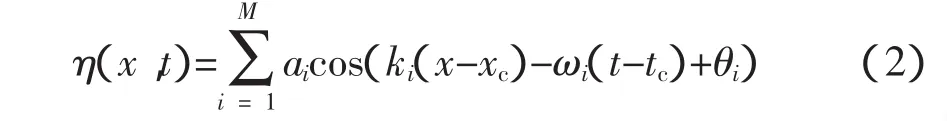
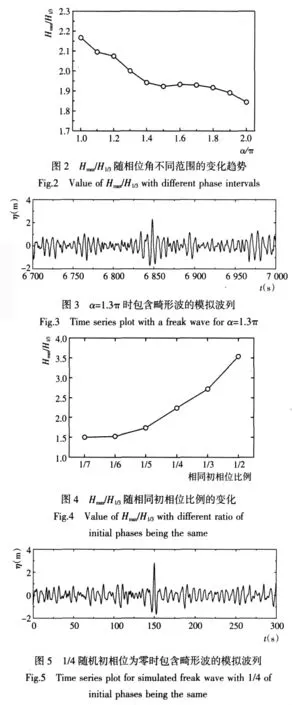
式中：xc和tc分別為波浪聚焦的位置和時(shí)刻。如果θi為 0，則式（2）演變?yōu)樗矐B(tài)波面方程；如果 θi為（0，2π）內(nèi)均勻分布的隨機(jī)數(shù)，則式（2）仍然為隨機(jī)波浪的模擬方程。為實(shí)現(xiàn)波浪能量的聚焦，如前所述，則需要通過調(diào)制組成波的隨機(jī)初相位的方法，來促使波浪能量的集中。

調(diào)制組成波隨機(jī)初相位的方法包括調(diào)整部分組成波初相位相同和調(diào)整相位角分布范圍2種。設(shè)聚焦位置xc=0 m，tc=150 s。為了簡潔，本文只給出波面時(shí)間序列。

（1）調(diào)整部分組成波初相位相同。

調(diào)整部分組成波的初相位為零，則該模型演變?yōu)樗矐B(tài)波加隨機(jī)波的組合模型，通過給定瞬態(tài)波列的生成時(shí)間tc和地點(diǎn)xc，達(dá)到控制生成畸形波的目的。依次令 M 個(gè)隨機(jī)初相位的 1/7、1/6、1/5、1/4、1/3、1/2為零，計(jì)算模擬波列中Hmax/H1/3的值，其結(jié)果見圖4。由圖4可見，隨著相同初相位比例的增加，波列中Hmax/H1/3的值逐漸增大，在1/4組成波初相位為零時(shí)，Hmax/H1/3=2.23＞2.0，模擬波列中出現(xiàn)了畸形波（圖 5）。

另外，實(shí)驗(yàn)室模擬聚焦波常采用的方法是將波面方程（1）中的初相位 θi取值為 θi=-kixc+ωitc+2πs，其中 s=0，±1，±2，……，則波面方程（1）演變?yōu)榉匠蹋?）的形式，其方法是一樣的。

（2）調(diào)整相位角分布范圍。

縮小組成波的隨機(jī)初相位分布范圍，則組成波的能量分布就相對集中。各組成波的初始相位角分布在不同范圍內(nèi)時(shí)，模擬波列中Hmax/H1/3的變化如圖6所示。從圖6可以看出，相位角范圍越小，波浪能量在聚焦點(diǎn)越集中，模擬波列中Hmax/H1/3的值越大。圖7給出了α=1.3π時(shí)包含畸形波的模擬波列，其中Hmax/H1/3=2.23＞2.0。

上述方法提高了畸形波的模擬效率，實(shí)現(xiàn)了畸形波的定時(shí)定點(diǎn)生成，但是不能細(xì)微地調(diào)控畸形波的生

以上2種模擬方法都具有很強(qiáng)的隨機(jī)性，不易控制畸形波的生成大小、生成時(shí)間和生成地點(diǎn)，模擬效率很低。如果將其結(jié)合起來，即縮小相位角的分布范圍并使部分初相位相同，可提高畸形波的發(fā)生概率，但依舊不能準(zhǔn)確地控制畸形波的生成大小、生成時(shí)間和生成地點(diǎn)，因此不做計(jì)算。為提高畸形波的模擬效率，給實(shí)驗(yàn)室模擬畸形波提供條件，須在有限的空間和時(shí)間內(nèi)模擬出有效的畸形波。

2.2相位調(diào)制加聚焦模型

為實(shí)現(xiàn)波浪能量的定時(shí)定點(diǎn)聚焦，Zhao［14］借鑒瞬態(tài)波面方程的形式，將波面方程（1）改寫為成大小。

2.3 隨機(jī)波加瞬態(tài)波模型

Kriebel［16］提出了一個(gè)快速有效地模擬畸形波的方法：假設(shè)一個(gè)包含畸形波的波列由隨機(jī)波列和瞬態(tài)波列組合而成，將整個(gè)波列的能量分為P1和P2兩部分，P1用來產(chǎn)生隨機(jī)波列，P2用來產(chǎn)生瞬態(tài)波列。此時(shí)，波面方程（1）可表示為

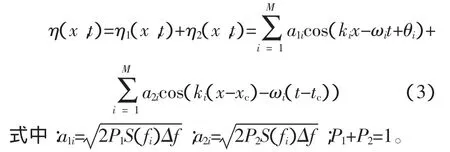
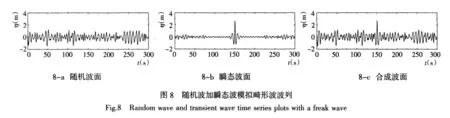
圖 8給出了一個(gè)模擬示例，P1=0.8，P2=0.2，合成波列中Hmax/H1/3=2.01＞2.0，滿足畸形波的定義。

隨機(jī)波加瞬態(tài)波模型模擬畸形波具有較高的效率，實(shí)現(xiàn)了畸形波的定時(shí)定點(diǎn)生成；通過改變波浪能量的分配，可以細(xì)微地調(diào)控畸形波的生成大小。顯然，模擬波列中Hmax/H1/3的值受瞬態(tài)波所占能量P2的影響；如果P2太小，瞬態(tài)波起不到應(yīng)有的作用，模擬波列中很難形成畸形波；如果P2過大，將會影響整個(gè)模擬波列的波浪統(tǒng)計(jì)特性。下面介紹一種新的數(shù)值模擬方法——改進(jìn)的相位調(diào)制方法，該方法既實(shí)現(xiàn)了畸形波的定時(shí)定點(diǎn)和定量生成，又保持了波浪序列的統(tǒng)計(jì)特性。

2.4 改進(jìn)的相位調(diào)制模型

根據(jù)預(yù)先設(shè)定的波浪聚焦位置來調(diào)制各組成波的隨機(jī)初相位，從而達(dá)到定時(shí)定點(diǎn)生成畸形波的目的。設(shè)在位置x=xc，時(shí)刻t=tc時(shí)發(fā)生畸形波，根據(jù)畸形波是單個(gè)大波峰的特點(diǎn)來調(diào)制θi，使部分組成波在x=xc、t=tc時(shí)ηi為正，則在此疊加的波高會增大。

令組成波數(shù)M=M1+M2，波面方程（1）可以寫為

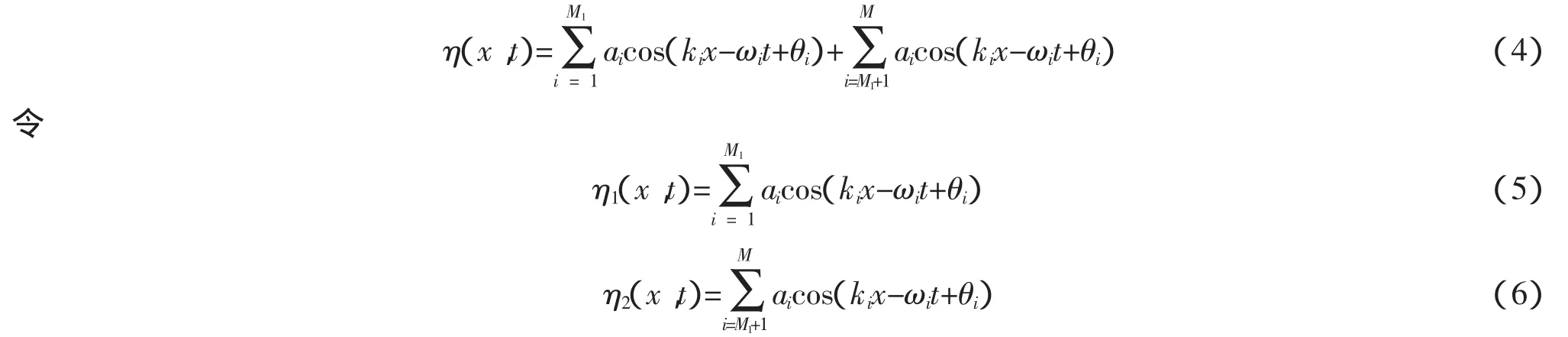
在此令后M2個(gè)組成波的合成波面η2（x，t）在預(yù)定位置處聚焦出現(xiàn)大波，需要調(diào)制后M2個(gè)組成波的初相位θi，使ηi（xc，tc）＞0。

（1）當(dāng)kixc-ωitc＜0時(shí)，令整數(shù)N=int［（kixc-ωitc）/2π］，易知N＜0，式（6）可以寫為

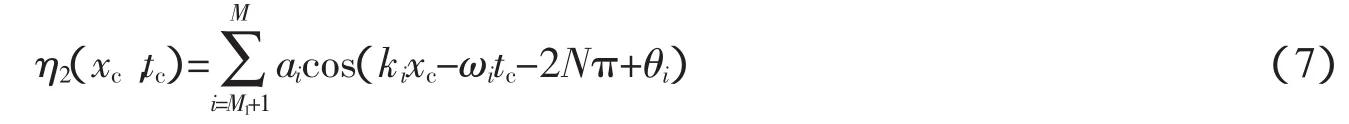
調(diào)制θi（0＜θi＜2π），使，這樣cos（kixc-ωitc-2Nπ+θi）＞0，亦即此時(shí)ηi（xc，tc）＞0，η2（xc，tc）＞0。

由于-2π＜kixc-ωitc-2Nπ＜0，θi按照下述條件取值：當(dāng)，θi在此區(qū)間內(nèi)均勻隨機(jī)選取；當(dāng)，θi在此區(qū)間內(nèi)均勻隨機(jī)選取；當(dāng)，θi在此區(qū)間內(nèi)均勻隨機(jī)選取；當(dāng)，θi在此區(qū)間內(nèi)均勻隨機(jī)選取。

（2）當(dāng)kixc-ωitc≥0時(shí)，令整數(shù)N=int［（kixc-ωitc）/2π］，易知N≥0，式（6）可以寫為

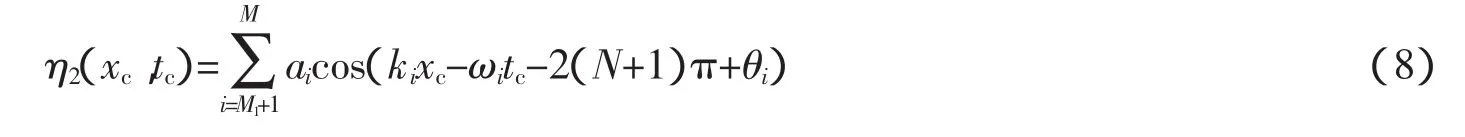
調(diào)制θi（0＜θi＜2π），使，這樣cos（kixc-ωitc-2（N+1）π+θi）＞0，亦即ηi（xc，tc）＞0，η2（xc，tc）＞0；θi的確定方法與情況1中所述的相同，不再贅述。

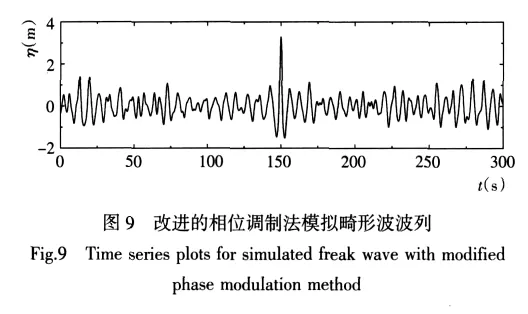
圖9給出了應(yīng)用改進(jìn)的相位調(diào)制法模擬得到的包含畸形波的波列，其中Hmax/H1/3=2.38＞2.0。

該方法具有極高的模擬效率。通過改變調(diào)制波浪的數(shù)目，可以精確地調(diào)控聚焦處波浪的大小，從而實(shí)現(xiàn)了畸形波的可調(diào)控生成。

值得一提的是，如果調(diào)制部分組成波的隨機(jī)初相位使ηi為負(fù)，則波浪在聚焦處就形成了“海中深洞”。

3 結(jié)論

本文介紹了幾種模擬畸形波的數(shù)值模型，概述了各模型的原理和方法，并簡單比較了其優(yōu)缺點(diǎn)。相位調(diào)制模型雖然能夠模擬出畸形波，但是模擬效率很低，不能控制畸形波的生成時(shí)間和生成地點(diǎn)，也不易控制畸形波的大小；相位調(diào)制加聚焦模型較相位調(diào)制模型有了改進(jìn)，提高了模擬效率，實(shí)現(xiàn)了畸形波的定時(shí)定點(diǎn)生成，但對畸形波的大小不能進(jìn)行細(xì)微的調(diào)控；隨機(jī)波加瞬態(tài)波模型和改進(jìn)的相位調(diào)制模型，具有很高的模擬效率，不但實(shí)現(xiàn)了畸形波的定時(shí)定點(diǎn)生成，同時(shí)還實(shí)現(xiàn)了畸形波尺度的細(xì)微調(diào)控生成，方法最優(yōu)。應(yīng)用本文介紹的方法，可推廣到實(shí)驗(yàn)室模擬產(chǎn)生畸形波，進(jìn)而為研究畸形波對結(jié)構(gòu)物的作用奠定了基礎(chǔ)。

［1］Longuet-Higgins M S.On the statistical distribution of the heights of sea waves［J］.Journal of Marine Research，1952，11（3）：245-266.

［2］俞聿修.隨機(jī)波浪及其工程應(yīng)用：三版［M］.大連：大連理工大學(xué)出版社，2003.

［3］Kharif C，Pelinovsk Y E.Physical mechanisms of the rogue wave phenomenon［J］.European Journal of mechanics B/Fluids，2003，22（6）：603-634.

［4］Kharif C，Pelinovsk Y E，Slunyaev A.Rogue waves in the ocean［M］.Berlin：Springer，2009.

［5］Dysthe K，Krogstad H E，Müller P.Oceanic rogue waves［J］.Annual Review of Fluid Mechanics，2008，40（1）：287-310.

［6］Stansell P.Distributions of extreme wave，crest and trough heights measured in the North Sea［J］.Ocean Engineering，2005，32（8-9）：1 015-1 036.

［7］Klinting P，Sand S.Analysis of prototype freak waves［C］//Darlymple R.Proc.Spec.Conf.Near-shore Hydrodynamics.New York：ASCE，1987.

［8］Clauss G F，Schmittner C E，Hennig J.Systematically Varied Rogue Wave Sequences for the Experimental Investigation of Extreme Structure Behavior［J］.Journal of Offshore Mechanics and Arctic Engineering，2008，130（2）：021009.1-021009.11.

［9］Petrova P，Soares C G.Maximum wave crest and height statistics of irregular and abnormal waves in an offshore basin［J］.Applied Ocean Research，2008，30（2）：144-152.

［10］張運(yùn)秋.深水畸形波的數(shù)值模擬研究［D］.大連：大連理工大學(xué)，2008.

［11］Dommermuth D G，Yue D K P.A high-order spectral method for the study of nonlinear gravity waves［J］.Journal of Fluid Mechanics，1987，184：267-288.

［12］Ducrozet G，Bonnefoy F，Le Touzé D，et al.3-D HOS simulations of extreme waves in open seas［J］.Nat.Hazards Earth Syst.Sci.，2007，7（1）：109-122.

［13］Zhao X Z，Sun Z C，Liang S X.Efficient Focusing Models for Generation of Freak Waves［J］.China Ocean Engineering，2009，23（3）：429-440.

［14］Kharif C，Giovanangeli J P，Touboul J，et al.Influence of wind on extreme wave events：experimental and numerical approaches［J］.Journal of Fluid Mechanics，2008，594：209-247.

［15］黃國興.畸形波的模擬方法及基本特性研究［D］.大連：大連理工大學(xué)，2002.

［16］Kriebel D L.Efficient simulation of extreme waves in a random sea［C］//Olagnon M，Athanassoulis G，Rogue Waves.Brest：Ifremer，2000.

［17］Goda Y.A comparative review on the functional forms of directional wave spectrum［J］.Coastal Engineering Journal，1999，41（1）：1-20.